Luma AIでも使われる「NeRF」の論文を徹底解説したい（論文output)

NeRF:Representing Scenes as Neural Radiance Fields for View Synthesis

この説明は下記の論文からお送りいたします。

間違えているところもあるかもしれません。適宜質問や修正をもらいたいです。

0.忙しい方へ

少し硬い説明をすると

NeRFは、視点依存の放射輝度と体積密度を出力する5次元の連続関数として複雑なシーンをの新しいビューを合成し表現します。

• 新しい視点の合成において先行研究を上回る結果を達成しています。

簡単な説明

3Dのシーンを写真から再構築する新しい技術です。想像してみてください、あなたがたくさんの写真を撮って、それらをコンピュータに入れると、コンピュータがそれらの写真から3Dの世界を作り出すんです。それがNeRFのやることです。

1. 論文NeRF:Representing Scenes as Neural Radiance Fields for View Synthesis解説

1.0 要約

NeRFはNeural Radiance Fieldsの略です。
シーンを5次元の連続関数として表現し、ニューラルネットワークでこれを学習することで、複雑な実世界のシーンのビューシンセシスが可能SOTAを塗り替えた論文です。

1.1 導入

この論文では、５次元のデータ表現を使用して、静的シーンの放射輝度を効率的に捉え、レンダリングエラーを減少させる新しいビュー合成技術について述べています。具体的には、この方法では３次元空間の位置（x, y, z）と２次元の視線方向（θ, φ）を入力として使用し、この位置から特定の方向に放射される光の輝度とボリューム密度を出力する。多層のニューラルネットワークを通じて、これらの入力座標から正確な出力を予測するように学習し、ビュー合成の精度を高めることができます。

• 多層のニューラルネットワーク：以降,MLPと呼びます。

• レンダリング:データを処理もしくは演算することで画像や映像・テキストなどを表示させること
• ビュー合成:既存の画像から新しい視点の画像を生成するプロセス
• ボリューム密度:物理的なものは光を通さないのでそこにものがあると言う確率が高くなる。遮蔽の程度だとおもってください。
• 静的なシーン:時間によって変化しないシーン。いわゆる動いてるものはできませんよという意味。
• 放射輝度:光の放射面上の一点の明るさ (輝き) を表します.

1.2 関連研究

• コンピュータビジョンでは三次元空間の位置から符号付き距離などの暗黙的な形状データを使用してMLPの重みにシーンをエンコードする方法が増えて入るが三角形メッシュやボクセルグリッドといった離散的な表現を用いる技術と同じレベルの忠実さで複雑なジオメトリーを持つリアルなシーンを再現することができていない
• 明示的な形状データ:形状の物理的な輪郭や表面を直接的な数学的データ構造で表します。（ポリゴンメッシュやボクセルグリッドなど）
• 暗黙的な形状データ:、形状に関する直接的な情報を持たず、ある数学的関数によって間接的に形状を定義している。（符号付き距離関数など）
• 位置の符号付き距離:ある点が表面からどれだけ離れているか（そしてその点が表面の内側か外側か）を示す値

1.2.1 Neural 3D 形状表現

• xyz座標を符号付き距離関数に変換する研究[15][32]
• occupancy fieldsの最適化：[11], [27]
• ShapeNet：[3]
• 2D画像を使用したニューラル暗黙の形状表現の最適化：[29], [42]

これらの技術は複雑で高解像度の幾何学、形状を表現できる可能性がありますが幾何学的複雑さが低い単純な形状に限定されており、その結果、レンダリングが過度に滑らかになってしまいます。

1.2.2 ビューの合成とイメージベースのレンダリング

ライトフィールドサンプル補間技術：[21], [5], [7]
拡散外観を持つメッシュベース表現：[48]
視点依存の外観を持つメッシュベース表現：[2], [8], [49]
微分可能なラスタライザー：[4], [10], [23], [25]
パストレーサー：[22], [30]
観測画像から直接色付けされるボクセルグリッド：[19], [40], [45]
入力画像からサンプル化された体積表現を予測するための深層ネットワーク：[9], [13], [17], [28], [33], [43], [46], [52]
レンダリングのためのアルファ合成：[34]
サンプル化されたボクセルグリッドと組み合わせた畳み込みニューラルネットワーク（CNN）：[41], [24]
これらの体積測定技術は、新しいビュー合成で目覚ましい結果を達成しましたが、高解像度の画像にスケーリングする能力は、離散サンプリングによる時間と空間の複雑さの低さによって基本的に制限されます。
高解像度の画像をレンダリングするには、3D 空間のより細かいサンプリングが必要です。
あとでurlを追加します....。

1.3 NeRF

1.3.1 NeRFの概要

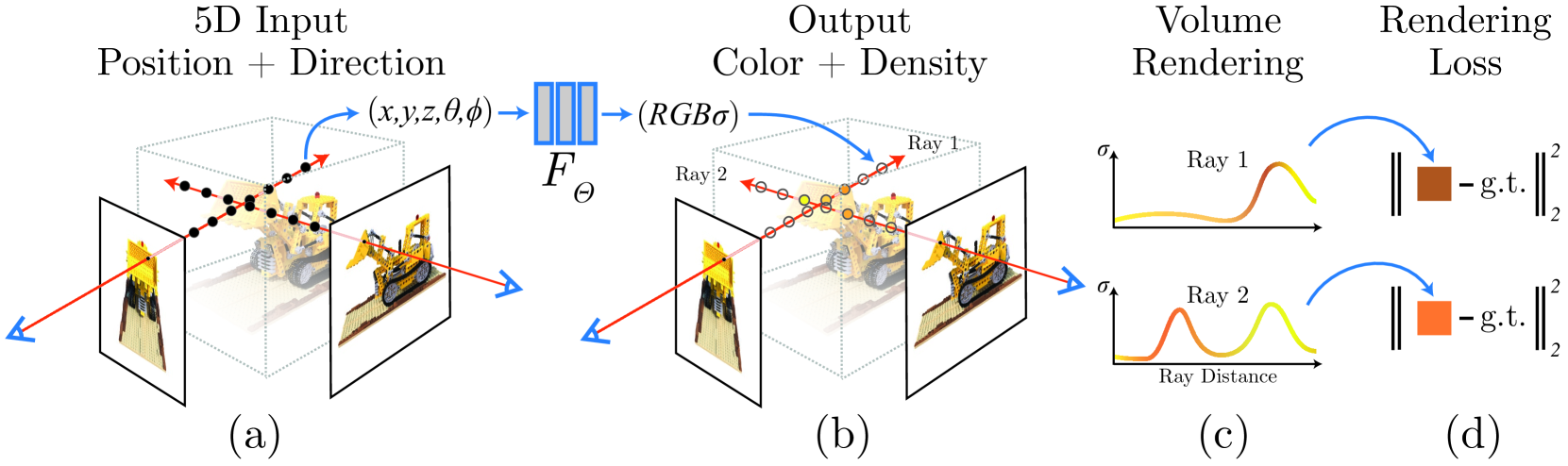
この画像は提案手法のシーン表現と差分可能なレンダリングの手順を示したものです。

(a) 与えられたカメラ位置から、シーン内にレイを射出する。

(b) レイに沿って一定間隔でサンプリング点(絵の中の○）を取り、その位置と方向をニューラルネットワークに入力する。ネットワークからはその点の色と密度が出力される。

(c) ボリュームレンダリングの手法を用いて、出力された色と密度からレイに沿った色を合成する。

(d) 合成された画像と ground truth の画像との誤差を算出する。

(e) この誤差からネットワークのパラメータを更新する。

このように、体積レンダリングに基づく差分可能なレンダリングを行うことで、ニューラルネットワークからなるシーン表現を最適化できるということを示しています。
なので(a)はNeRFの入力を作成するための準備です。
これに

• レイ(ray):コンピュータグラフィックスにおいて、カメラからシーン内のある点へ向かう光線のこと。レンダリングの際には、カメラから画像平面上の各ピクセルに対応するレイを飛ばし、そのレイとシーンの交点を求めて色を計算します。

1.3.2 与えられたカメラ位置から、シーン内にレイを射出する

シーン内にレイを射出するとは、仮想的にカメラからシーン内へ向かうレイを生成することを意味しています。撮影した実画像そのものにレイを照射するのではなく、学習やレンダリングのためにシーン内のレイを計算していると考えてください。

赤い線がレイ

具体的には以下のような処理です:

1. 仮想カメラの位置とパラメータ(視野角等)を設定する

2. そのカメラの画像平面上の各ピクセルに対応するように、カメラからシーン内の点へ向かうレイを計算する

3. レイの方向と距離に基づき、レイ上の複数の点をサンプリングする

4. それらのサンプル点の位置をニューラルネットワークに入力し、色や密度を取得する

5. レイに沿って色を合成して画像をレンダリングする

カメラのポーズ(位置と方向)は以下の2通りの方法で算出されています。

1. 合成データの場合

• カメラのポーズはレンダリング時に指定されたパラメータが既知なので、その情報を直接利用できる

1. 実画像の場合

• COLMAPというStructure from Motion (SfM)ソフトウェアを使用して、複数の入力画像からカメラのポーズを推定
• 画像の特徴点マッチングと幾何学的制約を利用して最適化を繰り返し、カメラの姿勢を自動推定

論文の5.3節の実装の詳細で、実画像の場合はCOLMAPを使ってカメラの内部パラメータ、ポーズ、シーンの境界を推定していると記されている。

つまり、合成データでは既知の情報を使い、実画像ではCOLMAPによるSfM解析によってカメラポーズを推定していると言えます。NeRF自体はカメラポーズを推定する手法ではなく、与えられたポーズ情報を利用しています。
このように、あくまで仮想的なレイを生成し、それを用いてシーンをレンダリングしているという意味です。実画像に直接レイを照射することはありません。

仮想カメラの位置とパラメータの設定は、この手法では2通りの方法が述べられています。

1つ目は、実際にシーンを撮影した時のカメラの位置とパラメータを使用する方法です。

論文では、実画像の撮影に使用したカメラの位置、視線方向、視野角などの情報を与えることができると仮定しています

• structure from motionから画像を撮影したカメラの位置、視線方向、視野角を推定

この情報がある場合は、そのまま同じカメラパラメータを仮想カメラに適用できます。

2つ目は、レンダリングの際に任意のカメラパラメータを設定する方法です。

画像の合成実験では、シーンを取り囲むような位置に仮想カメラを配置しています(図1など)。

この場合は、自由にカメラの位置や視線方向を設定可能です。

つまり、シーンの学習時と、レンダリング時でカメラパラメータの設定方法が異なります。

質問コーナ

Q：

• 2つ目の任意とはランダムな値という意味ですか？

A:
いいえ、「任意のカメラパラメータを設定する」とは、ランダムな値を設定することではなく、理想的な視点でシーンをレンダリングしたい位置にカメラを配置する、という意味です。
例えば、シーンの学習時には限られた視点からの画像しか使えないことが多いですが、レンダリング時には視点を自由に動かしてシーンを観察したいとします。
その場合、レンダリング時には学習時とは異なる視点のカメラ位置・方向を設定できる、ということを表現したかったのです。

つまり「任意のパラメータ」というのは、シーンを最適な角度から見たいという目的に応じて、柔軟にカメラパラメータを指定できる、という意味です。

ランダムに設定するのではなく、レンダリングしたい視点に応じて適切なパラメータを設定する、という意味

Q:
撮影した画像にレイを当てるのですか？
A:
実画像からレイを生成するときの処理を説明している箇所です。

具体的な手順は以下のようになります:

• 入力として実カメラで撮影したRGB画像を用意する。
• この画像の各ピクセル座標p = (x,y) に対応する、シーン内へ向かうレイを計算する。という流れです。

Q：
位置とパラメータ(視野角等)は何系ですか？
A:
入力とされる３次元空間の位置（x, y, z）と２次元の視線方向（θ, φ）です。

• 3次元空間の位置(x, y, z)を表現するために、デカルト座標系(直交座標系)が使用されています。

デカルト座標系では、3次元空間の任意の点Pを、3つの数値(x, y, z)の組で表現します。

• x:左右方向の位置

• y:上下方向の位置

• z:奥行き方向の位置

• 2次元の視線方向を表すのに、球面座標系のθ(仰角)とφ(方位角)が使用されています。
  

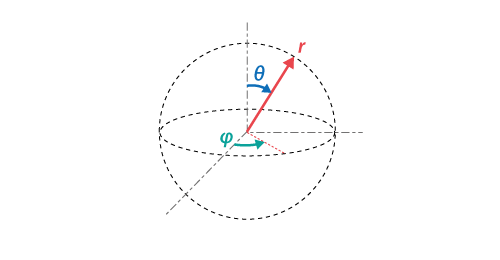
球面座標系では、視線ベクトルの方向dは以下のようにθ(0 ≤ θ ≤ π)とφ(0 ≤ φ < 2π)の2つの角度で表現できます。

• θ: z軸からの仰角。水平方向からの角度。
• φ: x軸からの方位角。水平面内での角度。

(x,y,z): これは画像上のピクセルに対応するシーン中の3次元空間の点を指します。ただし、これはピクセルが「指す」3次元空間の点を意味し、必ずしもピクセルが位置する絶対座標を直接表すわけではありません。NeRFはレイトレーシングのようなアプローチを使って、カメラから出る光線（ray）がシーンのどの点を通過するかを決定します。各ピクセルから出る光線がシーン内のどの点を通過するかは、カメラのパラメータ（位置、向き）とピクセルの位置に基づいて計算されます。

(θ,ϕ): これはカメラの向きを表す角度であり、その3次元点を観測しているカメラの向きを指します。通常、これらの角度はカメラ自体の姿勢に基づいており、その場所から見たシーンのどの方向を向いているか（カメラの視線方向）を示します。これはカメラがワールド座標系内でどのように位置しているか（カメラの位置と姿勢）に基づいて計算されます。

　画像の引用
3Dモデルの基本① ～3DCGの世界は座標で管理されている～
極座標系

1.3.3 ニューラルネットワークによるレイサンプリング点の色と密度の出力

先程の各レイに沿って、等間隔でサンプリング点を決定します。

そして、サンプリング点の3D座標(x, y, z)、視線方向(θ, φ)を取り出す。

そしてボリュームレンダリングを使用しシーンを通過するあらゆる光線の色をレンダリングします 。

C(r) = \int_{t_n}^{t_f} T(t) \sigma(r(t)) c(r(t), d) \, dt

• カメラレイrに沿った放射輝度の積分C(r)

• r(t): レイrにおけるパラメトリック方程式。
  r(t) = o + td (o はレイの原点、t はレイに沿ったパラメータ、d はレイの方向の単位ベクトルです。)

• tn, tf: レイの近平面と遠平面におけるパラメータ

• T(t): r(tn)からr(t)までの透過率(transmittance)

• c(r(t), d): 位置r(t)から視線方向dに対する放射輝度

• σ(r(t)): 位置r(t)におけるボリューム密度
  T(t)を詳しく説明します。
  体積レンダリングにおける透過率（Transmittance）を表しています。この透過率は、カメラから光線が進むにつれて、光が媒体内の粒子によってどの程度吸収されるかを示す指標です。

T(t) = \exp \left( -\int_{t_n}^{t} \sigma(r(s)) \, ds \right)

• σ(r(s)): 位置r(s)におけるボリューム密度
• exp は指数関数で、ここでは吸収の影響を表現するために使われます。

expの中の積分はレイが始点からパラメータ t に至るまでの間に遭遇する体積密度の積分です。この積分値は、その経路に沿ってどれだけの光が吸収されたかの累積を表します。

したがって、光の量がどれだけ減少するかを指数的に計算することで、最終的に点 t に到達する光の割合を与えます。透過率は、0から1の間の値を取り、1に近いほど光が少なく吸収され、0に近いほど光が多く吸収されることを意味します。

通常この積分には決定論的求積法が使用されます。

決定論的求積法は離散化されたボクセル グリッドのレンダリングに使用されますがこれでMLPを使用するとサンプル点が常に同じ場所にしかないならば、ニューラルネットワークは常に同じ位置でのみ学習や評価を行うことになり、その結果、シーンを表現する解像度が固定されたサンプルの位置に依存してしまいます。

• 決定論的求積法:数値積分の手法の一つであり、関数の積分値を計算するために決定論的な手順を用いる方法（いわゆる普通の積分）

よって
下の数式のような積分を数値的に評価するためのサンプリング手法を使用します。
stratified sampling approach

t_i \sim U\left(t_n + \frac{i-1}{N}(t_f - t_n), t_n + \frac{i}{N}(t_f - t_n)\right)

ここで、

• t_n: レイの近平面におけるパラメータ
• t_f: レイの遠平面におけるパラメータ
• N: サンプルの総数
• i: サンプルインデックス (1からN)
• U[]: 一様分布
  つまり、レイの範囲 [t_n, t_f] を N 個に分割し、各分割区間から一様確率でサンプリング点 t_i を選択しています。

これにより、レイ全体にわたってほぼ均等にサンプリング点が分布されることになります。

定義されているストラティファイドサンプリングが使用される主な理由は以下の2つです。

1. ネットワーク入力の連続性を保つため

2. レイ全体にわたって均等なサンプリングを実現するため

決定論的サンプリングでは、サンプル位置が完全に固定されてしまいます。これではネットワークが連続関数を学習することが困難になります。

そこで、ストラティファイドサンプリングでは、各間隔からランダムサンプリングすることで、連続な入力空間でネットワークが学習できるようになります。

また、各区間から均等にサンプリングすることで、レイの手前側や奥側などに偏らず、レイ全体をカバーするサンプルを得られます。

つまり、連続関数の学習と、レイに沿った均質なサンプリングの両方の目的を満たすsampling方策だから、この式が使用されています。

このサンプリングからレイrに沿った放射輝度Ĉ(r)を計算する式です。

\hat{C}(r) = \sum_{i=1}^{N} T_i (1 - \exp(-\sigma_i \delta_i)) c_i

Ti: i番目のサンプル点までの透過率
σi: i番目点でのボリューム密度
δi: 隣接サンプル点間の距離
ci: i番目点での放射輝度
つまり、各サンプル点のボリューム密度σiと放射輝度ciを透過率Tiで重み付けして合成しています。

式(3)が使用される理由は以下の2つです。

ボリュームレンダリングの標準的な計算方法
ネットワーク出力の差分計算が可能
この式はボリュームレンダリングにおける標準的な輝度合成の計算プロセスです。
ここから式３は結局アルファブレンドに帰着します。
これでレンダリングが完了します。

---

Q: 式（１）と（３）の違いはなんですか？

A：式(1)と式(3)の違いは以下の通りです。

• 式(1)は、レイに沿った連続的な輝度積分を表す理論式です。

• 式(3)は、離散的なサンプル点からの輝度合成を表す数値計算の式です。

式(1)のC(r)は、連続的な積分でレイの輝度を理論的に表現しています。

一方、式(3)のĈ(r)は、離散的なサンプル点からの合成によってC(r)を数値的に見積もる式です。

つまり、式(1)が連続的な理論式であるのに対し、式(3)は実際の計算手順を表した離散的な式という違いがあります。

式(3)は、連続積分の式(1)を満たすように、ニューラルネットワークの出力を学習するために使用されています。

式（1）が体積密度関数に関する積分を表すのに対し、式（3）は実際の色の蓄積を計算するための積分であり、その過程で式（1）で計算される体積密度の情報を使用しています。両方の式は、3Dシーンから2D画像を合成するためのボリュームレンダリングプロセスにおいて重要です。​
Q: なぜアルファブレンドに帰着するのですか？
A:　まず、Ĉ(r)の計算において、δi = ti+1 - ti は隣接するサンプル点間の距離を表しています。

そして、このĈ(r)を計算する関数は、(ci, σi) の組からレイの色を合成する関数ですが、これは自明に微分可能であると述べています。

つまり、Ĉ(r)をニューラルネットワークの出力に対して適用することで、誤差逆伝播が可能になる、ということです。

さらに、σi = 1 - exp(-σiδi)とおくと、この計算は标准的なアルファ合成に帰着することも示しています。

アルファ合成は透明度αを用いて色をブレンドする手法ですが、σiがαiに対応するとみなせます。

つまり、提案手法のレンダリング方程式は微分可能かつアルファ合成に等価であることを示しているのです。

---

NeRFの最適化

先程説明したコンポーネントは最先端の品質を達成するには十分ではないことがわかりました。
高解像度の複雑なシーンを表現できるようにするための 2 つの改善を導入します。

• 1 つ目は、MLP による高周波関数の表現を支援する入力座標の位置エンコーディング
• 2 つ目は、この高周波表現を効率的にサンプリングできるようにする階層サンプリング

Positional encoding

ニューラルネットワークが連続したデータを扱う際に、入力としての各位置の情報を改善するためのテクニックです。
入力の3D位置xと視線方向dに対して次のようなエンコーディングを適用しています。

γ(p) = (sin(20πp), cos(20πp), ..., sin(2L-1πp), cos(2L-1πp))

ここで、pは入力座標の値(x,y,zまたは視線方向θ,φの要素)で、Lは正弦関数の最大周波数を決定します。

このγに入力座標を通すことで、高い周波数成分を含むようにマッピングされます。

これにより、ニューラルネットワークは高周波数な関数を表現しやすくなり、シーンの高周波数な細部まで学習できるようになります。

位置エンコーディングはネットワークの入力層でのみ適用され、その後の層では通常のベクトルが入力となります。

論文では位置xにL=10、視線方向dにL=4のエンコーディングを適用しています。
transformerにも使用されています。

位置エンコーディングを取り除くと、高周波のジオメトリとテクスチャを表現するモデルの能力が大幅に低下し、結果としてオーバースムースな外観になります。

Hierarchical volume sampling

ヒエラルキカルボリュームサンプリング（Hierarchical Volume Sampling）は、NeRF（Neural Radiance Fields）において効率的にレンダリングを行うための手法です。基本的なアイデアは、シーン全体を単一のニューラルネットワークで表現するのではなく、2つのネットワーク（「粗い（coarse）」と「細かい（fine）」）を使用して、サンプルの割り当てをレンダリングの最終的な効果に応じて動的に調整することです。

まず、「粗い」ネットワークを使って層化サンプリングにより
Nc個の位置をサンプリングし、それらの位置でネットワークを評価します。このステップでは、式（2）と式（3）が使用されます。この「粗い」ネットワークの出力に基づいて、各レイに沿ってより情報に基づいたサンプリングを行います。つまり、体積内の関連する部分にサンプルを偏りがちに配置します。

hat{C}_c(r) = \sum_{i=1}^{N_c} w_i c_i, \quad \text{where} \quad w_i = T_i(1 - \exp(-\sigma_i \delta_i))

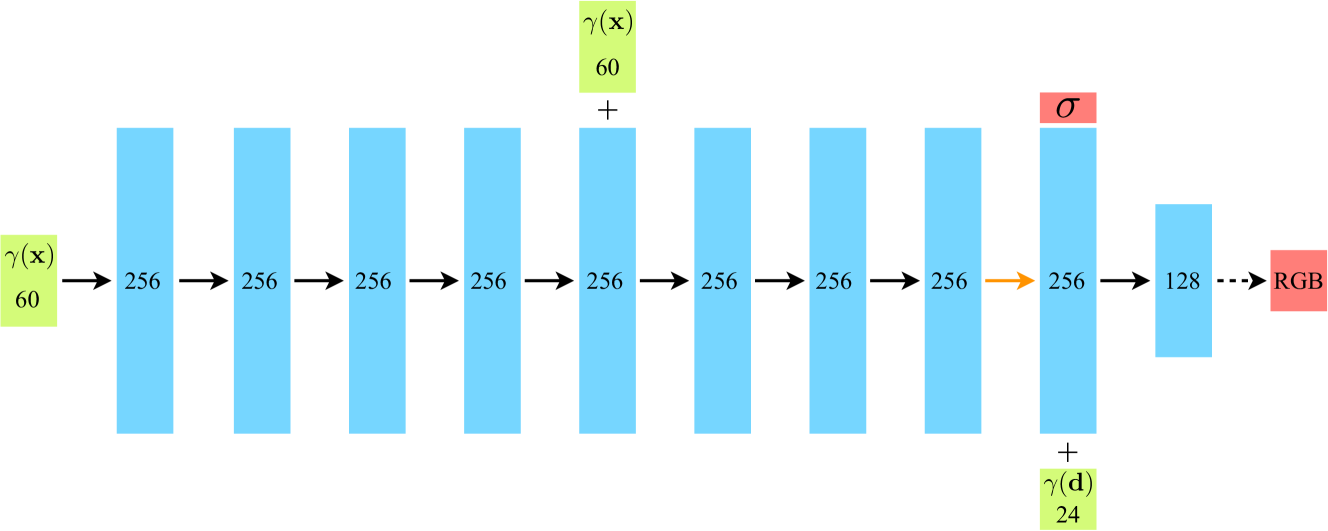
アーキテクチャ

これがMLPのアーキテクチャになります。

具体的には以下の通りです:

• 入力: 5次元の位置と視線方向(x, y, z, θ, φ)

• 位置xは8層の全結合層を通過し, ボリューム密度σを出力

• 位置xからの256次元フィーチャも出力

• このフィーチャと視線方向dを結合し、1層の全結合層を通過

• 最終層がview依存のRGB色を出力

• 全ての層がReLUを活性化関数として使用

つまり、5D入力からボリューム密度と視点依存の色を出力する、複数の全結合層から構成されるシンプルなMLPアーキテクチャが示されています。

個人的重要論文

1. Kajiya, J.T., Herzen, B.P.V.: Ray tracing volume densities. Computer Graphics (SIGGRAPH) (1984)

次は3d gaussian splattingをやりたい....