パターン認識と機械学習 1.1まとめ

パターン認識とは何か？

データの中の規則性を見つけ出し、規則性を使ってデータの異なるカテゴリに分類する

例　手書き文字の数字

数字１つ１つが縦28横28のピクセルの場合、全体として784の実数ベクトルとしてｘを受け取る。この７８４の実数ベクトルを特徴量として規則性を見つける。これを人力で規則性を見つけるのが大変なため機械学習を使用します。

• ベクトル

  向きと大きさを持つ量のこと

• ピクセル

  パソコンの画面や、デジタル写真は、小さな四角形の集まりで構成されています。この一つ一つの四角のこと

• 特徴量

  機械学習において予測の手がかりとなる数値

機械学習

画像１枚１枚をxと置きます。

機械学習では訓練集合とテスト集合、目標ベクトルが存在します。

• xに対応しているこのように分類したいという対象tのことを目標ベクトル
• 機械学習のモデルに訓練させるｘの集合を 訓練集合
• 識別できているか検査するｘの集合をテスト集合

訓練集合を使用して機械学習モデルのパラメーターを目標ベクトルに合うよう調整しテスト集合で目標ベクトルにあっているか確認する。
これが機械学習の手順です。
しかし、入力ベクトルの多様性が大きいので訓練集合は識別できるがテスト集合では識別できないということが起きます。これを過学習といいます。

実際の学習手順

実際の場合には問題を解きやすくするために入力変数を変換します。これを前処理、特徴量抽出と呼びます。

教師あり学習

訓練集合に目標ベクトルがある学習を教師あり学習と呼びその中に

• クラス分類(目標ベクトルが有限個の離散的カテゴリである場合)
• 回帰分類(目標ベクトルが連続変数である場合)
  に分かれます。

教師なし学習

訓練集合に目標ベクトルがある学習を教師あり学習と呼びます。

• 視覚化
• 密度推定
  という２つがありデータの分布などを見るのに使われます。

そしてパターン認識のゴールはパターン認識のゴールは，観測されたデータをもとに，今後観測されるであろうデータを予測することです．

多項式曲線フィッティング

単純な回帰問題をやってみます。

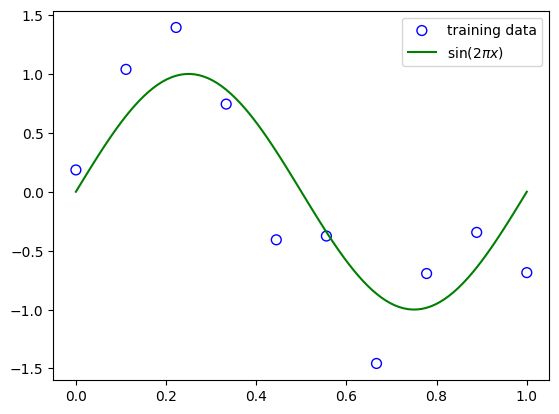
このようなデータがあります。これはsinxの数値にノイズとしてがガウス分布の値をいれてプロットしました。
実際のデータにはこのようなノイズがあり、不正確なものとなります。
目標としては新たな入力があったときに値を予測することです。
この図ではf(x)=sin(x)が大方予測できていると考えられます．

このようなフィッテングを行い次の値を予測することができれば理想です。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
t = np.arange(-5, 5, 0.1)
noise = np.random.normal(loc=0, scale=0.5, size=len(x))
y = np.sin(t)+noise
fig, ax = plt.subplots()
c1,c2,c3,c4 = "blue","green","red","black"      # 各プロットの色
l1,l2,l3,l4 = "sin+noise","sin","abs(sin)","sin**2"   # 各ラベル

ax.set_xlabel('t')  # x軸ラベル
ax.set_ylabel('y')  # y軸ラベル
# ax.set_aspect('equal') # スケールを揃える
ax.grid()            # 罫線
#ax.set_xlim([-10, 10]) # x方向の描画範囲を指定
#ax.set_ylim([0, 1])    # y方向の描画範囲を指定
ax.scatter(t,y, color=c1, label=l1)
ax.plot(t, np.sin(t), color=c2, label=l2)
ax.legend(loc=0)    # 凡例
fig.tight_layout()  # レイアウトの設定
# plt.savefig('hoge.png') # 画像の保存
plt.show()

これらをデータだけで線形であるような関数を用いて予測を行うモデルを線形モデルといいます。

理論

このような数式の訓練データがあるとします。

y(x,W) = w_0 + w_1x + w_2x^2 + w_3x^3 + ...+ w_Mx^M = \sum_{j=0}^{M} w_jx^j

このような訓練データに多項式を当てはめることで係数の値を求める。
Wを任意に固定し誤差関数を使用し最小のものをWの値にする。
二乗誤差の最小化

E(W) = \frac{1}{2}\sum_{n=1}^{N} (y(x_n,W)-t_n)^2

y(x_n,W)が観測値、t_n線形モデルからの予測数値
次数Mを選ぶ問題は残っているが最小の値を出せればWをだすことができます。
この章では具体的な式の展開は省かれています。
具体的なコードはこちらから

このようなデータがある場合最小二乗法を使用し線形モデルにフィッティングを行うとこのようになります。
o次関数でフィッティング（つまり定数)
1次関数でフィッティング（つまり線形回帰）
3次関数でフィッティング
9次関数でフィッティング

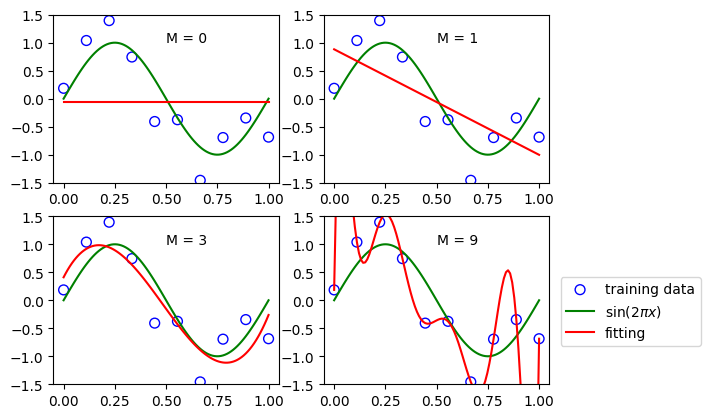
このようになります。9次関数でフィッティングではデータに適合しすぎて過学習が起きているのがわかります。
3次関数でフィッティングが一番いい線形モデルになっていることがわかります。
ここで新たなデータに対しても対応しているかテスト集合を用いて使用します。
ここでは汎化性能を図るために評価する式があります。
平均二乗誤差

E_{RMS} = \sqrt{\frac{2E(W^*)}{N}}

を使用して評価をすると

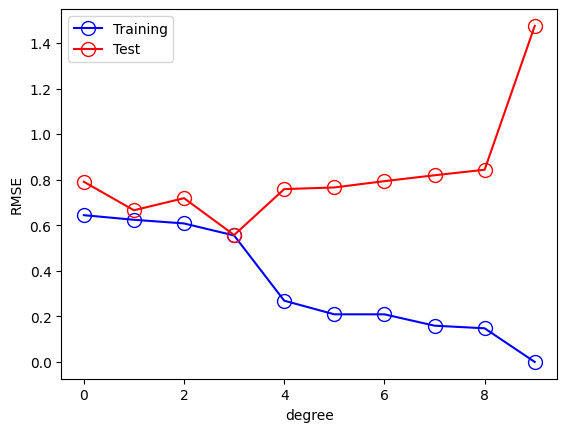
このようにMの数が増えることで過学習が進み３ぐらいがちょうどいい汎化性能があることがわかります。

次にNの値を上げてみましょう。
N = 100に設定します。

10次関数でフィッティング
25次関数でフィッティング
50次関数でフィッティング
100次関数でフィッティング

テスト評価はこのようになります。

70次関数がcちょうどよく汎化しているかなと分かります。
ただこのくらいおおくなるとよくわからなくなりますね..

過学習を防ぐには

正則化を使用することでフィッティングしすぎるのを防ぐ役割をもっています。

E(W) = \frac{1}{2}\sum_{n=1}^{N} (y(x_n,W)-t_n)^2 + \frac{1}{2}||W||^2\\
||W||^2 \equiv W^TW = \sum_{n=0}^{M}w_n^2