はじめに
最近アルゴリズムの勉強をし始めました。
数独を解くプログラムを作る傍ら、せっかくなので自分用にQiita記事にまとめておきます。
今回はクールなアルゴリズムは使いません。
愚直に全探索で解くものを作ります、つまり初心者向けです。
この記事はあれやこれやと賢いやり方が浮かぶ人向けではないためご了承ください
数独の問題の表現
今回使う数独のテーブルはこちら
滅茶苦茶難易度低いやつです、既存のものをExcelでポチポチ作りました。
正常に動作さえすればよいので、難しい必要はないです(人間がチェックするのも大変になるし)
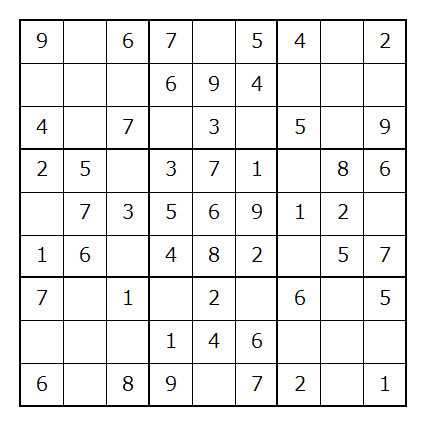
さて、数独問題をどうPython上で表現するかですが、今回はこれに2次元配列を利用することにしました。
マスの中の値をすべて数字で扱いたいため、今回は空欄を0で表現しています。
空欄位置の取得は2重ループで回してenumerate関数によって新たなiterableとなった要素から、要素番号を取得します。
この記述方法最近知ったんですけど、前もってカウンタ用意してカウントアップしたり、継続条件をlen()で指定して要素番号取るより見た目がシンプルで結構好きなんですよね。
# 数独問題を表す2次元配列を定義(空欄を0に設定)
TABLE = [[9, 0, 6, 7, 0, 5, 4, 0, 2],
[0, 0, 0, 6, 9, 4, 0, 0, 0],
[4, 0, 7, 0, 3, 0, 5, 0, 9],
[2, 5, 0, 3, 7, 1, 0, 8, 6],
[0, 7, 3, 5, 6, 9, 1, 2, 0],
[1, 6, 0, 4, 8, 2, 0, 5, 7],
[7, 0, 1, 0, 2, 0, 6, 0, 5],
[0, 0, 0, 1, 4, 6, 0, 0, 0],
[6, 0, 8, 9, 0, 7, 2, 0, 1]]
# 空欄をチェック
for i, items in enumerate(TABLE):
for j, item in enumerate(items):
if item == 0:
print("TABLEテーブルの要素番号[" + str(i) + "][" + str(j) + "]に空欄あり")
TABLEテーブルの要素番号[0][1]に空欄あり
TABLEテーブルの要素番号[0][4]に空欄あり
TABLEテーブルの要素番号[0][7]に空欄あり
.
.
.
TABLEテーブルの要素番号[8][7]に空欄あり
配列要素番号なので、数独はマス目が9x9個あるけど、0~8形式になっているところだけ注意。
これで一応数独問題のテーブルと空欄場所の検出はできるようになった。
空欄に入る数字のチェック
数独は、行、列、3x3で区切られた領域、の3つすべてに、1~9の数字が1つずつ入っている状態を満たす必要があります。
そのため、1つの空欄に対して、3つの条件をすべて満たす数値を小さい順から入れていく方法で進めていこうと思います。
特定の行で使われている数字の列挙
まず手始めに指定された行に対して既に使用されている数字を列挙してset型データとして変数に格納してみます。
# 数独問題を表す2次元配列を定義(空欄を0に設定)
TABLE = [[9, 0, 6, 7, 0, 5, 4, 0, 2],
[0, 0, 0, 6, 9, 4, 0, 0, 0],
[4, 0, 7, 0, 3, 0, 5, 0, 9],
[2, 5, 0, 3, 7, 1, 0, 8, 6],
[0, 7, 3, 5, 6, 9, 1, 2, 0],
[1, 6, 0, 4, 8, 2, 0, 5, 7],
[7, 0, 1, 0, 2, 0, 6, 0, 5],
[0, 0, 0, 1, 4, 6, 0, 0, 0],
[6, 0, 8, 9, 0, 7, 2, 0, 1]]
# m行で既に使用されている数字のsetを表示
def check_row(m):
r_set = set()
# 行に対してのチェック
for cell in TABLE[m]:
if cell != 0:
r_set.add(cell)
print(r_set)
# 4+1 行目で使用されている数字を取得
check_row(4)
{1, 2, 3, 5, 6, 7, 9}
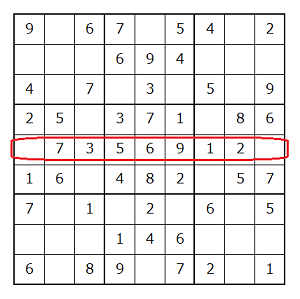
5行目を示すTABLE[4]には[0, 7, 3, 5, 6, 9, 1, 2, 0]が格納されています。
使用されている数字が正しく取得できました。
特定の列で使われている数字の列挙
続いては指定された列に対して同じように使用されている数字を返す関数を作ります。
# TABLE記述省略
# m行で既に使用されている数字のsetを表示
def check_column(n):
c_set = set()
# 列に対してのチェック
for row in TABLE:
if row[n] != 0:
c_set.add(row[n])
print(c_set)
# 7+1 列目で使用されている数字を取得
check_column(7)
{8, 2, 5}
特定の列に対する行のカウントアップは先ほどに比べてほんの少しだけ複雑になります。
foreachによってTABLEから取得した要素の一つ(つまり一行分のデータ)をrowにいったん格納して、さらにrow[n]という形で欲しい行数に格納されているデータを取得しています。
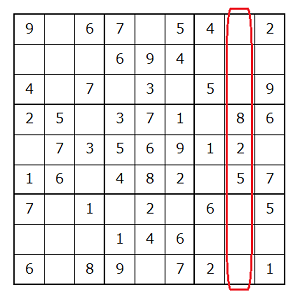
実行結果と照らし合わせてみると、8行目で使われている数字は8,2,5であることから、結果が正しいことが分かります。
m行n列が属する3x3のエリアで使われている数字の列挙
これの実装に若干悩みました。
自分は頭の中で処理の流れを想像して構築することが苦手なため、泥臭く思考を書き出して整理します。

最初は指定されたマス目が属するエリアを考えて、そのエリアごとに使われている数字を返す関数を作ろうかと考えたのですが、普通に考えて商を使えば簡単にできることに気が付いた。![]()
たとえば(4, 7)に該当するマス目が属するエリアは
行 -> 3 * (4 // 3) ~ 3 * (4 // 3) + 2
列 -> 3 * (7 // 3) ~ 3 * (7 // 3) + 2
の間となることがわかります。(ちなみに4//3は、4/3の商部分、つまり1)
これを利用して二重ループでマス目の中の値を取得します。
コードに起こした結果がこちら
# TABLE記述省略
# 指定されたマス目が属するエリアで使用されている数字のsetを表示
def check_area(m, n):
area_set = set()
for a in range(3 * (m // 3), 3 * (m // 3) + 3):
for b in range(3 * (n // 3), 3 * (n // 3) + 3):
print(str(a) + ", " + str(b))
if TABLE[a][b] != 0:
area_set.add(TABLE[a][b])
print(area_set)
# 5行8列目が属するエリアで使用されている数字を取得
check_area(4, 7)
3, 6
3, 7
3, 8
4, 6
4, 7
4, 8
5, 6
5, 7
5, 8
{1, 2, 5, 6, 7, 8}
結果として選択されたマス目が属するエリアにあるすべてのマス目を(行, 列)形式で列挙した後、今までと同じように使用されている数字を表示しています。
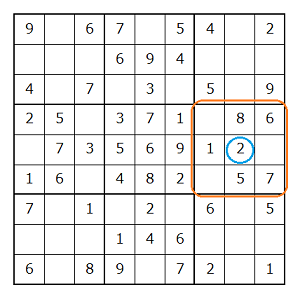
今回(4, 7)と指定したマス目が青丸部分、そして属するエリアがオレンジで囲われた部分です。
エリアで使われている数字が8,6,1,2,5,7であることから、実行結果は正しいことが分かります。
3つのチェックを1つの関数にまとめる
行、列、エリアに対する使用されている数字のチェック処理を、一つの関数にまとめます。
# TABLE記述省略
# m行n列目のセルが属する行、列、エリアで使用されている数字を表示
def check_cell(m, n):
global TABLE
n_set1, n_set2, n_set3 = set(), set(), set()
# 行に対してのチェック
for cell in TABLE[m]:
if cell != 0:
n_set1.add(cell)
# 列に対してのチェック
for row in TABLE:
if row[n] != 0:
n_set2.add(row[n])
# エリアに対してのチェック
for a in range(3 * (m // 3), 3 * (m // 3) + 3):
for b in range(3 * (n // 3), 3 * (n // 3) + 3):
if TABLE[a][b] != 0:
n_set3.add(TABLE[a][b])
print(n_set1)
print(n_set2)
print(n_set3)
# 5行8列目を指定
check_cell(4, 7)
{1, 2, 3, 5, 6, 7, 9}
{8, 2, 5}
{1, 2, 5, 6, 7, 8}
このようになりました。
上から該当する行、列、エリアで使われている数字を列挙しています。
# TABLE記述省略
# m行n列のセルに数値kを入れたとき、そのkが条件を満たすか判定する関数
def check_cell(m, n):
global TABLE
n_set1, n_set2, n_set3 = set(), set(), set()
# 行に対してのチェック
for cell in TABLE[m]:
if cell != 0:
n_set1.add(cell)
# 列に対してのチェック
for row in TABLE:
if row[n] != 0:
n_set2.add(row[n])
# エリアに対してのチェック
for a in range(3 * (m // 3), 3 * (m // 3) + 3):
for b in range(3 * (n // 3), 3 * (n // 3) + 3):
if TABLE[a][b] != 0:
n_set3.add(TABLE[a][b])
# これら3つのsetの和集合を取る
n_union = n_set1.union(n_set2, n_set3)
# 差集合をとり、まだ使われていない数字を取得
n_not_used = {1, 2, 3, 4, 5, 6, 7, 8, 9}.difference(n_union)
print(str(m+1) + " 行目で使われている数字 :" + str(n_set1))
print(str(n+1) + " 列目で使われている数字 :" + str(n_set2))
print("属するエリアで使われている数字 :" + str(n_set3))
print("(" + str(m) + ", " + str(n) + ")に入りうる数字 :" + str(n_not_used))
# 5行9列目を指定
check_cell(4, 8)
5 行目で使われている数字 :{1, 2, 3, 5, 6, 7, 9}
5 列目で使われている数字 :{1, 2, 5, 6, 7, 9}
属するエリアで使われている数字 :{1, 2, 5, 6, 7, 8}
(4, 8)に入りうる数字 :{4}
set型であることを利用して、和集合と差集合の演算を行い最終的に指定したマス目に入れることができる数値を表示しています。
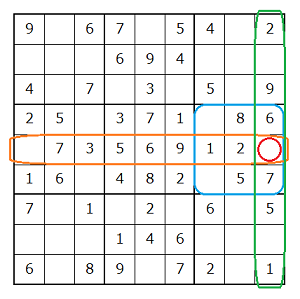
今回は赤丸部分を指定した結果、オレンジ、緑、水色で囲まれているエリアで使われている数字の和集合を取り、さらに1~9の数字との差集合を計算しました。
結果的に赤丸部分に記入可能な数字は4のみという結果が出ましたが、この結果は正しいことが分かります。
さらに検証
1行目の空欄3つについて調べてみました。
check_cell(0, 1)
check_cell(0, 4)
check_cell(0, 7)
(0, 1)に入りうる数字 :{8, 1, 3}
(0, 4)に入りうる数字 :{1}
(0, 7)に入りうる数字 :{1, 3}
数独のテーブルを見ると、この結果もしっかりと正しいことが分かります。
正直要素が少ない順から埋めたら簡単ですが、ここはあえて我慢..
(入りうる数字の候補が少ない順に埋めていく処理は次回以降の予定です)
真偽値で返す関数にする
先ほどの関数のコンソール表示処理部分を消して、戻り値を設定します。
k in n_not_used
この in は、k が n_not_used(使用可能な数字の集合)に属しているかどうかを判定します。
つまり、k が使用可能な数字ならTrue、既に使用されている数字ならFalseを返します。
# TABLE記述省略
# m行n列のセルに数値kを入れたとき、そのkが条件を満たすか判定する関数
def check_cell(m, n, k):
global TABLE
n_set1, n_set2, n_set3 = set(), set(), set()
# 行に対してのチェック
for cell in TABLE[m]:
if cell != 0:
n_set1.add(cell)
# 列に対してのチェック
for row in TABLE:
if row[n] != 0:
n_set2.add(row[n])
# エリアに対してのチェック
for a in range(3 * (m // 3), 3 * (m // 3) + 3):
for b in range(3 * (n // 3), 3 * (n // 3) + 3):
if TABLE[a][b] != 0:
n_set3.add(TABLE[a][b])
# これら3つのsetの和集合を取る
n_union = n_set1.union(n_set2, n_set3)
# 差集合をとり、まだ使われていない数字を取得
n_not_used = {1, 2, 3, 4, 5, 6, 7, 8, 9}.difference(n_union)
# kが選択可能な数値かどうかを真偽値で返す
return k in n_not_used
print(check_cell(0, 1, 4))
print(check_cell(0, 4, 1))
print(check_cell(0, 7, 5))
False
True
False
これで指定した行、列に該当する空欄に入る数字を判定できる関数が完成しました。
実際に数独を解く関数を作成
というわけで冒頭で作った、空欄位置を取得する処理と、先ほど作った特定の空欄に入る数値をチェックする関数を組み合わせてみます。
ただこのままではループ中に組み込む処理として少し使いづらいので、空欄位置を取得する処理を、一番左上の(要素番号が一番若い)空欄を取得する関数として定義します。
# 一番左上の空欄を取得する関数
def find_next_blank(t):
for i, items in enumerate(t):
for j, item in enumerate(items):
if item == 0:
# 順にマス目を調べ、0が初めてあった座標を返す
return i, j
# 81マスの中に一度も0がなければ(-1, -1)を返す
return -1, -1
# 最初の空欄マスを取得
print(find_next_blank(TABLE))
(0, 1)
find_next_blank()関数は、空欄であるマス目の行番号と列番号をtuple型で返します。
数独TABLEの空欄が全て埋まった場合は、(-1, -1)を返すように設定します。
これによってもしfind_next_blank()関数からの戻り値として-1が取得できた場合、正しいか正しくないかは確定ではありませんが、空欄はすべて埋まったため、その段階で処理を終了することができます。
そしていよいよ、check_cell()関数と、find_next_blank()関数を組み合わせて数独を解く関数を作っていこうと思います。
空欄に条件を満たす数値を格納する関数を作る
今回は、先程から使用しているTABLEと、既に完成済みである空欄のない数独を想定して
リスト内包表記で定義したTABLE_COMPを使います。
# TABLE記述省略
# 空欄のない9x9マステーブル(完成後処理確認用)
TABLE_COMP = [[1 for _ in range(1, 10)] for _ in range(1, 10)]
# 一番左上の空欄を検出し、条件を満たす数値を格納する関数
def do(t):
r, c = find_next_blank(t)
# rに-1が格納されていれば、数独完成済み
if r == -1:
print("完成済みです。")
else:
for num in range(1, 10):
# 条件を満たしていればnumを格納
if check_cell(t, r, c, num):
t[r][c] = num
print(str(r) + "行目," + str(c) + "列目に " + str(num) + " を格納")
break
# 空欄のあるテーブルで実行
print(TABLE[0])
do(TABLE)
print(TABLE[0])
まずはTABLEに対して関数を呼び出してみます。
尚、1行目だけ表示しています。
[9, 0, 6, 7, 0, 5, 4, 0, 2]
0行目,1列目に 1 を格納
[9, 1, 6, 7, 0, 5, 4, 0, 2]
空欄があるマス目を自動的に取得して、条件を満たす数値を入力しています。
次に、TABLE_COMPでやってみます。
# 空欄のないテーブルで実行
print(TABLE_COMP[0])
doit(TABLE_COMP)
print(TABLE_COMP[0])
[1, 1, 1, 1, 1, 1, 1, 1, 1]
完成済みです。
[1, 1, 1, 1, 1, 1, 1, 1, 1]
空欄がないTABLE_COMPは、find_next_blank()関数からの戻り値として(-1, -1)が返されているため。
完成済みのデータであることが表示されています。
再帰処理で繰り返し関数を呼び出す
要素番号が一番若い空欄位置を取得し、そこに条件を満たす数値を入れる。
という一連の流れを関数化した上で、その処理の中にさらにその関数自身を呼び出す処理を組み込めば、再帰関数として繰り返し定義した処理を行うことができます。
再帰関数について
まずは確認のため、かんたんな例から。
def rec_func(x):
if x <= 0:
return x
return rec_func(x-1) + x
print(rec_func(10)) # 55
このrec_func()関数は、引数にxを受け取り呼び出された時、まずxが0以下かどうか判定します。
もしxが0以下であれば、戻り値にx自体を返します。
そうでなければ、x-1を引数に指定したrec_func()関数自身の戻り値と、xの和を返します。
再帰関数の処理の流れは少し分かりづらいですが、ビジュアル化すると理解しやすくなります。
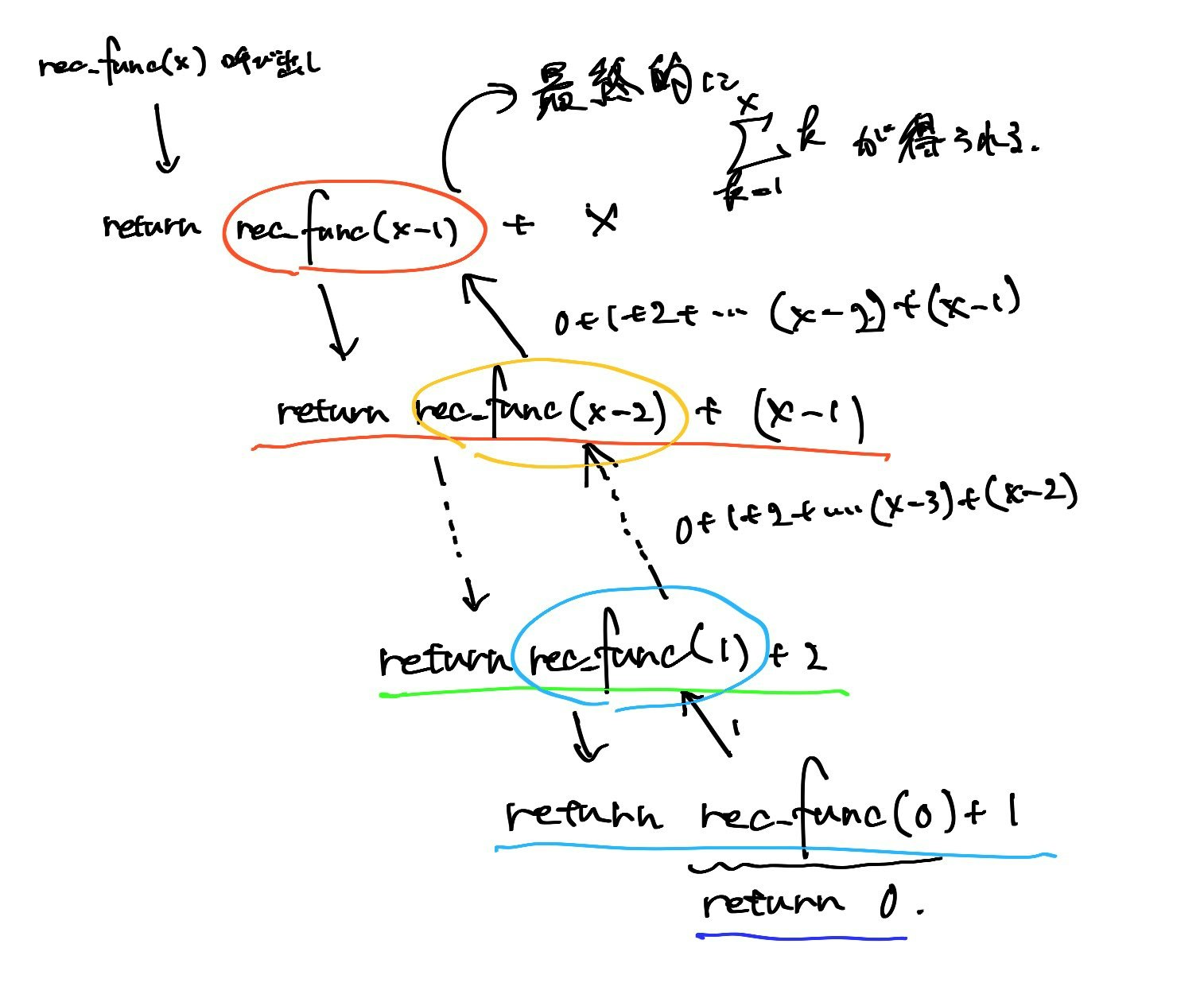
rec_func(x)のreturn文が、rec_func(x-1) + xという形で渡されています。
つまり、rec_func(x)の処理途中でrec_func(x-1)が呼び出され、さらにその関数呼び出し処理の途中で、rec_func(x-2)が呼び出され....という具合に連鎖的に関数内で同じ関数が呼び出されます。
最終的に引数に相当する値が0まで減ると、if x <= 0:を満たしx自体を返します。
この段階からようやく一つ前に呼び出されたrec_func(1)の戻り値である
rec_func(0)+1が0+1という形で判明し、さらにrec_func(2)の戻り値であるrec_func(1)+2が0+1+2となり、この操作を繰り返して、最終的に最初の呼び出し元であるrec_func(x)の戻り値rec_func(x-1)+xに戻ってきます。
この時、戻り値は1からxまでの総和となり、この関数の処理が終わります。
実行結果では、今回rec_func(10)を呼び出しているので、1から10までの総和である55が戻り値として取得され表示しています。
再帰関数化
先程の考え方を利用して、数独を解く関数も再帰関数化します。
# 数独を解く関数
def do(t):
r, c = find_next_blank(t)
# rに-1が格納されていれば、数独完成済み
if r == -1:
return True
# 1 ~ 9の数字を順番にcheck_cell()関数で判定
for num in range(1, 10):
# 条件を満たしていればnumを格納
if check_cell(t, r, c, num):
t[r][c] = num
# do()関数自身を呼び出し条件分岐
if do(t):
return True
t[r][c] = 0
# 1 ~ 9まで一つも条件を満たさなければ戻るためFalseを返す
return False
再帰処理の終了ラインは、空欄がすべてなくなった段階です。
つまり、find_next_blank()関数の戻り値から(-1, -1)を取得できた段階でこの関数の処理を終了できるような構造にします。
先程
if r == -1:
print("完成済みです。")
このような処理を関数に組み込んでいましたが、このコンソール表示部分をTrueを返す処理に変えます。
もしfind_next_blank()関数から有効な座標を取得した場合は、そのマス目に対してfor文で1から9まで順番に条件を満たしているかチェックしながら格納を試みます。
t[r][c] = num の後
この関数自身を呼び出した戻り値から条件判定し、TrueとなったときにこのブロックでもTrueを返すように設定します。
もし違う場合は、マス目に対して再度空欄を意味する0を設定し直し、1~9までいずれも条件を満たさなかった場合にFalseを返します。
完成
from stopwatch import measure_time
# 数独問題を表す2次元配列を定義(空欄を0に設定)
TABLE = [[9, 0, 6, 7, 0, 5, 4, 0, 2],
[0, 0, 0, 6, 9, 4, 0, 0, 0],
[4, 0, 7, 0, 3, 0, 5, 0, 9],
[2, 5, 0, 3, 7, 1, 0, 8, 6],
[0, 7, 3, 5, 6, 9, 1, 2, 0],
[1, 6, 0, 4, 8, 2, 0, 5, 7],
[7, 0, 1, 0, 2, 0, 6, 0, 5],
[0, 0, 0, 1, 4, 6, 0, 0, 0],
[6, 0, 8, 9, 0, 7, 2, 0, 1]]
# m行n列のセルに数値kを入れたとき、そのkが条件を満たすか判定する関数
def check_cell(t, m, n, k):
n_set1, n_set2, n_set3 = set(), set(), set()
# 行に対してのチェック
for cell in t[m]:
if cell != 0:
n_set1.add(cell)
# 列に対してのチェック
for r in t:
if r[n] != 0:
n_set2.add(r[n])
# エリアに対してのチェック
for a in range(3 * (m // 3), 3 * (m // 3) + 3):
for b in range(3 * (n // 3), 3 * (n // 3) + 3):
if t[a][b] != 0:
n_set3.add(t[a][b])
# これら3つのsetの和集合を取る
n_union = n_set1.union(n_set2, n_set3)
# 差集合をとり、まだ使われていない数字を取得
n_not_used = {1, 2, 3, 4, 5, 6, 7, 8, 9}.difference(n_union)
# kが選択可能な数値かどうかを真偽値で返す
return k in n_not_used
# 一番左上の空欄を取得する関数
def find_next_blank(t):
for i, items in enumerate(t):
for j, item in enumerate(items):
if item == 0:
# 順にマス目を調べ、0が初めてあった座標を返す
return i, j
# 81マスの中に一度も0がなければ(-1, -1)を返す
return -1, -1
# 数独を解く関数
def do(t):
r, c = find_next_blank(t)
# rに-1が格納されていれば、数独完成済み
if r == -1:
return True
# 1 ~ 9の数字を順番にcheck_cell()関数で判定
for num in range(1, 10):
# 条件を満たしていればnumを格納
if check_cell(t, r, c, num):
t[r][c] = num
# do()関数自身を呼び出し
if do(t):
return True
t[r][c] = 0
# 1 ~ 9まで一つも条件を満たさなければ戻るためFalseを返す
return False
# 完成したTABLEが実際に正しいかどうかを判定する関数
def check_table(t):
status = True
for r in range(9):
for c in range(9):
# この関数は第4引数の数値が使われていない数字かどうかを判定するため
# 一度でもTrue -> 完成済みTABLEのどこかに重複が発生している
if check_cell(t, r, c, t[r][c]):
status = False
return status
# 数独テーブルを表示する関数
def display_table(t):
for _ in t:
print(_)
# 実行部分
# 未完成状態の数独の表示
display_table(TABLE)
# 数独を解く
print("↓")
print("処理時間 : " + measure_time(do, TABLE))
# 完成後の数独の表示
display_table(TABLE)
# check_table()関数で完成後の数独が適切な常態かチェック
w = "この解答は正しいです。" if check_table(TABLE) else "この解答は正しくありません"
print(w)
というわけで数独を解くプログラムが完成しました。
今回はさらに、実際に解かれたものが本当に正しいかどうかを判定する関数と、数独表示用の関数を追加しました。
# 完成したTABLEが実際に正しいかどうかを判定する関数
def check_table(t):
status = True
for r in range(9):
for c in range(9):
# この関数は第4引数の数値が使われていない数字かどうかを判定するため
# 一度でもTrue -> 完成済みTABLEのどこかに重複が発生している
if check_cell(t, r, c, t[r][c]):
status = False
return status
# 数独テーブルを表示する関数
def display_table(t):
for _ in t:
print(_)
check_table()関数では、引数に受け取った数独テーブルのすべての行、列に対してcheck_cell()関数を実施し値が正しいかどうかを判定します。
check_cell()関数の構成上、そのマスの縦、横、エリアすべてでまだ使われていない数字を列挙して、その集合に第四引数の数値が含まれているかどうかで判定していますが、適切な値が格納された場合は、その集合には一つも数字が含まれていない空集合になるため、k in n_not_usedはFalseとなります。
ややこしいですが、check_cell()が一度でもTrueだったときにstatusにFalseを格納して返し、そうでない場合はTrueを返します。
これにより、check_tableの戻り値がTrueだった時に、引数に渡したテーブルデータが正しく完成された数独であることを示すことができます。
import time
# 関数の実行時間を返す
def measure_time(func, n):
start = time.perf_counter_ns()
func(n)
end = time.perf_counter_ns()
dt = end - start
if dt >= 1000000000:
# ns -> s
dt = str(dt / 1000000000) + " s"
elif dt >= 1000000:
# ns -> ms
dt = str(dt / 1000000) + " ms"
elif dt >= 1000:
# ns -> μs
dt = str(dt / 1000) + " μs"
else:
dt = str(dt) + " ns"
return dt
また、今回はdo()関数の処理時間を計測するため、同ディレクトリに時間計測用のクラスを作り、そのクラスが持つ関数を使用しています。
[9, 0, 6, 7, 0, 5, 4, 0, 2]
[0, 0, 0, 6, 9, 4, 0, 0, 0]
[4, 0, 7, 0, 3, 0, 5, 0, 9]
[2, 5, 0, 3, 7, 1, 0, 8, 6]
[0, 7, 3, 5, 6, 9, 1, 2, 0]
[1, 6, 0, 4, 8, 2, 0, 5, 7]
[7, 0, 1, 0, 2, 0, 6, 0, 5]
[0, 0, 0, 1, 4, 6, 0, 0, 0]
[6, 0, 8, 9, 0, 7, 2, 0, 1]
↓
処理時間 : 1.4159 ms
[9, 8, 6, 7, 1, 5, 4, 3, 2]
[3, 2, 5, 6, 9, 4, 7, 1, 8]
[4, 1, 7, 2, 3, 8, 5, 6, 9]
[2, 5, 4, 3, 7, 1, 9, 8, 6]
[8, 7, 3, 5, 6, 9, 1, 2, 4]
[1, 6, 9, 4, 8, 2, 3, 5, 7]
[7, 4, 1, 8, 2, 3, 6, 9, 5]
[5, 9, 2, 1, 4, 6, 8, 7, 3]
[6, 3, 8, 9, 5, 7, 2, 4, 1]
この数独は正しいです。
実行結果は1.4159ミリ秒でした。
今回実装した全探索型の関数では、数独の内容によっては実行にかかる時間に天と地の差が出ます。
そこで、次は下のような高難度の数独でやってみます。
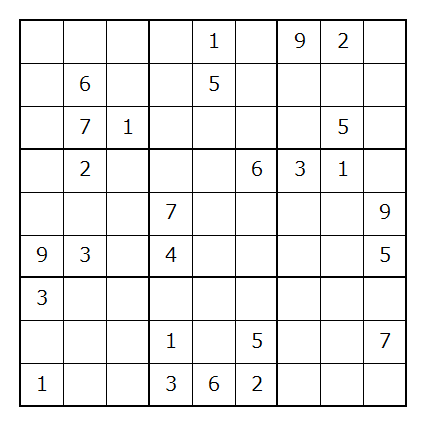
これを2次元配列に落とし込み、TABLE2という変数名で同じく実行してみます。
TABLE2 = [[0, 0, 0, 0, 1, 0, 9, 2, 0],
[0, 6, 0, 0, 5, 0, 0, 0, 0],
[0, 7, 1, 0, 0, 0, 0, 5, 0],
[0, 2, 0, 0, 0, 6, 3, 1, 0],
[0, 0, 0, 7, 0, 0, 0, 0, 9],
[9, 3, 0, 4, 0, 0, 0, 0, 5],
[3, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 5, 0, 0, 7],
[1, 0, 0, 3, 6, 2, 0, 0, 0]]
[0, 0, 0, 0, 1, 0, 9, 2, 0]
[0, 6, 0, 0, 5, 0, 0, 0, 0]
[0, 7, 1, 0, 0, 0, 0, 5, 0]
[0, 2, 0, 0, 0, 6, 3, 1, 0]
[0, 0, 0, 7, 0, 0, 0, 0, 9]
[9, 3, 0, 4, 0, 0, 0, 0, 5]
[3, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 5, 0, 0, 7]
[1, 0, 0, 3, 6, 2, 0, 0, 0]
↓
処理時間 : 424.5753 ms
[5, 4, 3, 8, 1, 7, 9, 2, 6]
[8, 6, 9, 2, 5, 3, 4, 7, 1]
[2, 7, 1, 6, 4, 9, 8, 5, 3]
[7, 2, 4, 5, 9, 6, 3, 1, 8]
[6, 1, 5, 7, 3, 8, 2, 4, 9]
[9, 3, 8, 4, 2, 1, 7, 6, 5]
[3, 5, 6, 9, 7, 4, 1, 8, 2]
[4, 9, 2, 1, 8, 5, 6, 3, 7]
[1, 8, 7, 3, 6, 2, 5, 9, 4]
この数独は正しいです。
結果を見ると、先程の簡単な数独にくらべて299倍も処理に時間がかかりました。
単純な全探索はかなりロスが多いため、プログラムの見直しが必要です。
次回以降は、処理を効率化し、実行にかかる時間を減らしていくことを目標とします。
次↓