Typical DP Contest (Atcoder) のA問題をプログラム初心者が考えてみた part1 bit全探索 #Python

はじめに

自分はPythonを勉強し始めたばかりの初学者であるが、Qiitaで頻繁に見かけるAtCoder（所謂競技プログラミングってやつ？）というやつが気になった。

ただ自分は本当にまだプログラミングの世界に触れたばかりなので、ぶっちゃけプログラミングで競技する程の実力など無いし、さほど競う事に興味は持っていない。
ただ、其処で出題されていたA問題を見て、その問題自体はとても興味深く、どのようにプログラムとして解くか悩んだため、初学者なりに 自分で考えてみることにした。

また、この記事が自分と同じようなプログラム初学者達にとって、少しでも参考になればと思う。

ちなみにA問題 ↓

出題内容

Problem Statement
$N$ 問の問題があるコンテストがあり、
$i$ 問目の問題の配点は $p_i$点である。
コンテスタントは、この問題の中から何問か解き、解いた問題の配点の合計が得点となる。このコンテストの得点は何通り考えられるか。

Constraints
1≤N≤100
1≤p_i≤100

Input Format
入力は以下の形式で標準入力から与えられる。

$N$
$p_1 p_2 ... p_N$

Output Format
答えを一行に出力せよ。

Sample Input 1
3
2 3 5
Sample Output 1
7
(0, 2, 3, 5, 7, 8, 10 の 7 通りの得点が考えられる。)

Sample Input 2
10
1 1 1 1 1 1 1 1 1 1
Sample Output 2
11
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 の 11 通りの得点が考えられる。)

このような問題であり、つまり配点が1～100点の問題が全部で1～100問あって、それを解いたときに取りうる合計点のパターンは何通りあるのかという問題っぽい。

数学(高校・大学入試レベル程度)は個人的に好きだが、こういった問題は初めてだったため、問題文を見ただけで眩暈がした。

考えたこと

とりあえず簡単な例を...

まず、問題文から簡素な例を挙げて考えてみた。
例えば問題が全部で3問あり、配点がすべて1点のパターン

問題1	問題2	問題3	合計点
×	×	×	0
○	×	×	1
×	○	×	1
○	○	×	2
×	×	○	1
○	×	○	2
×	○	○	2
○	○	○	3

問題1つあたり正解か不正解かの2通りあり、問題はそれぞれ区別される。
問題数が増えるごとにそのパターンが問題数分冪乗されていき、3問の場合は $2^3=8$ 通りとなる。
つまり、問題数が$N$問であるならば、考えられるパターンは $2^N$ 通りになる。

これら問題ひとつひとつが正解かどうかを判断し、正解ならばその問題に紐づいた配点を合計点に加算し、不正解ならば無視して次の問題の判定に移行する。というようなプログラムを作る必要がありそうだ。

正解か不正解かの判別方法

そこで重要になるのが、$i$ 番目の問題が正解かどうかを、どのようにプログラムで扱い表現するかという所であった。
まず直感的に思いついたのがbool型のlistもしくは0か1が格納されたlistを作る事だった。

0と1で表現するほうが簡単そうだったためそちらを選択
先ほどの○×表を2進数表記すると下図のようになる、尚、問題の並びは都合を考えて逆にした。

問題3	問題2	問題1
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

これなら、$i$ 番目の問題が0ならば無視、1ならば配点 $p_i$ を合計点に加点
という形で実現ができそう。

そして、これらの0と1の並びは、それらを2進数表記と見立てて、10進数に直すと
000 = 0
001 = 1
010 = 2
という具合に変換できる。
一番右の列に10進数表記した数値を追加すると下図のようになる。

問題3	問題2	問題1	10進数表記
0	0	0	0
0	0	1	1
0	1	0	2
0	1	1	3
1	0	0	4
1	0	1	5
1	1	0	6
1	1	1	7

10進数表記を見ると、単純に0から始まり1ずつカウントアップしているだけだ。
そのため、これはループ処理でうまいこと出来そうな感じがした。

当初は正解不正解の情報を持つlist型データを作る事を考えていたが、ループ内のカウンタをそのまま2進数変換すればそのまま使えることに気が付いた。
なのでまずは手始めに、正解不正解のパターンを2進数表記で書き出すことにした。

N = 3
for i in range(2**N):
    # カウンタiを2進数表記
    print(format(i, 'b'))

結果

format関数を使い、カウンタiを2進数に変換して表示している。
ただこれだと必要最低限の桁数しか表示されないため、0埋めをして表示した。
0埋めはformat関数の第二引数に、0{桁数}bという形で指定すると実現可能。
format関数内を以下のように変更

print(format(i, '0' + str(N) + 'b'))

結果

これで正解不正解の全パターンを2進数表記で書き出すことが出来が、更に各桁ごとに0か1かを判断する必要がある。
昔C言語を勉強した時に触れた、ビットシフトという手法を思い出し、色々と調べてみた。
ビットシフトに関しては、すでに分かりやすくまとめられた記事があるため割愛。

手始めに、簡易的なビット演算をPythonでやってみようと思った。
以下の例は、10進数表記で13という値を、2進数表記で表示した後、ビットシフトを行い結果を表示している。

num = 13
print("numを10進数表記: " + str(num))
num_b = format(num, '08b')
print("numを2進数表記 : " + num_b)
num_r = num >> 1
print("numを右に1ビットシフト:" + format(num_r, '08b'))
num_r = num >> 3
print("numを右に3ビットシフト:" + format(num_r, '08b'))
num_s = num << 1
print("numを左に1ビットシフト:" + format(num_s, '08b'))
num_s = num << 4
print("numを左に4ビットシフト:" + format(num_s, '08b'))

結果

numを10進数表記: 13
numを2進数表記 : 00001101
numを右に1ビットシフト:00000110
numを右に3ビットシフト:00000001
numを左に1ビットシフト:00011010
numを左に4ビットシフト:11010000

実行結果から、ビット演算記号の後に指定した値分ずれていることがわかる。

これと、もう一つは論理積(AND)を利用する。
論理演算はAND, OR, NOT, NAND, NOR, XORと色々あるが、ここでの説明は割愛する。

ANDに関しても、先ほど掲示した記事に詳しく書かれている。

Pythonでは論理積を&を使って表すことが出来る。
以下はビットシフトと論理積の組み合わせにより、2進数表記された値の1桁目が1か0かを判別するコードである。

N = 6
N_b = format(N, '0' + str(N) + 'b')

# Nの2進数0埋め表記
print(N_b)
# 000110と000001の論理積を取る
# つまり、1桁目が1なら1, 0なら0が返ってくる
print(int(N_b) & 1)

# Nを左に1ビットシフト
N_b = N >> 1
print(format(N_b, '0' + str(N) + 'b'))
print(N_b & 1)

# さらにNを1左シフト
N_b = N_b >> 1
print(format(N_b, '0' + str(N) + 'b'))
print(N_b & 1)

# Nを右に2シフト
N_b = N << 2
print(format(N_b, '0' + str(N) + 'b'))
print(N_b & 1)

結果

これを応用すると、正解か不正解かを示す2進数の値を1桁ずつ判定することが出来る。

下では、例として $N$ を3として、それぞれのパターンでどの桁が1かを判別し表示している。

N = 3
# 全回答パターン(2のN乗個)数分繰り返す
for i in range(2**N):
    print()  # 改行
    print(format(i, '0' + str(N) + 'b'))  # 2進数表記
    # 桁数分繰り返す
    for j in range(N):
        # カウンタiを右にjシフトし、1との論理積を条件判定(1ならTrue)
        if i >> j & 1:
            print(str(j+1) + "桁目が○")

結果

000

001
1桁目が○

010
2桁目が○

011
1桁目が○
2桁目が○

100
3桁目が○

101
1桁目が○
3桁目が○

110
2桁目が○
3桁目が○

111
1桁目が○
2桁目が○
3桁目が○

例として i が5 (101)の時を考える

1週目のループでは j は0である、最初の条件文では i は0桁右にシフトされる(要するにビットシフトされていない)
この時1桁目が1であるかどうかを論理積を使い判定している。
101 & 001 は 001 であるため、Trueとなり"1桁目が○"がコンソールに表示された。
2週目のループでは j は1であり、 i は1桁右にシフトされる
010 & 001 は 000 であるため、Falseとなりifブロック内の処理は実行されなかった。
3週目のループでは j は2であり、 i は2桁右にシフトされる
001 & 001 は 001 であるため、Trueとなり"3桁目が○"がコンソールに表示された。

以上のような手順で、すべての桁に対して0か1かを判定することが可能になった。
これらを利用して、本題に戻りA問題を解いてみる。

コーディング結果

まずは分かりやすいように、コメントやコンソール表示処理をたっぷり入れて作った。

Typical_DP_Contest_A_1.py

N = int(input("数値を入力："))
a = list(map(int, input("整数値を複数入力：").split()))
# 合計値のリスト用に重複データを持たないset型データを用意
total_list = set()

for i in range(2 ** N):
    # 合計点
    total = 0
    for j in range(N):
        if i >> j & 1:
            total += a[j]
    total_list.add(total)
    # 各要素0か1かの全パターンとその時の合計点を網羅
    print(format(i, '0' + str(N) + 'b') + " : " + str(total))

print(total_list)
print("とりうる合計値は全部で " + str(len(total_list)) + " 通り")

結果

>>数値を入力：3
>>整数値を複数入力：2 3 5
000 : 0
001 : 2
010 : 3
011 : 5
100 : 5
101 : 7
110 : 8
111 : 10
{0, 2, 3, 5, 7, 8, 10}
とりうる合計値は全部で 7 通り

入力値10 各配点1点の時も正しい結果が出た
(2の10乗のパターンすべて表示されるためここでは割愛)

各配点は標準入力から半角スペースを区切り文字として複数受け取るが、その時受け取った文字列型のデータを、map関数を使いint型に変換しながら整数のみのリストを作り、変数に格納している。
この

list(map(int, input().split()))

という処理は、競プロでは度々使われるみたい。
自分は input().split() までは知っていたけど、文字列を整数型に変えながらリストに突っ込む一番よさそうな処理が分からずにGoogle先生に聞いた。

合計点数のパターンは重複を必要とせず、最終的には何通りあるか分かれば良いため、set型データを用意しそこに格納した。

右に j ビットシフトを行い1桁目に1がある場合はその問題が正解となるため、問題に対応した配点a[j]が合計点totalに追加される。
この処理を繰り返すと、各解答パターン i に対する合計点が算出できるため、外側のループの最後にtotal_listに合計点を追加する。

最終的にtotal_listには重複する値が排除された状態で、取りうる合計点が格納されているため、その要素数を取得すればA問題で欲しい結果が得られる。

余分な記述を減らすとこんな感じ。

Typical_DP_Contest_A_2.py

N = int(input())
a = list(map(int, input().split()))
total_list = set()

for i in range(2 ** N):
    total = 0
    for j in range(N):
        if i >> j & 1:
            total += a[j]
    total_list.add(total)
print(str(len(total_list)))

結果

>>3
>>2 3 5
7

>>10
>>1 1 1 1 1 1 1 1 1 1
11

>>20
>>1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 4 4 4 8
43

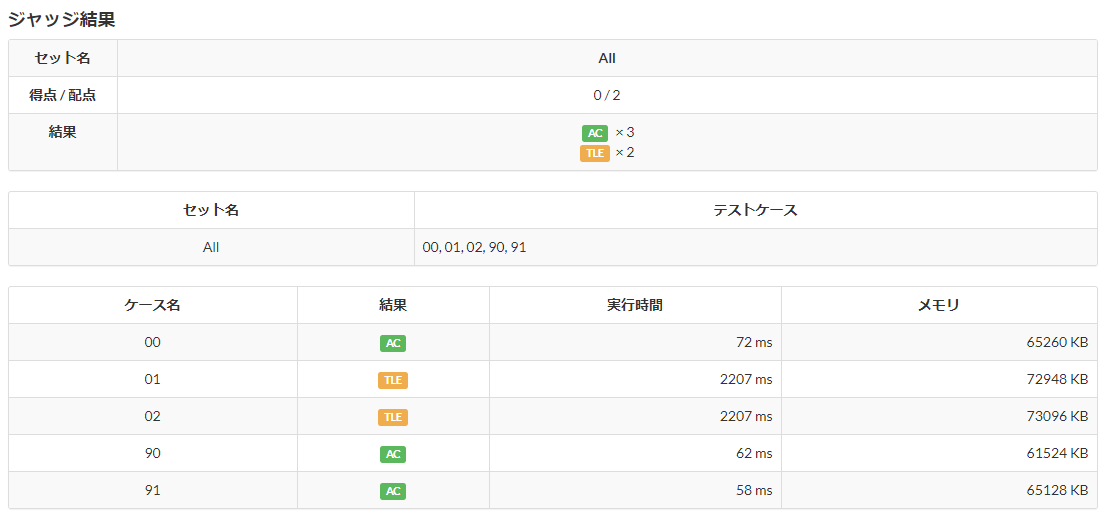
上記のデータを提出してみるとこんな結果が。

ACはAcceptedの意で、つまり正答だよということ。
TLEは指定された実行時間内にプログラムが終わらなかったよということ、つまりこれが一つでもあるならば不合格。

それもそのはずで、今回作成したプログラムは考えられるパターンを全探索する愚直なもので
$2^N$ 通りのパターンをすべて試しているので、当然計算量は $Q(2^N)$ と指数関数的に増える。

要するにこんなんじゃ全然ダメだよってこと。

まとめ

どうやらAtCoderの問題達は工夫して解く必要がありそう。
とりあえずGoogle先生使って色々模範解答的なの探ってみたけど、動的計画法という聞いたことあるようなないようなな単語が出てきた、その内容もプログラムの処理内容は正直現段階ではさっぱり。
ていうかそもそもTypical DP ContestのDPって動的計画法って意味なのねって感じ。

今回の主目的は

プログラム触ってあんまり経ってない自分のような初学者が、AtCoderで出されている問題を、Python使って解答出せるようなプログラム作ろう。
他の初学者の人たちがこの記事に辿り着いたときに、少しでも参考になればいいな

って感じなのでとりあえず達成という事で。

ということもあって、競プロガチ勢の有難い難解アドバイスや、つよそうなエンジニアの重箱の隅をつつくような指摘コメントは正直この記事ではノーサンキューなので、其処らへんはご了承願いたい。

なんだかんだ結構興味沸いたので色々調べて勉強してみるか～

次できました↓↓

問題1	問題2	問題3	合計点
×	×	×	0
○	×	×	1
×	○	×	1
○	○	×	2
×	×	○	1
○	×	○	2
×	○	○	2
○	○	○	3

問題1	問題2	問題3	合計点
×	×	×	0
○	×	×	1
×	○	×	1
○	○	×	2
×	×	○	1
○	×	○	2
×	○	○	2
○	○	○	3

問題1	問題2	問題3	合計点
×	×	×	0
○	×	×	1
×	○	×	1
○	○	×	2
×	×	○	1
○	×	○	2
×	○	○	2
○	○	○	3