前回はこちら↓↓
part2では、 $i$ 問目が解けた時点での合計点の集合 $S_i$ を、 $i$ が $1$ の時から $N$ になるまで下から順に考えていくボトムアップ方式(配るDP)を採用し、プログラムを完成させた。
その結果、part1で作成したbit全探索型のプログラムとは比較にならないほど高速に演算することが出来た。
今回このpart3ではpart2とは逆に、 $i$ が $k$ のとき、 $k-1$ を考える、というような。上から下へトップダウン方式(貰うDP)の考え方で作成していこうと思う。
使用する問題は同じくTypical DP Contest の A問題
↓↓
考え方
以前$i$ 問目を解き終えた時にとりうる合計点の集合 $S_i$ を考えたが
今回は少し考え方を変えようと思う。
$i$ 問目を解き終えた時に合計点 $j$ を取りうるかどうかを、真偽値 $dp[i][j]$ で表現する。
取りうるなら $1$ を、有りえない時は $0$ を格納する。
$dp[i][j]$ を考えるにあたり、一先ず $dp[i-1][j]$ を考えてみる。
$dp[i-1][j]$ の示すものは、 $i-1$ 問目を解き終えた時点で合計点 $j$ を取りうるか、というものであるが
この $dp[i-1][j]$ が $1$ の時、どのように考えられるだろうか。
$i$ 問目は、正解か不正解かの二択なので、考えられる分岐は
- $dp[i][j] = 1 \quad\quad\quad\quad$
- $dp[i][j+p_{i-1}] = 1\quad$
この二つである。
上は、前の問題までの合計点で既に $j$ 点を獲得しているため、不正解の場合は点数加算なしでも $dp[i][j] = 1$ を満たしていることは自明である。
下は、前の問題までの合計点で既に $j$ 点獲得していて、更に $i$ 問目も正解しているため、その時の得点が前回の合計点にプラスされる。
この時、各配点を表す $p_i$ は、コマンドラインから配列で受け取るため、 $i$ 問目の得点が$p_{i-1}$ となる点に注意する。
そうすると、$i$ 問目を解き終えた時点での合計点は$j + p_{i-1}$ 点となるため、 $dp[i][j+p_{i-1}] = 1$ を満たすことになる。
この操作を区間 $0 \leq i \leq N$ で行うことにより、2次元配列 $dp$ が完成し、$dp[N]$ に含まれる $1$ の数を計上することによって、その時点で取りうる合計点のパターンを取得可能である。
また、 $i = 0$ の時は、まだ問題を解いていない状態として考え、その時取得している合計点 $j$ は必ず $0$ であることから
この時の状態を $dp[0][0] = 1$ というように初期条件とする。
以上の考え方をコードにしていく。
コーディング
まず、2次元配列 $dp$ を定義し、どの程度のサイズが必要か考えてみる。
各配点が $p_i$ で与えられる時、考えられる最高得点は、与えられた各配点の合計点となる。
また下限は常に0点であるため、2次元目に必要な要素数は
$1 + \sum_{i=0}^{N-1} p_i$ 個である。
例としてSample Input 1で与えられている条件で実行してみる。
N = 3
p = [2, 3, 5]
# i問目時点で合計点がjになるかどうかのテーブル
dp = [[0 for i in range(sum(p)+1)] for j in range(N+1)]
dp[0][0] = 1
print(*dp, sep="\n")
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
全3問で各配点が2点, 3点, 5点の時に取りうる最高合計点が10点であることから、最低得点の0点と合わせて水平方面に11個の要素がある。
また、問題数が全部で3つなので、1問も解いていない時の状況と合わせて垂直方面に4個の要素がある。
$dp$ テーブルは、図にすると下のように
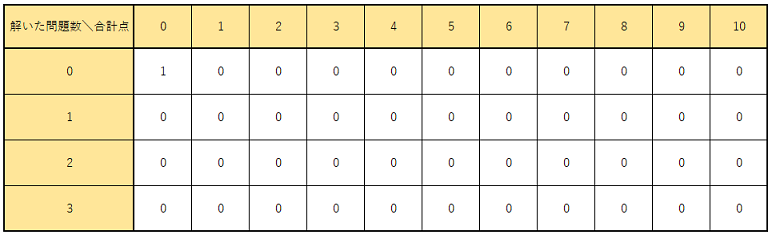
この状態のテーブルが初期条件として与えられ、このテーブルに対して操作を繰り返すことで、最終的に一番下の行の1の数が合計点のパターン数となる。
次に下のような処理を加える。これが具体的にテーブルに対して操作を繰り返す。
# 省略
for i in range(1, N+1):
for j, d in enumerate(dp[i-1]):
if d:
dp[i][j] = 1
dp[i][j+p[i-1]] = 1
print(*dp, sep="\n")
$i = 0$ に関しては、必ず $j$ は$0$のみとなるため、ループ処理は $i = 1$ から $N$ までとした。
内側では、一つ前の行を参照し、列に対してループしている。
つまり、これによって一つ前の問題の解答時点で、合計点が $0$ 点から $sum(p)+1$ 点までの真偽値を取得できる。
ループ過程で取り出した真偽値を $d$、その時の合計点を $j$ として、その $d$ が1である時
つまり$i-1$ 問目解答時点で合計点が $j$ 点であることがあり得るため、この時に以下の処理を行う。
- $dp[i][j]$ に $1$ を代入
- $dp[i][j+p_{i-1}]$ に $1$ を代入
これがif文のブロック内の処理に当たる。
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0]
[1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
実行結果を図にすると以下のようになる。
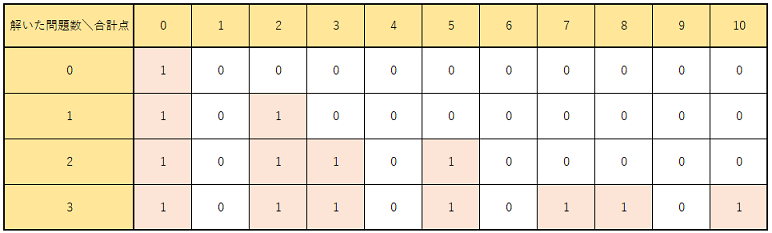
この図、実は前回のpart2で考えるために例に出した図と同じものを指している。
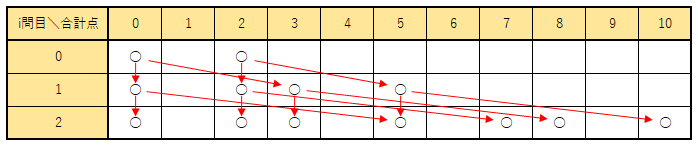
今回実行結果に表示された図の下3行部分がこれにあたる。
最終的に完成したコードはこちら。
N = int(input())
p = list(map(int, input().split()))
# i問目時点で合計点がjになるかどうかのテーブル
dp = [[0 for i in range(sum(p)+1)] for j in range(N+1)]
dp[0][0] = 1
for i in range(1, N+1):
for j, d in enumerate(dp[i-1]):
if d:
dp[i][j] = 1
dp[i][j+p[i-1]] = 1
print(dp[N].count(1))
$dp$ テーブルの $N$ 行目に含まれる $1$ の数をcount()関数を使って算出した。
>>3
>>2 3 5
7
>>10
>>1 1 1 1 1 1 1 1 1 1
11
このコードを提出すると、結果は以下の通りになった。
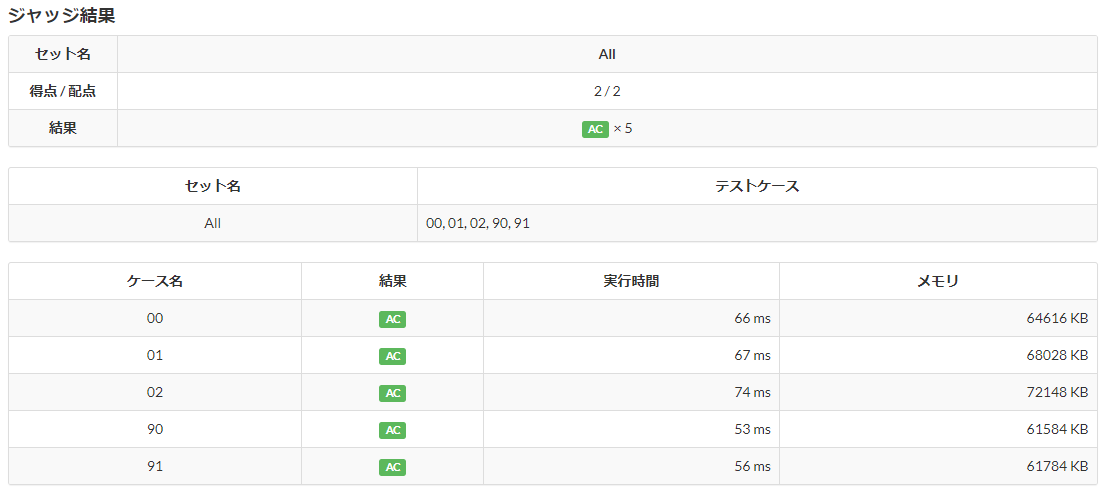
前回作成した処理には若干速度では劣るが、全てのケースでACとなり合格。
計算速度の比較
この記事のシリーズで作成した3つの処理をすべて関数化し、それぞれの速度を比較してみる。
from Sudoku_Project.stopwatch import measure_time1
def exh_search():
total_list = {0}
for i in range(2 ** N):
total = 0
for j in range(N):
if i >> j & 1:
total += p[j]
total_list.add(total)
return len(total_list)
def bu_search():
total_list = {0}
for i in range(N):
for total in list(total_list):
total += p[i]
if total not in total_list:
total_list.add(total)
return len(total_list)
def td_search():
dp = [[0 for i in range(sum(p) + 1)] for j in range(N + 1)]
dp[0][0] = 1
for i in range(1, N + 1):
for j, d in enumerate(dp[i - 1]):
if d:
dp[i][j] = 1
dp[i][j + p[i - 1]] = 1
return dp[N].count(1)
N = int(input())
p = list(map(int, input().split()))
print(measure_time1(exh_search))
print(measure_time1(bu_search))
print(measure_time1(td_search))
>>3
>>2 3 5
10.1 μs
3.5 μs
10.4 μs
>>10
>>1 1 1 1 1 1 1 1 1 1
1.1402 ms
10.1 μs
26.4 μs
>>20
>>1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 3 3 3 4 5
1.4856267 s
22.5 μs
63.6 μs
最速はボトムアップ方式の関数となり、時点でトップダウン方式の関数となりました。