SSR率1%のガチャを100回引いたらどれぐらいの確率で引けるんだろう・・・?
ある人は100%! と言う
このマヌケが!
箱の中の賞品が有限個なら引くたびに当たりの確率は上がり
全て引き切るまで試行すればもちろん100%の確率となるが
ソシャゲのガチャは違う
天井付きのガチャシステムならまだしも、それがないゲームならいくら引いても単発当たりの確率は固定だ
実際に数学的に計算しよう
排出率1%のSSRを引いた時を当たりとするのであれば、単発で当たりを引かない確率は99%だ
今回考えるべき結果は、100回引いて少なくとも1回当たりを引く確率である。
この少なくとも1回以上という条件がなかなか曲者なのだが、中学でちゃんと数学の授業を聞いていた人なら簡単にわかるだろう
このような確率は、余事象を考えるとたやすく算出できる。
少なくとも1回以上当たりを出す確率は、100回引いて1回も当たりを引けない確率の余事象であると考えられる。
単発で当たりを引けない確率が99%なので、それが100回連続して起こる確率は$0.99^{100}$となる
これの余事象を考えればよいので、$1 - 0.99^{100}$ が今回ほしい確率である。
これを計算すると、$0.63396765872...$となり
確率に直すと約63.4%だと言える
さて、今回はSSR排出率1%(1/100)のガチャを100回試行した時にSSRを引ける確率を考えたが、他の数値についても知りたくなった。
一般化してみる
確率1/nの事象をn回試行して、少なくとも1回は事象が起こる確率は、n回連続外れる確率の余事象なので
$$1 - (1 - \frac{1}{n})^n $$
となる
このnをどんどん大きくして、限りなく∞に近づけたときどうなるだろうか?つまり
$$\lim_{n \to \infty}1 - (1 - \frac{1}{n})^n$$
を考えてみる
$\lim_{n \to \infty}(1 - \frac{1}{n})^n$ この部分、見覚えないだろうか
おそらく高校時代理系だったキミなら思い当たる節があるハズ
ネイピア数$e$の定義の形に似ている
$$\lim_{n \to \infty}(1 + \frac{1}{n})^n = e$$
$$ e = 2.718281828459...$$
せっかくならこの式を使いたいので、先ほどの $\lim_{n \to \infty}(1 - \frac{1}{n})^n$ をなんとかして変形する。
$1 - \frac{1}{n} \quad$ を $\quad1 + \frac{1}{(-n)}\quad$ としてみると
$$\lim_{n \to \infty}(1 + \frac{1}{(-n)})^n$$
さらに次数のnを無理やり
$$\lim_{n \to \infty}(1 + \frac{1}{(-n)})^{-(-n)}$$
とすることもできる
$-n = N \quad$とおくと
$$\lim_{n \to \infty}(1 + \frac{1}{N})^{-N}$$
となり、これは結局$\quad\frac{1}{e}\quad$となることがわかる
なので今回求めたい確率は
$$\quad1 - \frac{1}{e} = 0.63212055882...$$
ということで、約63.2%となる
この確率が示すものは一体何か。
ざっくり言うと、限りなく確率が0に近い事象を、果てしなく永遠に試行した時に起こる確率である。
nが増えれば増えるほど、$\frac{1}{n}$の値は小さくなる。
単発でSSRを引く確率がこれにあたるので、nを∞に近づけた時、その確率は0に収束していく。
さらに簡単に言ってしまうと、起こりえないことを無限にやった時、約63.2%の確率で1回は起こるよ。
と言った感じ
nがいくつでもあまり確率は変わらない?
nが100の場合だと約63.4%、nが限りなく大きい場合は約63.2%
となるとこの$\quad f(x) = 1 - (1 - \frac{1}{x})^x\quad$という関数は収束が早そう
というわけでグラフ化
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(1, 101, 0.1)
y = 1 - (1 - (1/x)) ** x
plt.ylim([0.5, 1])
plt.title('$f(x) = 1-(1-\\frac{1}{x})^x$')
plt.xlabel('x')
plt.ylabel('f(x)', rotation=0)
plt.minorticks_on()
plt.grid(which="major", color="black", alpha=0.5)
plt.grid(which="minor", color="gray", linestyle=":")
plt.plot(x, y, c='red')
plt.show()
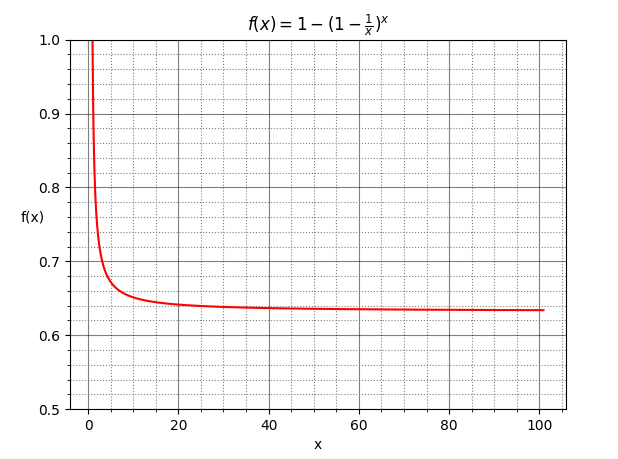
とりあえず$\quad x=101\quad$までプロット
グラフを見るに案の定収束が早い!
$x = 20\quad$の段階ですでに$0.64$ちょいに到達している
なので、$\frac{1}{n}$の確率の事象をn回試行した時に起こる確率は、だいたい63%くらいと言い切ってよさそう。
ギャンブルとかに使えそうだ