[Review] Long Short Term Memory in 1999

1999 version ~Learning to Forget~

Link: https://pdfs.semanticscholar.org/1154/0131eae85b2e11d53df7f1360eeb6476e7f4.pdf

Authors
Felix A. Gers
Jurgen Schmidhuber
Fred Cummins

Contents

1. Introduction
2. Standard LSTM
   1. Limits of standard LSTM
3. Solution: Forget Gates
   1. Forward Pass of Extended LSTM with Forget Gates
   2. Backward Pass of Extended LSTM with Forget Gates
   3. Complexity
4. Experiments
   1. Continual Embedded Reber Grammar Problem
   2. Network Topology and parameters
   3. CERG results
   4. Analysis of the CERG results
   5. Decreasing Learning Rate
   6. Continual Noisy Temporal Order Problem
5. Conclusion

Abstraction

Even though LSTM has overcome some issues which RNN could not, they have spotted some discovery on the weakness of LSTM, which is processing continual input streams that are not a priori segmented into subsequences with explicitly marked ends at which the network's internal state could be reset. But without reset, the state may grow infinitely and can cause the error in the network at the end. Hence, they have proposed a novel method, which is "forget gate" enabling an LSTM cell to learn to reset itself at adequate timing.

1. Introduction

Standard LSTM has some issue with updating of the cell states for continual sequence series. For example, if we feed the huge time series data, it will become saturate gradually and eventually this cause two problems described in section 2.1.

2. Standard LSTM

I have summarised in another post, so please check this!! https://qiita.com/Rowing0914/items/1edf16ead2190308ce90

2.1 Limits of standard LSTM

As it is described in section 1, very long and continual time series data certainly harms conventional LSTM, specifically we can claim two issues.

1. making $h$'s derivative vanish
2. making the cell output equal the output gate, which means the original RNN and BPTT
   And they have proposed that occasionally the internal state should reset.
   In order to come up with this idea, they had have tried many approaches, like weight decay, conventional backpropagation and another type of weight decay. However, none of them did work.

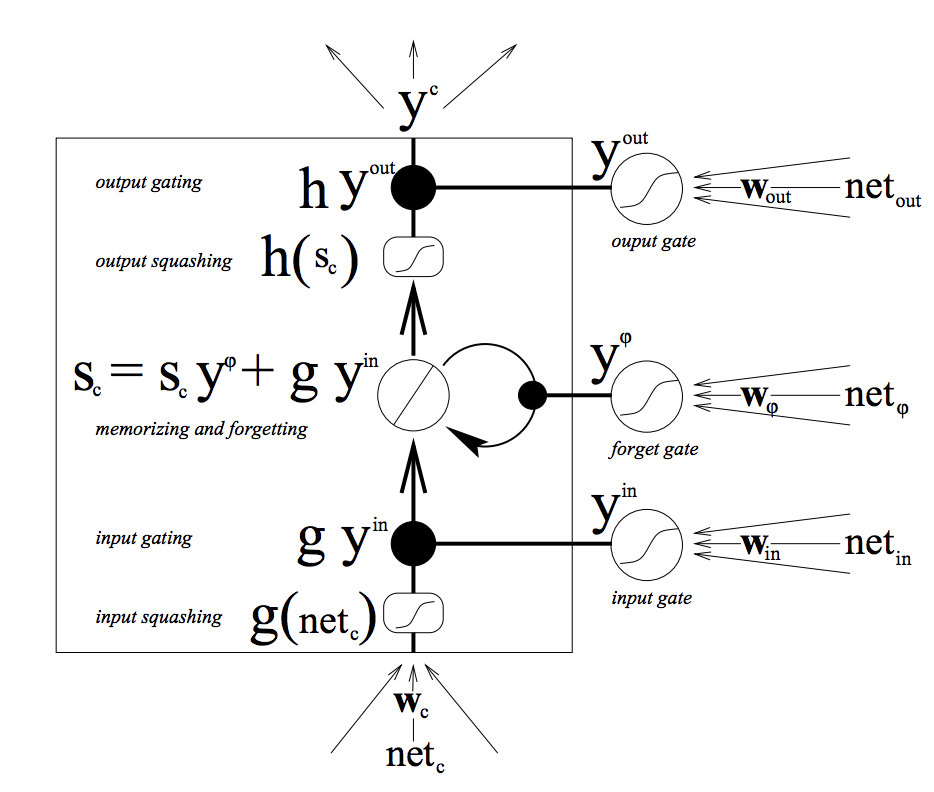
3. Solution: Forget Gates

1. Forward Pass of Extended LSTM with Forget Gates

• original cell state equation: only CEC(carrousel error constant)

S_{c^v_j}(0) = 0\\
S_{c^v_j}(t) = S_{c^v_j}(t-1) + y^{in_j}(t)g(net_{in_j}(t))

• forget gate adapted cell state: CEC + forget gate

S_{c^v_j}(0) = 0\\
S_{c^v_j}(t) = y^{\varphi}(t)S_{c^v_j}(t-1) + y^{in_j}(t)g(net_{in_j}(t))

2. Backward Pass of Extended LSTM with Forget Gates

First let us define the cost function.

E(t) = \frac{1}{2} \sum_k e_k(t)^2\\
e_k(t) := t^k(t) - y^k(t)

To minimise $E(t)$, we are going to use the gradient descent.

\Delta w_{lm} = - \alpha \frac{\partial E(t)}{\partial w_{lm}} = - \alpha \frac{\partial E(t)}{\partial y^k(t)} \frac{\partial y^k(t)}{\partial w_{lm}} = \alpha \sum_k e_k(t) \frac{\partial y^k(t)}{\partial w_{lm}}\\
=^{tr} \alpha \underbrace{ \sum_k e_k(t)  \frac{\partial y^k(t)}{\partial y^l(t)} \frac{\partial y^l(t)}{\partial net_l(t)}}_{=: \delta_l(t)} \underbrace{ \frac{\partial net_l(t)}{\partial w_{lm}}}_{y^m(t-1)}
\\
l=k\\
\delta_k(t) = e_k(t) f'_k(net_k(t)) \underbrace{ \frac{\partial y^k(t)}{\partial y^k(t)}}_{= 1}\\
l = i(hidden \space which \space is \space connected \space directly \space to the \space output\space layer)\\
\delta_i(t) = e_i(t) f'_i(net_i(t)) \underbrace{ \frac{\partial y^k(t)}{\partial y^i(t)}}_{= w_{ki} \delta_i(t)}\\
* \frac{\partial y^k(t)}{\partial y^l(t)}e_k(t) = \frac{\partial y^k(t)}{\partial net_k(t)} \frac{\partial net_k(t)}{\partial y^l(t)}e^k(t) = w_{kl} \underbrace{ \delta_l(t)}_{ f'_l(net_l(t))e^k(t)} \\
l = output \space gate\\
\frac{\partial y^{out_j}(t)}{\partial net^{out_j}(t)} = f'_{out_j}(net_{out_j}(t))\\
\frac{\partial y^{out_j}(t)}{\partial y^{out_j}(t)} e_k(t) = \frac{\partial y^{c^v_j}(t)}{\partial y^{out_j}(t)} \underbrace{ \frac{\partial y^k(t)}{\partial y^{c^v_j}(t)}e_k(t)}_{= w_{kc^v_j} \delta_k(t)} = h(s_{c^v_j}(t))w_{kc^v_j} \delta_k(t) \\
\delta^v_{out_j} = f'_{out_j}(net_{out_j}(t))h(s_{c^v_j}(t)) \big( \sum_kw_{kc^v_j} \delta_k(t) \big)\\

As every cell in a memory block contributes to the weight change of the output gate, we have to sum over all cells $v$ i block $j$ to obtain the total $\delta_{out_j}$ of the $j$-th memory block.

\delta_{out_j} = f'_{out_j}(net_{out_j}(t)) \biggl( \sum^{S_j}_{v=1} h(s_{c^v_j}(t)) \big( \sum_kw_{kc^v_j} \delta_k(t) \big) \biggl)

So far we have seen quit normal BPTT. For weights to cell, input gate and forget gate we adopt an RTRL-oriented perspective, by first stating the influence of a cell's internal state $s_{c^v_j}$ on the error and then analysing how each weight to the cell or the block's gates contributes to $s_{c^v_j}$.

\Delta_{lm}(t) = - \alpha \frac{\partial E(t)}{\partial w_{lm}} =^{tr} -\alpha \underbrace{ \frac{\partial E(t)}{\partial s_{c^v_j}(t)}}_{=: - e_{s_{c^v_j}}(t)} \frac{\partial s_{c^v_j}(t)}{\partial w_{lm}} = \alpha e_{s_{c^v_j}}(t) \frac{\partial s_{c^v_j}(t)}{\partial w_{lm}}\\
e_{s_{c^v_j}}(t) := - \frac{\partial E(t)}{\partial s_{c^v_j}(t)} =^{tr} - \frac{\partial E(t)}{\partial y^k(t)} \frac{\partial y^k(t)}{\partial y^{c^v_j}(t)} \frac{\partial y^{c^v_j}(t)}{\partial s_{c^v_j}(t)} = \frac{\partial y^{c^v_j}(t)}{\partial s_{c^v_j}(t)} \biggl( \sum_k \underbrace{ \frac{\partial y^k(t)}{\partial y^{c^v_j}(t)} e^k(t)}_{= w_{c^v_jl}\delta_k(t)} \biggl)\\
\frac{\partial y^{c^v_j}}{\partial s_{c^v_j}} = y^{out_j}(t)h'(s_{c^v_j}(t))
e_{s_{c^v_j}}(t) = y^{out_j}(t)h'(s_{c^v_j}(t))
e_{s_{c^v_j}}(t) \biggl( \sum_k w_{kc^v_j}\delta_k(t) \biggl)\\

Since the internal state composes three parts, which is input gate, forget gate and cell. Namely, $w_{lm}$ $l \in (\varphi, in, c^v_j)$. We are going to squash them into one equation!

\frac{\partial s_{c^v_j}(t)}{\partial w_{lm}} = \big( \delta_{in_jl} + \delta_{c^v_jl} + \delta_{\varphi_i} \big) \frac{\partial s_{c^v_j}(t-1)}{\partial w_{lm}}y^{\varphi_i}(t) + \delta_{c^v_jl} y^{in_j}(t) \frac{\partial g(net_{c^v_j(t)})}{\partial w_{lm}} + \delta_{in_j} g(net_{c^v_j}(t)) \frac{\partial y^{in_j}(t)}{\partial w_{lm}} + \delta_{\varphi} s_{c^v_j}(t-1) \frac{\partial y^{\varphi_j}(t)}{\partial w_{lm}}\\
\Delta w_{c^v_jm}(t) = \alpha e_{s_{c^v_j}}(t) \frac{\partial s_{c^v_j}}{\partial w_{c^v_jm}}\\

Nice summary

http://arunmallya.github.io/writeups/nn/lstm/index.html#/
http://karpathy.github.io/2015/05/21/rnn-effectiveness/
http://www.wildml.com/2015/10/recurrent-neural-network-tutorial-part-4-implementing-a-grulstm-rnn-with-python-and-theano/
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
https://gist.github.com/siemanko/b18ce332bde37e156034e5d3f60f8a23