LoginSignup
4
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

プログラミングゲームの解答コードを投稿しよう！
@RotterYkrn(ゆきりん)

【思い出の屋上】Sランク問題をBFSで解いたので、自分なりに解説する【電脳少女プログラミング2088 ─壊レタ君を再構築─】

Last updated at Posted at 2025-01-27

はじめに

　記事を書き始めた時点で、同じ解法の記事がなかったため、いい機会だと思って解説を書いてみます。ついさっき登録してこれが初投稿なので、お手柔らかにお願いします。

問題

【S Rank】思い出の屋上

概要

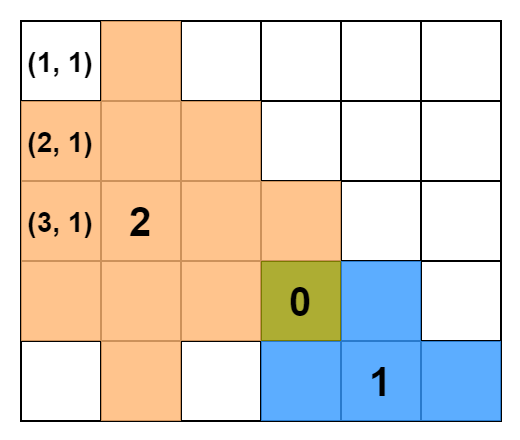
　$H \times W$グリッド上に$M$個の縄張りがあります。$i$番目の縄張りの範囲は、縄張りのサイズ$S_i$に対して、座標$(R_i,C_i)$からマンハッタン距離が$S_i$以下のすべてのマスです。
　すでにある縄張りに重ならないよう新たに縄張りを作るとき、縄張りのサイズ$S$としてあり得る最大値を求めます。

制約

  • $1 \leqq H,W \leqq 200$
  • $1 \leqq M \leqq 200$
  • $1 \leqq R_i \leqq H \quad (1 \leqq i \leqq M)$
  • $1 \leqq C_i \leqq W \quad (1 \leqq i \leqq M)$
  • $0 \leqq S_i \leqq 200 \quad (1 \leqq i \leqq M)$
  • 縄張り同士は重ならない

実装

考えたこと

　この問題の前に同ゲームのAランク問題でBFSを使用して、脳内がBFSに支配されていたので、「マンハッタン距離ってことはBFS使えるんじゃね？」となってBFSでの解法を考え始めました1。

　最終的な解法をざっくり説明すると、$H \times W$の配列を用意して、既に縄張りとして埋まっているマスを記録しておき、そのすぐ外側からBFSで空きマスを探索していったとき、探索距離の最大値が答えとなっています。

1. 既存の縄張りを記録する

　まず、$H \times W$のグリッドを表現するための配列を用意し、そこに各マスが縄張りとして使用されているかどうかを記録していきます。

　縄張りの情報は、中心の座標$(R,C)$とサイズ$S$で与えられるので、座標$(R,C)$を始点に、距離$S$以下の範囲でBFSを行えば、縄張りの記録ができます。（今回は、縄張りがあるマスを$1$としました。）

#include <bits/stdc++.h>
using namespace std;

// 上下左右
constexpr int dy[4] = {-1, 0, 1, 0};
constexpr int dx[4] = {0, 1, 0,-1};

// キューに保存する情報
struct State {
    // 座標:(r, c), 探索距離:d
    int r, c, d;
};

int main(void) {
    int H, W, M;
    cin >> H >> W >> M;
    vector<vector<int>> grid(H, vector<int>(W, 0));

    // 縄張り探索用のキュー
    queue<State> territory_que;
    for (int i = 0; i < M; i++) {
        int R, C, S;
        cin >> R >> C >> S;
        R--; C--;
        // キューに保存
        territory_que.push({R, C, S});
        grid[R][C] = 1;
    }

    // BFSで縄張りを記録
    while (!territory_que.empty()) {
        auto [r, c, d] = territory_que.front();
        territory_que.pop();

        for (int i = 0; i < 4; i++) {
            int nr = r + dy[i], nc = c + dx[i];
            if (0 <= nr && nr < H && 0 <= nc && nc < W && grid[nr][nc] != 1) {
                // dを減らしていき、0になったら終了
                if (d > 0) {
                    territory_que.push({nr, nc, d - 1});
                    grid[nr][nc] = 1;
                }
            }
        }
    }

    return 0;
}

2. 縄張りの外縁を保存する

　答えを探索する際に、縄張りの外縁をBFSの始点とする2ため、外縁の座標も保存しておく必要があります3。縄張りの記録と同時に行うと容易に実装できます。

// ...(省略)

int main(void) {

    // ...(省略)

+   // 答え探索用のキュー
+   queue<State> solution_que;
    // BFSで縄張りを記録
    while (!territory_que.empty()) {
        auto [r, c, d] = territory_que.front();
        territory_que.pop();

        for (int i = 0; i < 4; i++) {
            int nr = r + dy[i], nc = c + dx[i];
            if (0 <= nr && nr < H && 0 <= nc && nc < W && grid[nr][nc] != 1) {
                // dを減らしていき、0になったら終了
                if (d > 0) {
                    territory_que.push({nr, nc, d - 1});
                    grid[nr][nc] = 1;
+               } else {
+                   // 外縁の座標を保存
+                   solution_que.push({nr, nc, 0});
                }
            }
        }
    }

    return 0;
}

3. 空きマスを探索して答えを求める

　最後に、BFSで空きマスすべてを探索して答えを求めます。

　探索の始点を縄張りの外縁のマスすべてとし2、そこからの探索距離を記録しながら探索を進め、その中で一番長かった探索距離がこの問題の答えです。

　BFSは性質上、探索距離が一番短いものから処理されていくため、あるマスがキューに入れられた（あるいはキューから取り出された）ときに記録されている探索距離$d$は、(そのマスから一番近い縄張りマスまでのマンハッタン距離)$ - 1$になっています4。言い替えれば、そのマスからのマンハッタン距離が$d$以下のマスはすべて空きマスであり、かつ、そのような値の中で$d$が最大値となっているということです。

　BFSによって、すべての空きマスでそのような値$d$が求まるため、その中から$d$が最大であるマスを中心とすれば、グリッドの中で最大サイズの縄張りが作れます。

　（探索済みのマスを$2$としました。また、縄張りが1つも置けない場合は$-1$を出力しなければなりませんが、今回の実装では空きマスである場合のみansの入れ替えが発生するため、ansの初期値を$-1$としてそのまま出力すれば問題ありません。）

// ...(省略)

int main(void) {

    // ...(省略)
-               } else {
+               } else if (grid[nr][nc] != 2) {
                    // 外縁の座標を保存
                    solution_que.push({nr, nc, 0});
+                   // 外縁は探索済みにしておく
+                   grid[nr][nc] = 2;
                }
            }
        }
    }

+   int ans = -1;
+   // BFSで空きマスを探索
+   while (!solution_que.empty()) {
+       auto [r, c, d] = solution_que.front();
+       solution_que.pop();
+
+       // 外縁だが、他の縄張り内であるためスルー
+       if (grid[r][c] == 1) continue;
+
+       // 探索距離が長いものを保存
+       ans = max(ans, d);
+
+       for (int i = 0; i < 4; i++) {
+           int nr = r + dy[i], nc = c + dx[i];
+           if (0 <= nr && nr < H && 0 <= nc && nc < W && !grid[nr][nc]) {
+               solution_que.push({nr, nc, d + 1});
+               grid[nr][nc] = 2;
+           }
+       }
+   }
+
+   cout << ans << endl;

    return 0;
}

完成コード

#include <bits/stdc++.h>
using namespace std;

// 上下左右
constexpr int dy[4] = {-1, 0, 1, 0};
constexpr int dx[4] = {0, 1, 0,-1};

// キューに保存する情報
struct State {
    // 座標:(r, c), 探索距離:d
    int r, c, d;
};

int main(void) {
    int H, W, M;
    cin >> H >> W >> M;
    vector<vector<int>> grid(H, vector<int>(W, 0));

    // 縄張り探索用のキュー
    queue<State> territory_que;
    for (int i = 0; i < M; i++) {
        int R, C, S;
        cin >> R >> C >> S;
        R--; C--;
        // キューに保存
        territory_que.push({R, C, S});
        grid[R][C] = 1;
    }

    // 答え探索用のキュー
    queue<State> solution_que;
    // BFSで縄張りを記録
    while (!territory_que.empty()) {
        auto [r, c, d] = territory_que.front();
        territory_que.pop();

        for (int i = 0; i < 4; i++) {
            int nr = r + dy[i], nc = c + dx[i];
            if (0 <= nr && nr < H && 0 <= nc && nc < W && grid[nr][nc] != 1) {
                // dを減らしていき、0になったら終了
                if (d > 0) {
                    territory_que.push({nr, nc, d - 1});
                    grid[nr][nc] = 1;
                } else if (grid[nr][nc] != 2) {
                    // 外縁の座標を保存
                    solution_que.push({nr, nc, 0});
                    // 外縁は探索済みにしておく
                    grid[nr][nc] = 2;
                }
            }
        }
    }

    int ans = -1;
    // BFSで空きマスを探索
    while (!solution_que.empty()) {
        auto [r, c, d] = solution_que.front();
        solution_que.pop();

        // 外縁だが、他の縄張り内であるためスルー
        if (grid[r][c] == 1) continue;

        // 探索距離が長いものを保存
        ans = max(ans, d);

        for (int i = 0; i < 4; i++) {
            int nr = r + dy[i], nc = c + dx[i];
            if (0 <= nr && nr < H && 0 <= nc && nc < W && !grid[nr][nc]) {
                solution_que.push({nr, nc, d + 1});
                grid[nr][nc] = 2;
            }
        }
    }

    cout << ans << endl;

    return 0;
}

計算量 （2025/1/31 訂正）

　縄張り内のマスを各1回、空きマスを各1回訪問するため、結果グリッド内のすべてのマスを1回ずつ訪問することになり、$\Theta(HW)$。

正確には......

　まず、上記の通りすべてのマスは、必ず1回はキューへの追加・取り出しが行われます。

　ですが、今回の実装では、「あるマスを縄張りの外縁としてキューに入れたが、実は別の縄張り範囲内だった」という状況になる場合があります。その場合そのマスは、縄張り探索時と、答え探索時で、キューへの追加・取り出しが計2回行われることになります。

　そのようなマスの数を$C$とすると、探索回数は、

HW + C

となります。

　ここで、$C$が取り得る値を考えると、$HW$を超えることはないことがわかります。

　したがって、

HW \leqq 探索回数 \leqq 2HW

となり、全体の計算量は$\Theta (HW)$となります。

余談

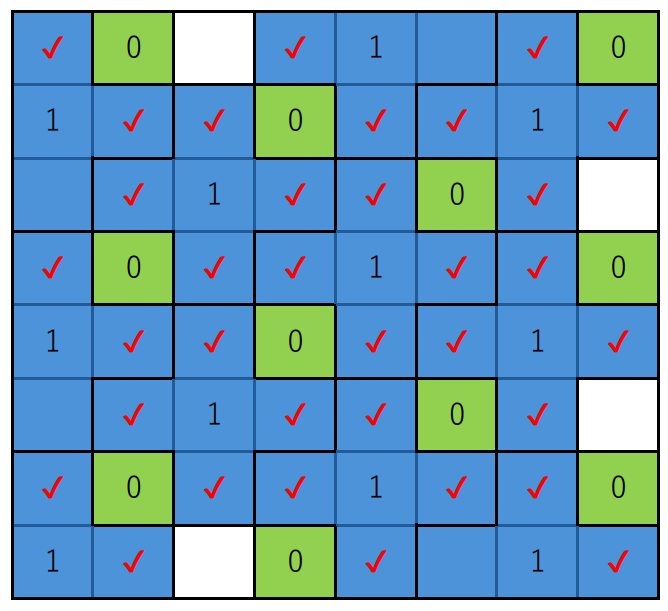
　本制約を踏まえると、$C$の上限は$HW$よりも小さい値で抑えられるでしょう。私自身が考えた限りでは、以下のような配置で最大となり、$\displaylines{C < \frac{2}{3}HW}$程度に抑えられました。（✔が入っている箇所が、探索が2回行われるマス。）

image.png

（訂正前）

解説用に書き直す前のコードでは以下のような状況が発生し得たのですが、本記事のコードでは解消されています。

　ここで、$C$が取り得る値を考えると、$0 \leqq C \leqq HW - 1$であることがわかります。（グリッドのすべてのマスにサイズ$0$の縄張りが設置され、左上のものから順番に番号が付けられていた場合に最大となります。）5

レイミの評価（ツンデレ系）

上記のコードを提出した結果↓

　実は最初に提出したものは、実装に使ったアルゴリズムなんかは褒めてもらえましたが、雑に変数名を付けたり、コメントが皆無だったりしたので、コメントの後半でその部分を指摘されていました。

　ですが、解説用に書き直したバージョンではもう今までにないくらいべた褒めされてしまいました。なんだかんだ褒められるとちょっと嬉しいものです。

　上のコメントはツンデレ系ですが、本ゲームには他にも「元気系」や「クール系」などの多種多様な性格が全部で18種類あり、見た目も含めて自由にカスタマイズできるため、ぜひ自分の手でゲームをプレイし、いろいろな性格のコードレビューを受けてみてはいかがでしょうか6。

あとがき

　ちょっと飽き性で、競プロの過去問とかやっていても集中がすぐ途切れちゃうんですが、ゲームだと全然疲れないで最後までやってしまいました。
　あとBFSとかの探索系アルゴリズムを実装するのすごい楽しい。

  1. そもそも座標を使ってマンハッタン距離の問題を解くと、条件文が複雑になるイメージがあって少し苦手なんですよね…… ↩

  2. 今回の制約下では、縄張りの範囲がグリッドの外にはみ出しても問題ないため、外縁からの距離のみを考えればよい。 ↩ ↩2

  3. 新しい縄張りの中心を外縁に設置することを考えると、その縄張りのサイズは$0$となるため、外縁の探索距離は$0$として保存する。 ↩

  4. 縄張りの外縁を$0$としたため。 ↩

  5. なんで数式に打ち消し線入らないの…… ↩

  6. ちなみに私は、ツンデレっぽい見た目に近づけようと試行錯誤していたら、見た目が完全にラブ〇イブ！のに〇にーになっていて笑いました。 ↩

4
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?