AtCoderログ：0044 - ARC 124 A

問題

問題文

$N$ 枚のカードが左から右に並んでいます。 各カードに $1$ 以上 $K$ 以下の整数を書き込みます。はじめ、どのカードにも整数は書かれていません。
$1$ から $K$ の番号がついた $K$ 個の制約が与えられます。制約 $i$ は文字 $c_i$ と整数 $k_i$ からなります。$c_i$ が L ならば、$i$ が書かれたカードのうち最も 左 にあるものは $N$ 枚のカードのうち左から $k_i$ 番目である必要があります。$c_i$ が R ならば、$i$ が書かれたカードのうち最も 右 にあるものは $N$ 枚のカードのうち左から $k_i$ 番目である必要があります。
$1$ 以上 $K$ 以下の各整数 $i$ について、$i$ が書かれたカードが少なくとも $1$ つ存在する必要があることに注意してください。
上記の $K$ 個の制約をすべて満たすようなカードへの整数の書き込み方の個数を $998244353$ で割ったあまりを求めてください。

制約

・$1 \le N, K \le 1000$
・$c_i$ は L, R のいずれか
・$1 \le k_i \le N$
・$i \ne j$ ならば $k_i \ne k_j$

回答

回答1 (AC)

$N$ 枚のカードのそれぞれに $1$ から $K$ までの整数のいずれかが書き込まれるので、最初の段階で、各カードの値の可能性は $K$ 通りずつあります。そこで $K$ 行 $N$ 列の表を用いて、各カードの値の可能性を調べていくことにします。$i$ 行目は数字 $i$ を書き込む列を表します。

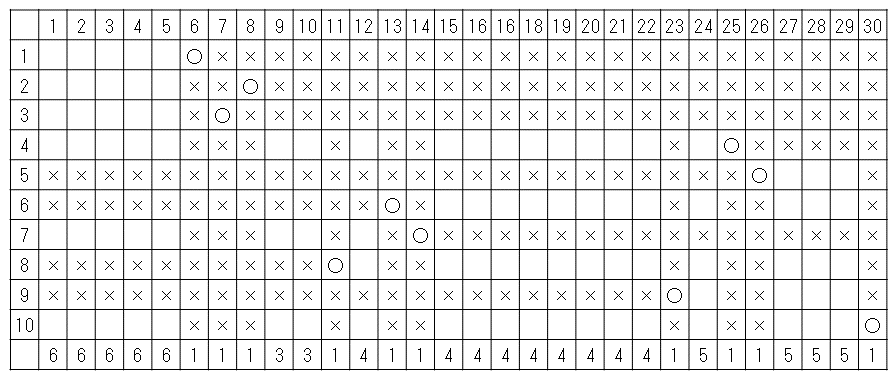
例として入力例2を使用しましょう。1 番目の制約条件は「R 6」なので、1 行目の左から 6 番目は $1$ を書き込むことを表すために「○」をかき、さらに左から 7 番目以降には $1$ が書き込まれる可能性がないことを表すために「×」をつけていきます。2 番目の制約条件は「R 7」なので、2 行目の左から 7 番目には「○」をかき、8 番目以降には「×」をつけていきます。全ての制約条件に対してこの作業を繰り返した結果が下表になります。

この表より、1 番目のカードに書き込まれる値は $1, 2, 3, 4, 7, 10$ の 6 通り、2 番目のカードに書き込まれる値も $1, 2, 3, 4, 7, 10$ の 6 通りであることがわかるので、1 番目と 2 番目のカードに書き込まれる数字のパターンは $6 \times 6=36$ 通りとなります。同様にして全てのカードについて調べると、30 枚のカードに書き込まれる数字のパターンは
$$
6 \times 6 \times 6 \times 6 \times 6 \times
1 \times 1 \times 1 \times 3 \times 3 \times
1 \times 4 \times 1 \times 1 \times 4 \times
4 \times 4 \times 4 \times 4 \times 4 \times
4 \times 4 \times 1 \times 5 \times 1 \times
1 \times 5 \times 5 \times 5 \times 1 = 11466178560000
$$
通りとなり、これを $998244353$ で割って、余り $343921442$ を得ます。この操作をコードにすると以下のようになります。

arc124a-1.cpp

#include <bits/stdc++.h>
using namespace std;

int main() {
  int N, K;
  cin >> N >> K;

  vector<vector<int>> m(K+1,vector<int>(N+1,1));
  string c;
  int k;
  for ( int i=1; i<=K; i++ ) {
    cin >> c >> k;
    if ( c=="L" ) {
      for ( int j=1; j<k; j++ ) {
        m.at(i).at(j) = 0;
      }
    } else {
      for ( int j=k+1; j<=N; j++ ) {
        m.at(i).at(j) = 0;
      }
    }      
    for ( int ii=1; ii<=K; ii++ ) {
      if ( ii!=i ) {
        m.at(ii).at(k) = 0;
      }
    }
  }

  int64_t answer = 1, MOD = 998244353;
  for ( int j=1; j<=N; j++ ) {
    int sum = 0;
    for ( int i=1; i<=K; i++ ) {
      sum += m.at(i).at(j);
    }
    answer = answer*sum%MOD;
  }

  cout << answer << endl;
}

回答2 (AC)

回答1を再考してみると、最終的には各列の値の可能性をかけていけばよく、具体的に取り得る値までを管理する必要はありません。ここである列の値の可能性に変化が生じるのは、(1)どこかの列で L または R に関する処理をおこなったときで、列の値の可能性は1通り減ることがある、(2)その列のどこかの行で値が確定したときで、列の値の可能性は1通りになる、のいずれかです。そこで各列の値の可能性だけを管理することで、処理を簡略化することが可能になります。ただし、(2)の処理で値を 1 した列から (1)の処理でさらに 1 を減じることのないように注意が必要になります。コードは以下のようになりました。

abc047b-2.cpp

#include <bits/stdc++.h>
using namespace std;

int main() {
  int n, k;
  cin >> n >> k;

  vector m(n+1,k);
  string c;
  int p;
  for ( int i=1; i<=k; i++ ) {
    cin >> c >> p;
    if ( c=="L" ) {
      for ( int j=1; j<p; j++ ) {
        if ( m.at(j)>2 ) {
          m.at(j) -= 1;
        }
      }
    } else {
      for ( int j=p+1; j<=n; j++ ) {
        if ( m.at(j)>2 ) {
          m.at(j) -= 1;
        }
      }
    }
    m.at(p) = 1;
  }

  int64_t answer = 1, MOD = 998244353;
  for ( int j=1; j<=n; j++ ) {
    answer = answer*m.at(j)%MOD;
  }

  cout << answer << endl;
}

調べたこと

AtCoder の解説 → 公式解説

回答2と同じ方針ですが、それぞれの制約条件ごとに値の可能性を増やす戦略をとることで処理が簡単になるようでした。

リンク

• 前の記事 → AtCoderログ：0043 - ABC 175 B
• 次の記事 → AtCoderログ：0045 - ABC 083 B