この記事はISer Advent Calendar 2019の21日目として書かれたものです。
はじめに
この記事ではG3Cと呼ばれる古典命題論理のシークエント計算を用いた自動証明を実装します。とはいえ、厳密な理論にはあまり踏み込まず実装をメインに書いていくつもりです。この記事で作るものは例えば$$
\lnot P \lor Q \Rightarrow P \to Q
$$というシークエントを入力として与えると
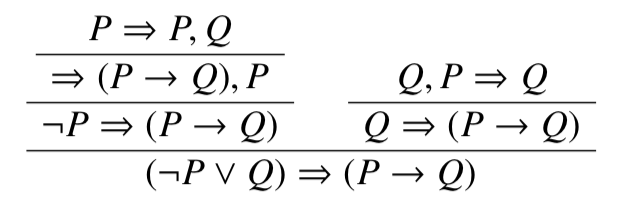
というように証明図を出力してくれます。証明の体系はシークエント計算以外にもいくつかありますが、シークエント計算はこのような自動証明を簡単に行えるものとして知られています。よって、今回はこれを実装してみようと思います。
シークエント計算とは
シークエント
シークエントとは簡単に言えば命題です。例えば
$$
A,B \Rightarrow C,D
$$
というシークエントは「AとBが共に真であれば、CとDのうち少なくとも一つは真である」という命題を表します。この命題が正しいとき、このシークエントは**トートロジー(恒真)**であると言うことにします。
例えば、次のシークエントはトートロジーであると言えます。$$
A \to B \Rightarrow \lnot A, B
$$「AならばB」が真なら「Aでない」または「Bである」が成り立ちます。なぜ成り立つかというとシークエント計算の証明系を用いて証明することができるからです。この命題については直感的に正しいと思われる方も多いと思いますが、シークエント計算の証明系はそのような直感に反しないように作られています。
論理記号
先ほどの命題では論理記号として$\lnot$と$\to$が出てきました。命題論理の論理記号は4種類だけです。それらは直感的な意味と一致しています。
| 記号 | 例 | 意味 |
|---|---|---|
| $\lnot$ | $\lnot A$ | Aでない |
| $\land$ | $A\land B$ | AかつB |
| $\lor$ | $A\lor B$ | AまたはB |
| $\to$ | $A \to B$ | AならばB |
推論規則
証明を行うには推論ができなければいけません。推論は次のような形で表します。
$$
\cfrac{A \Rightarrow B}{C \Rightarrow D}
$$
これは$A \Rightarrow B$というシークエントがトートロジーなら$C \Rightarrow D$というシークエントもトートロジー 、つまり$A \Rightarrow B$から$C \Rightarrow D$が導けるということを表します。
G3Cの証明系では以下の8種類の推論規則が定められています。証明はこの8種類の推論規則を使って組み立てていくことになります。なお、シークエントの各辺で論理式の順番は任意に入れ替えられるものとします。
$$
\cfrac{\Gamma \Rightarrow \Delta , A}{\lnot A, \Gamma \Rightarrow \Delta}(\lnot左)
\qquad
\cfrac{A,\Gamma \Rightarrow \Delta}{\Gamma \Rightarrow \Delta, \lnot A}(\lnot右)
$$$$
\cfrac{A,B,\Gamma \Rightarrow \Delta}{A \land B,\Gamma \Rightarrow \Delta}(\land左)
\qquad
\cfrac{\Gamma \Rightarrow \Delta,A \quad \Gamma \Rightarrow \Delta,B}{\Gamma \Rightarrow \Delta,A \land B}(\land右)
$$$$
\cfrac{A,\Gamma \Rightarrow \Delta \quad B,\Gamma \Rightarrow \Delta}{A \lor B,\Gamma \Rightarrow \Delta}(\lor左)
\qquad
\cfrac{\Gamma \Rightarrow \Delta,A,B}{\Gamma \Rightarrow \Delta,A \lor B}(\lor 右)
$$$$
\cfrac{\Gamma \Rightarrow \Delta,A \quad B,\Gamma \Rightarrow \Delta}{A \to B, \Gamma \Rightarrow \Delta}(\to左)
\qquad
\cfrac{A,\Gamma \Rightarrow \Delta,B}{\Gamma \Rightarrow \Delta, A \to B}(\to 右)
$$
これらの推論規則は直感的に納得できるものとなっています。例えば「$\lnot$左」の推論を見てみましょう。
いま$\Gamma$を仮定すれば$\Delta$または$A$が成り立つことが分かっています。
(i)$\Gamma$から$\Delta$が導けるなら当然$\lnot A, \Gamma \Rightarrow \Delta$は恒真です。
(ii)$\Gamma$から$A$が導けるなら$\lnot A, \Gamma$が共に真となることはないので、右辺に関わらず$\lnot A, \Gamma \Rightarrow \Delta$は恒真です。
他の推論規則については書きませんがこのように考えて納得することができると思います。
開始シークエント
さて、前述の推論規則を組み合わせて証明を行なっていくわけですが、そのためには証明図の一番上に位置する公理となるシークエントが必要です。これを開始シークエントと呼びます。これは誰が見ても自明に真となるようなシークエントでなければなりません。恒真なシークエントから導けるシークエントはまた恒真であるというわけです。
ここで扱う証明系における開始シークエントは以下の形をしたものだけです。
$$
P,\Gamma \Rightarrow P,\Delta
$$
$P,\Gamma$が共に真なら$P,\Delta$の少なくとも1つは真である。$P$が真なのだから当たり前ですね。
証明
証明すべきシークエントが与えられたときに、開始シークエントから推論規則を繰り返し適用して最終的に与えられたシークエントに一致すれば証明ができたことになります。
例として、一番最初にあげたシークエント
$$
A \to B \Rightarrow \lnot A, B
$$
をこの規則に従って証明してみます。以下がその証明になります。
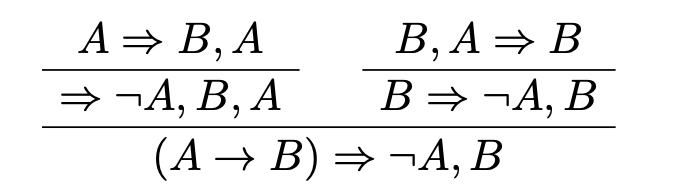
この証明図を自動で書くのが今回の目標になります。
証明探索のアルゴリズム
シークエントの大きさ
証明探索のアルゴリズムを紹介する前にシークエントの大きさという概念を導入しておきます。大きさとはシークエントに含まれる論理記号$\lnot,\land,\lor,\to$の総数です。
例えば
$$
A \to B \Rightarrow \lnot A, B
$$
というシークエントには$\to$と$\lnot$が1つずつ含まれているので大きさは2となります。
さて、大きさに着目して推論規則をもう一度眺めてみましょう。どの推論規則においても線の下のシークエントの大きさは上のシークエントの大きさより1だけ大きくなっているのが分かると思います。これが証明探索のポイントになります。
大きさ0のシークエント
証明は基本的に公理から結論を導くのですから上から下に証明図を書いていくのが自然です。ところが証明探索では証明すべきシークエントが与えられたときに、それを一番下として下から上に探索を行います。証明図を1段上に辿れば大きさが1小さくなるわけですから、証明すべきシークエントがどんなものだったとしても、推論規則を繰り返し適用すればいずれは大きさ0のシークエントの集合に帰着します。大きさ0のシークエントはこれ以上変形のしようがないので、開始シークエントであるかどうかをみるだけでそれが恒真であるかを判定できます。
アルゴリズム
証明探索のアルゴリズムは「ワングのアルゴリズム」とも呼ばれます。何やら良い感じの名前ですが考え方は極めて自然です。特に新しいことはありません。与えられたシークエントを大きさ0のシークエントに帰着させ、それらが全て開始シークエントなら元のシークエントは証明可能であり、1つでも開始シークエントでないものがあれば証明可能ではありません。以下に詳しく書いておきます。基本的には与えられたシークエントがトートロジーかどうかを判定するアルゴリズムですが、少し工夫すれば証明図を書くこともできます。
いま $\Gamma \Rightarrow \Delta$ というシークエントが与えられたとします。まず最初にこのシークエントの大きさが0であるかどうかを調べます。0であるならそれがイニシャル・シークエントかどうかを判断することでトートロジーかどうかを判定できます。
大きさが1以上なら$\Gamma \Rightarrow \Delta$は論理記号$\lnot,\land,\lor,\to$を必ず含んでいます。それを左から探索して論理記号が見つかったら、推論規則を下から上にたどることで大きさが1小さい1つまたは2つのシークエントが得られます。同様にそれらのシークエントがトートロジーであるかどうかを判定します。この操作を繰り返せば最終的に大きさ0のシークエントに帰着し、再帰的に$\Gamma \Rightarrow \Delta$がトートロジーであるかどうかを判定することができます。
長くなってしまいましたが、基本的な考え方は単純です。これからこのアルゴリズムを実装していきます。
証明探索の実装
ここではPython3で実装します。コード全体はこの記事の最後に載せるとして、ここでは重要な部分だけコードを書いておきます。
クラスを3つ定義することを考えます。
- AtomicFormula(原子命題)
- Formula(論理式)
- Sequent(シークエント)
1. AtomicFormula
$P,Q$などのこれ以上分割できない命題です。
class AtomicFormula:
def __init__(self, name):
self.name = name
def is_atomic(self):
return True
名前だけを持ちます。is_atomicは今後使うので定義しておきます。
2. Formula(論理式)
論理式には $P \to Q, \quad \lnot(S \land T),\quad P \to ((P \land Q) \lor (S \land T))$ など様々なものがありますが、その階層構造に着目すると最も外側では
- $\lnot A$
- $A\land B$
- $A\lor B$
- $A\to B$
のいずれかの形になっていることが分かります。これをもとに定義します。
class Formula:
def __init__(self, relation, form1, form2=None):
self.relation = relation
self.form1 = form1
self.form2 = form2
def is_atomic(self):
return False
self.relationは$\lnot,\land,\lor,\to$に対してそれぞれ1,2,3,4と定めることにします。また、上記の$A$をform1、$B$をform2として、やはりis_atomicを定義しておきます。
3. Sequent(シークエント)
シークエントは$\Rightarrow$の左右に論理式の列を持ちます。証明図の探索はこのクラスのメソッドとして定義します。
class Sequent:
def __init__(self, Left, Right):
self.Left = Left
self.Right = Right #Left, RightはFormula, AtomicFormulaのリスト
# 開始シークエント判定
def is_initial(self):
for l in self.Left:
if l in self.Right: return True
return False
# 大きさ0のシークエント判定
def is_atomic(self):
for l in self.Left:
if not l.is_atomic(): return False
for r in self.Right:
if not r.is_atomic(): return False
return True
# トートロジー判定
def is_tautology(self):
if self.is_atomic():
return self.is_initial()
for l in range(len(self.Left)):
if not self.Left[l].is_atomic():
self.Left[0],self.Left[l]=self.Left[l],self.Left[0]
form = self.Left[0]
if form.relation==1:
return Sequent(self.Left[1:], self.Right+[form.form1]).is_tautology()
if form.relation==2:
return Sequent(self.Left[1:]+[form.form1,form.form2], self.Right).is_tautology()
if form.relation==3:
return Sequent(self.Left[1:]+[form.form1], self.Right).is_tautology() and Sequent(self.Left[1:]+[form.form2], self.Right).is_tautology()
if form.relation==4:
return Sequent(self.Left[1:], self.Right+[form.form1]).is_tautology() and Sequent(self.Left[1:]+[form.form2], self.Right).is_tautology()
for r in range(len(self.Right)):
if not self.Right[r].is_atomic():
self.Right[0],self.Right[r]=self.Right[r],self.Right[0]
form=self.Right[0]
if form.relation==1:
return Sequent(self.Left+[form.form1], self.Right[1:]).is_tautology()
if form.relation==2:
return Sequent(self.Left, self.Right[1:]+[form.form1]).is_tautology() and Sequent(self.Left, self.Right[1:]+[form.form2]).is_tautology()
if form.relation==3:
return Sequent(self.Left, self.Right[1:]+[form.form1,form.form2]).is_tautology()
if form.relation==4:
return Sequent(self.Left+[form.form1], self.Right[1:]+[form.form2]).is_tautology()
def prooftree(self):
#後で書きます
is_tautologyではワングのアルゴリズムと推論規則をそのまま実装しています。Left,Rightの最初の要素がatomicならatomicでない要素と入れ替えた上で、最初の要素に対して推論規則を適用しています。
これで任意のシークエントについてis_tautologyメソッドを呼ぶことで証明可能かどうかを判定できるようになりました。ちなみにこの定義では例えば
$$
A \to B \Rightarrow \lnot A, B
$$
は
Sequent([Formula(4, AtomicFormula('A'), AtomicFormula('B'))], [Formula(1, AtomicFormula('A')), AtomicFormula('B')])
と表されていることに注意してください。この変換を行うコードは後回しにすることにします。
それではprooftree、すなわち証明図を書くメソッドに取り掛かるのですが、証明図を書くためにLaTeXのprooftree環境を使います。使い方は簡単なのでこちらのサイトなどを眺めると良いと思います。prooftreeメソッドはこの環境に渡すコードを返すものとして作ります。
この環境では証明図の1つの枝を書けるところまで書いて、書けなくなったら別の枝に行ってそして統合するというような書き方をします。何が言いたいかというと証明探索とちょうど逆の順番で証明図を書いています。この事実によって証明図を書くのが非常に楽になります。探索の過程でどんどん前に付け足していけば良いのです。以下がprooftreeの定義ですがis_tautologyとほとんど変わりません。
def prooftree(self):
if self.is_atomic(): return '\\AxiomC'+str(self)
string = str(self)
for l in range(len(self.Left)):
if not self.Left[l].is_atomic():
self.Left[0],self.Left[l]=self.Left[l],self.Left[0]
form = self.Left[0]
if form.relation==1:
return Sequent(self.Left[1:], self.Right+[form.form1]).prooftree()+'\n'+'\\UnaryInfC'+string
if form.relation==2:
return Sequent(self.Left[1:]+[form.form1,form.form2], self.Right).prooftree()+'\n'+'\\UnaryInfC'+string
if form.relation==3:
return Sequent(self.Left[1:]+[form.form1], self.Right).prooftree() + Sequent(self.Left[1:]+[form.form2], self.Right).prooftree() +'\n'+'\\BinaryInfC'+string
if form.relation==4:
return Sequent(self.Left[1:], self.Right+[form.form1]).prooftree() + Sequent(self.Left[1:]+[form.form2], self.Right).prooftree() + '\n'+'\\BinaryInfC'+string
for r in range(len(self.Right)):
if not self.Right[r].is_atomic():
self.Right[0],self.Right[r]=self.Right[r],self.Right[0]
form=self.Right[0]
if form.relation==1:
return Sequent(self.Left+[form.form1], self.Right[1:]).prooftree()+'\n'+'\\UnaryInfC'+string
if form.relation==2:
return Sequent(self.Left, self.Right[1:]+[form.form1]).prooftree() + Sequent(self.Left, self.Right[1:]+[form.form2]).prooftree()+'\n'+'\\BinaryInfC'+string
if form.relation==3:
return Sequent(self.Left, self.Right[1:]+[form.form1,form.form2]).prooftree()+'\n'+'\\UnaryInfC'+string
if form.relation==4:
return Sequent(self.Left+[form.form1], self.Right[1:]+[form.form2]).prooftree()+'\n'+'\\UnaryInfC'+string
最後に$\lnot,\land,\lor,\to$を使って書かれた論理式(シークエントではない)をクラスの入れ子に変換する関数を定義しておきます。シークエントを論理式に分けるのは簡単なので省略します。なお、論理記号の優先順位は$\lnot$が最も高く、それ以外は同等と想定しています。実装は最も外側の階層の論理記号をなんとかして見つけようとしています。
def read(exp):
if '¬' in exp or '∧' in exp or '∨' in exp or '→' in exp:
#()の外にある論理記号を見つける
i=len(exp)-1
if exp[i]==')':
c=1
while c:
i-=1
if exp[i]=='(': c-=1
elif exp[i]==')': c+=1
if i==0:
return read(exp[1:-1])
while exp[i] not in ['∧' , '∨' , '→']:
if i==0 and exp[i]=='¬':
return Formula(1, read(exp[1:]))
i-=1
if exp[i]=='∧': return Formula(2, read(exp[:i]), read(exp[i+1:]))
elif exp[i]=='∨': return Formula(3, read(exp[:i]), read(exp[i+1:]))
elif exp[i]=='→': return Formula(4, read(exp[:i]), read(exp[i+1:]))
return AtomicFormula(exp)
長くなりましたが実装はこれで終わりです。最後に全コードを載せていますので皆さんもぜひいろいろなシークエントを入力して試してみてください。
終わりに
ここまで読んでくださってありがとうございます。初めての記事で説明が不親切な部分もあったかと思います。説明が不正確なところもあるかもしれません。いろいろとご指摘をいただければ幸いです。
今回書いたコードは全体でも200行足らずということで、シークエント計算を使えば簡単に自動証明を作れるということがわかってもらえたと思います。もちろん他の方法でも自動化することはできるので、自然演繹などでもやってみると面白いかもしれません。それでは最後に全コードを載せておきます。
全コード
# -*- coding: utf-8 -*-
import sys
class AtomicFormula:
def __init__(self, name):
self.name = name
def is_atomic(self):
return True
def __eq__(self, other):
if type(other) != AtomicFormula: return False
return self.name == other.name
def __str__(self):
return self.name
class Formula:
def __init__(self, relation, form1, form2=None):
self.relation = relation
# 1:not
# 2:and
# 3:or
# 4:->
self.form1 = form1
self.form2 = form2
def is_atomic(self):
return False
def __eq__(self, other):
if type(other) != Formula: return False
return self.relation==other.relation and self.form1==other.form1 and self.form2==other.form2
def __str__(self):
if self.relation==1: return '\\lnot '+str(self.form1)
if self.relation==2: return '('+str(self.form1)+'\\land '+str(self.form2)+')'
if self.relation==3: return '('+str(self.form1)+'\\lor '+str(self.form2)+')'
if self.relation==4: return '('+str(self.form1)+'\\to '+str(self.form2)+')'
class Sequent:
def __init__(self, Left, Right):
self.Left = Left
self.Right = Right
def is_initial(self):
for l in self.Left:
if l in self.Right: return True
return False
def is_atomic(self):
for l in self.Left:
if not l.is_atomic(): return False
for r in self.Right:
if not r.is_atomic(): return False
return True
def is_tautology(self):
if self.is_atomic():
return self.is_initial()
for l in range(len(self.Left)):
if not self.Left[l].is_atomic():
self.Left[0],self.Left[l]=self.Left[l],self.Left[0]
form = self.Left[0]
if form.relation==1:
return Sequent(self.Left[1:], self.Right+[form.form1]).is_tautology()
if form.relation==2:
return Sequent(self.Left[1:]+[form.form1,form.form2], self.Right).is_tautology()
if form.relation==3:
return Sequent(self.Left[1:]+[form.form1], self.Right).is_tautology() and Sequent(self.Left[1:]+[form.form2], self.Right).is_tautology()
if form.relation==4:
return Sequent(self.Left[1:], self.Right+[form.form1]).is_tautology() and Sequent(self.Left[1:]+[form.form2], self.Right).is_tautology()
for r in range(len(self.Right)):
if not self.Right[r].is_atomic():
self.Right[0],self.Right[r]=self.Right[r],self.Right[0]
form=self.Right[0]
if form.relation==1:
return Sequent(self.Left+[form.form1], self.Right[1:]).is_tautology()
if form.relation==2:
return Sequent(self.Left, self.Right[1:]+[form.form1]).is_tautology() and Sequent(self.Left, self.Right[1:]+[form.form2]).is_tautology()
if form.relation==3:
return Sequent(self.Left, self.Right[1:]+[form.form1,form.form2]).is_tautology()
if form.relation==4:
return Sequent(self.Left+[form.form1], self.Right[1:]+[form.form2]).is_tautology()
def prooftree(self):
if self.is_atomic(): return '\\AxiomC'+str(self)
string = str(self)
for l in range(len(self.Left)):
if not self.Left[l].is_atomic():
self.Left[0],self.Left[l]=self.Left[l],self.Left[0]
form = self.Left[0]
if form.relation==1:
return Sequent(self.Left[1:], self.Right+[form.form1]).prooftree()+'\n'+'\\UnaryInfC'+string
if form.relation==2:
return Sequent(self.Left[1:]+[form.form1,form.form2], self.Right).prooftree()+'\n'+'\\UnaryInfC'+string
if form.relation==3:
return Sequent(self.Left[1:]+[form.form1], self.Right).prooftree() + Sequent(self.Left[1:]+[form.form2], self.Right).prooftree() +'\n'+'\\BinaryInfC'+string
if form.relation==4:
return Sequent(self.Left[1:], self.Right+[form.form1]).prooftree() + Sequent(self.Left[1:]+[form.form2], self.Right).prooftree() + '\n'+'\\BinaryInfC'+string
for r in range(len(self.Right)):
if not self.Right[r].is_atomic():
self.Right[0],self.Right[r]=self.Right[r],self.Right[0]
form=self.Right[0]
if form.relation==1:
return Sequent(self.Left+[form.form1], self.Right[1:]).prooftree()+'\n'+'\\UnaryInfC'+string
if form.relation==2:
return Sequent(self.Left, self.Right[1:]+[form.form1]).prooftree() + Sequent(self.Left, self.Right[1:]+[form.form2]).prooftree()+'\n'+'\\BinaryInfC'+string
if form.relation==3:
return Sequent(self.Left, self.Right[1:]+[form.form1,form.form2]).prooftree()+'\n'+'\\UnaryInfC'+string
if form.relation==4:
return Sequent(self.Left+[form.form1], self.Right[1:]+[form.form2]).prooftree()+'\n'+'\\UnaryInfC'+string
def __str__(self):
return '{$'+','.join(map(str,self.Left))+'\Rightarrow '+','.join(map(str,self.Right))+'$}'
def read(exp):
if '¬' in exp or '∧' in exp or '∨' in exp or '→' in exp:
#()の外にある論理記号を見つける
i=len(exp)-1
if exp[i]==')':
c=1
while c:
i-=1
if exp[i]=='(': c-=1
elif exp[i]==')': c+=1
if i==0:
return read(exp[1:-1])
while exp[i] not in ['∧' , '∨' , '→']:
if i==0 and exp[i]=='¬':
return Formula(1, read(exp[1:]))
i-=1
if exp[i]=='∧': return Formula(2, read(exp[:i]), read(exp[i+1:]))
elif exp[i]=='∨': return Formula(3, read(exp[:i]), read(exp[i+1:]))
elif exp[i]=='→': return Formula(4, read(exp[:i]), read(exp[i+1:]))
return AtomicFormula(exp)
while True:
try:
exp = input("Sequent> ").replace(' ','')
if exp=="exit": sys.exit()
left , right = exp.split('⇒')
seq = Sequent(list(map(read, left.split(','))), (list(map(read, right.split(',')))))
if seq.is_tautology():
print(seq.prooftree())
else:
print("Not Provable")
except EOFError:
sys.exit()
except (AttributeError, ValueError):
print("Error: Invalid Input")