どうも、ここ最近ジムで懸垂のトレーニングを頑張っていますが、一向に身体が上がらない RikiyaOta です。
今年中には上げられるようになりたい。。。
さて、最近趣味で Rust に入門しまして、日々コンパイラーの繰り出す数々の暴力アドバイスに感謝しながら学習をしております。
その中で、再帰的データ構造を定義することに取り組んでみたのですが、思ったより詰まってしまったのと、学びも多かったので個人的に整理してみようと思います。
この記事で伝えること
この記事では、Rust で再帰的データ構造を表す型を定義する方法について、Box<T>を用いた実装例を説明してみたいと思います。
具体例としては、木構造を取り上げます。
また、成功例だけでなく、ありがちな失敗例も取り上げてみたいと思います。
以下の記事で例示したコードはこちらに置きました。
再帰的データ構造とは
再帰的データ構造は、そのデータ構造が自分自身を参照するような構造を持つものです。
よく例として挙げられるのは、やはり木構造でしょう。
あるいは、連結リストなどを思い浮かべる人も多いと思います。
ありがちな失敗例
Rustで再帰的データ構造を定義する際に、Box<T>を使わずに実装しようと考えた時、例えば以下のようなものが思いつくかなと思います。
pub struct InvalidBinaryTree<T> {
value: T,
left: InvalidBinaryTree<T>,
right: InvalidBinaryTree<T>,
}
しかしこちらはコンパイルが通りません。以下のようなエラーが発生します。
error[E0072]: recursive type `InvalidBinaryTree` has infinite size
--> src/binary_tree.rs:21:1
|
21 | pub struct InvalidBinaryTree<T> {
| ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
22 | value: T,
23 | left: InvalidBinaryTree<T>,
| -------------------- recursive without indirection
|
help: insert some indirection (e.g., a `Box`, `Rc`, or `&`) to break the cycle
|
23 | left: Box<InvalidBinaryTree<T>>,
| ++++ +
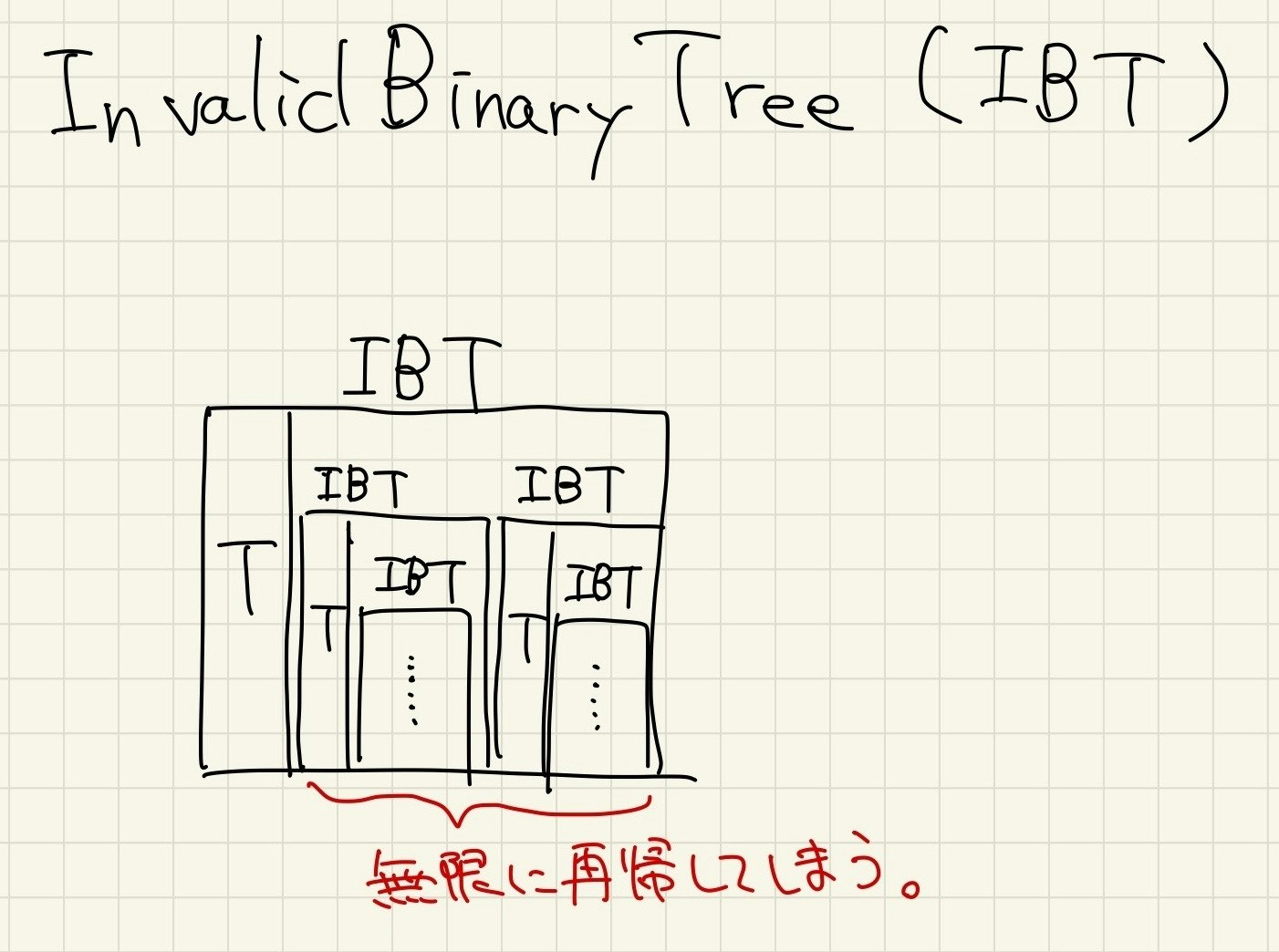
コンパイラーは、このInvalidBinaryTreeの定義を見て、この型の値を格納するのにどれくらいのサイズが必要なのかを知ろうとします。しかし、愚直に再帰させているがために、サイズがどこまでも大きくなってしまい、コンパイルエラーになってしまいます。
また、実は上のInvalidBinaryTreeは、木の終端や、片方の子を持たないようなノードを表現することができていない点でも、不完全な型定義になってしまっています。
『子ノードを持つ』『子ノードを持たない』というように、複数の状態を持つデータ構造を定義するのにはenumが適しています。
そう考えて、今度はenumを使ってこちらも素朴に定義してみると、以下のような形が考えられます。
pub enum InvalidBinaryTree2<T> {
Node {
value: T,
left: InvalidBinaryTree2<T>,
right: InvalidBinaryTree2<T>,
},
Leaf {
value: T,
},
}
こちらもやはり以下のようなコンパイルエラーが発生してしまいます。
以下のようなコンパイルエラーが発生します。
error[E0072]: recursive type `InvalidBinaryTree2` has infinite size
--> src/binary_tree.rs:31:1
|
31 | pub enum InvalidBinaryTree2<T> {
| ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
...
34 | left: InvalidBinaryTree2<T>,
| --------------------- recursive without indirection
|
help: insert some indirection (e.g., a `Box`, `Rc`, or `&`) to break the cycle
|
34 | left: Box<InvalidBinaryTree2<T>>,
| ++++ +
やはり同じく、型が無限のサイズを持ってしまっているようですね。
Box<T>を使うことで解決
この問題を解決するために、Box<T>を使ってデータをヒープに格納することで、再帰的な構造を持つデータを扱うことができます。
Box<T>は、ヒープ上にデータを格納するためのスマート『ポインタ』です。
これによって、再帰的な構造を持つデータを扱うことができます。
それでは実際に動く例を説明したいと思います。
木構造の例
以下に、Rustで二分木を表現する例を示します。
pub enum BinaryTree<T> {
Node {
value: T,
left: Box<BinaryTree<T>>,
right: Box<BinaryTree<T>>,
},
Leaf {
value: T,
},
Empty
}
今度は無事にコンパイルが通ります!
上記の例では、BinaryTreeというenumを定義しています。
それぞれのノードは、値(value)と左右の子ノードへの参照(left, right)を持ちます。子ノードへの参照はBox<BinaryTree<T>>で表現されています。
また、ノードが存在しないことを表現するためにEmptyというバリアントも用意しました。
なぜBox<T>を使うことで問題が解決されるのか
Box<T>は実際の値ではなく、値を指すポインタなので、コンパイラはBox<T>が必要とするメモリサイズを知っています。
ですので、Box<T>を使うことで、再帰的データ構造のサイズが確定することになります。
これは、Box<T>がスタック上にはポインタサイズのメモリ領域しか確保せず、実際のデータはヒープ上に格納されるためです。これによって、再帰的データ構造を持つデータが、スタックオーバーフローを引き起こすことなく扱えるようになります。
また、Box<T>は所有権を持つスマートポインタであるため、リソースの解放も適切に行われるという点でもメリットがあります。
構造体に参照のフィールドを持つと、所有権周りの扱いが結構難しくなると初心者の僕は感じていて、その意味でもBox<T>はとても扱いやすいなぁと今は思っています。
まとめ
この記事では、Rustで再帰的データ構造を表現する方法として、Box<T>を用いた実装方法を紹介しました!
具体例として、木構造を挙げさせていただき、また、Box<T>を使わずに実装しようとすると発生するコンパイルエラーについても触れました。
再帰的データ構造はいろんなところで現れますし、またこれを適切に用いることはプログラムを洗練させることに大きく役立つので、今回学んだ知識をこれから活かしていきたいと思います!
参考
-
こちらのドキュメントでは、Cons List を例に説明がされていました。図を使ってわかりやすく説明がされていました。 ↩