初めに
内容
scikit-learnを用いた機械学習を行います。
データセットはscikit-learnから提供されるデータセットを使用します。
本記事では「Boston house-prices」を取り扱います。
irisデータセットの記事はこちらです。
diabetsデータセットの記事はこちらです。
digitsデータセットの記事はこちらです。
その他のデータセットは別の記事にて更新しようと思います。
対象
主に初心者向けです。が、入門向けではないです。
本記事は友人に向けて作成してますが、
「機械学習したい」と思っている方にも読んでもらえるように書いています。
実装に関しての解説は記載しますが、アルゴリズムなどの解説は(基本的に)しませんのでご理解のほどを。
環境
- Google Colaboratory
- Python 3.6.9
- sklearn 0.22.2
- pandas 1.1.5
- matplotlib 3.2.2
ローカルで環境をそろえるのは難しいので(Dockerやクラウドを使えばできますが)
今回はColaboratoryを用います。
上記のバージョンに合わせるとローカル環境でも実行できます。
以降は実際にpythonを用いながらになるのでColaboratoryの用意をお願いします。
Boston house-prices について
Boston house-prices はボストン市郊外における地域別の住宅価格のデータセットです。
目的変数
まず、目的変数について確認しましょう。
from sklearn.datasets import load_boston
import pandas as pd
boston = load_boston()
target = boston.target
df_target = pd.DataFrame(target, columns=['price'])
df_target.head()
次のような表が生成されます。
今回の目的変数は、住宅価格です。(ゆえにcolumnは'price'です)
irisデータセットと違い「分類(Classification)」ではなく「回帰(Regression)」になることに注意しましょう。
説明変数
次に、説明変数について確認しましょう。
data = boston.data
feature_names = boston.feature_names
df_data = pd.DataFrame(data, columns=feature_names)
df_data.head()
次のような表が生成されます。
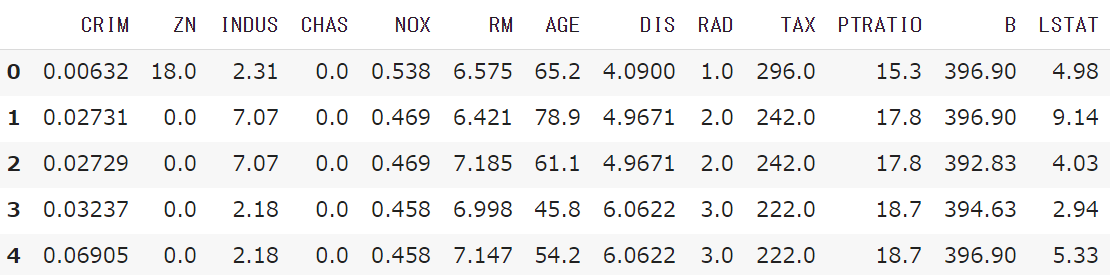
各説明変数は以下のような内容のデータです。
| feature_name | 内容 |
|---|---|
| CRIM | 人口 1 人当たりの犯罪発生数 |
| ZN | 25,000 平方フィート以上の住居区画の占める割合 |
| INDUS | 小売業以外の商業が占める面積の割合 |
| CHAS | チャールズ川によるダミー変数 (1: 川の周辺, 0: それ以外) |
| NOX | NOx の濃度(窒素酸化物の濃度) |
| RM | 住居の平均部屋数 |
| AGE | 1940 年より前に建てられた物件の割合 |
| DIS | 5 つのボストン市の雇用施設からの距離 (重み付け済) |
| RAD | 環状高速道路へのアクセスしやすさ |
| TAX | $10,000 ドルあたりの不動産税率の総計 |
| PTRATIO | 町毎の児童と教師の比率 |
| B | 町毎の黒人 (Bk) の比率を次の式で表したもの。 1000(Bk – 0.63)^2 |
| LSTAT | 給与の低い職業に従事する人口の割合 (%) |
| (scikit-learn に付属しているデータセット/Boston house-prices/各カラムの構成 より) |
機械学習ではこれらの説明変数のうち不要なものを間引く作業が入ります。
データの件数(レコード)はshapeで確認します。
df_data.shape # => (506, 13)
506件あることが確認できます。
相関関係を見る
pandasのscatter_matrixを用いて、すべての目的変数のペアプロットを作成します。
ペアプロットを作成することにより、目的変数の相関関係を見ることができます。
これは、特徴量の選定を行う基準の一つにすることができますね。
import matplotlib.pyplot as plt
pd.plotting.scatter_matrix(pd.concat([df_data, df_target], axis=1), figsize=(20, 20))
plt.show()
concatでdf_dataとdf_targetを結合したものを返します。df_data, df_targetは変更されてませんよ。
plt.show()を行うことで、生成されたインスタンス名(こんなの:<matplotlib.axes._subplots.AxesSubplot object at 0x7fd130b15668>)が表示されなくなります。
次のようなマトリクスが生成されます。(サイズはfigsizeからお好みで変更を)
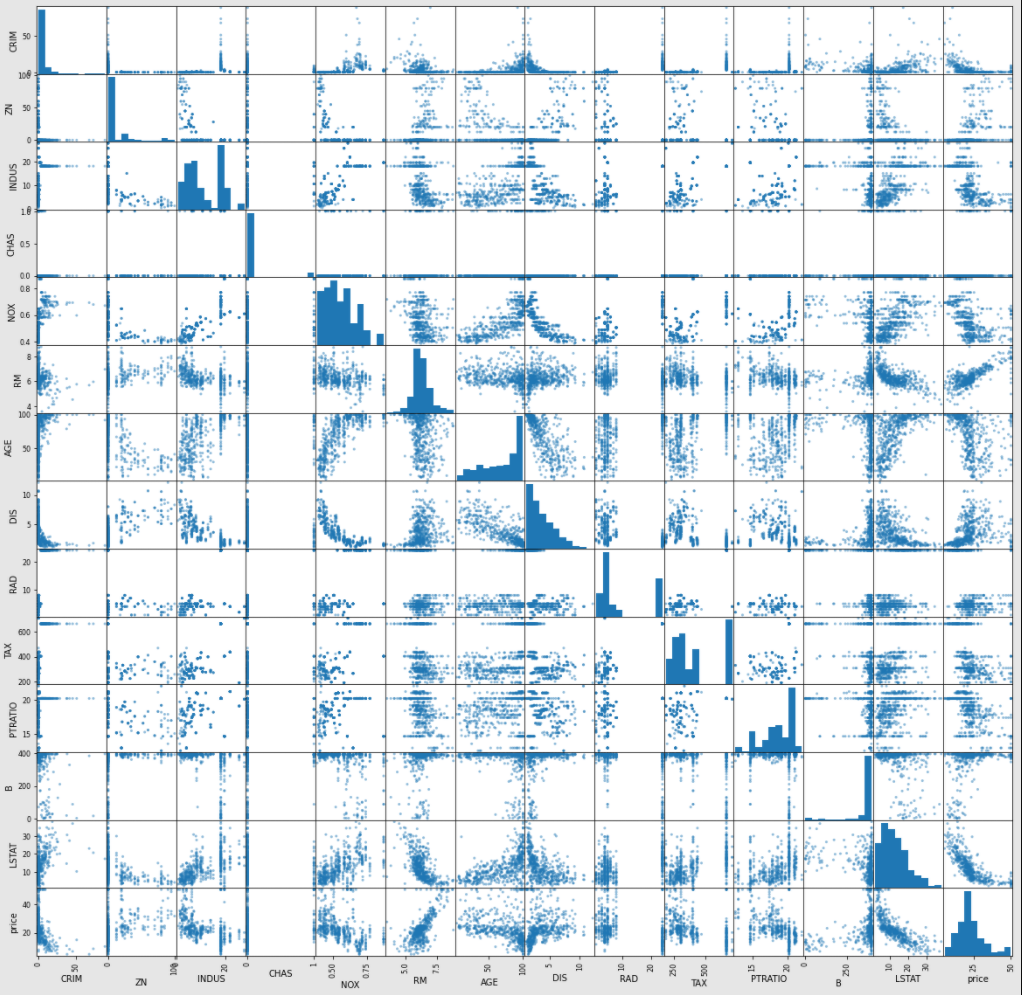
'price'と各説明変数における散布図を見ましょう。(一番下の行)
縦軸に'price'、横軸に説明変数が来ます。
例えば'price'と'CRIM'の散布図に着目してみましょう。(一番下左)
この散布図からは'CRIM'が低いとき'price'が高い傾向にあることがわかります。
(犯罪発生率が低いとき、価格が高い)
'price'と'RM'の散布図に着目すると、'RM'が大きいとき'price'が高いことがわかるでしょう。
(部屋数が多いとき、価格が高い)
これらのように、散布図から目的変数に対して影響度の高い(低い)説明変数を読み取れるようになります。
機械学習しよう
前処理
必須の前処理として、データに欠損値があるかどうかを確認します。
目的変数に欠損値が含まれていればtrueが返ってきます。
df_data.isnull().any()
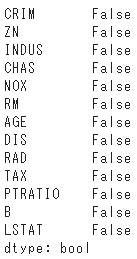
今回はすべてfalseなので欠損値はありませんね。
(データによっては欠損値が特定の値で埋められてたりするので、無いとは断言できないのですが...)
データを学習データと検証データに分割しましょう。
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(df_data, df_target, test_size=0.2, random_state=100)
print('x_train :', x_train.shape) # => x_train : (404, 13)
print('y_train :', y_train.shape) # => y_train : (404, 1)
print('x_test :', x_test.shape) # => x_test : (102, 13)
print('y_test :', y_test.shape) # => y_test : (102, 1)
random_stateを変更すれば学習結果も変わってきます。
今回、特徴量の選定は行いません。
興味があれば調べて、行ってみましょう。
学習
今回のモデルはlinear_modelのlassoを使用します。
他のモデルを使用したいのであれば公式リファレンスやほかの方のQiita記事をご覧ください。
from sklearn.linear_model import Lasso
model = Lasso()
model.fit(x_train, y_train)
推論
モデルの評価には$R^2$を使用します。
$R^2$の場合、出力が1に値悪なるほど良いモデルとされます。
評価方法は他にも、MSEやMAEなど多数存在しますので、適切な評価方法を選択できるようにしましょう。
from sklearn.metrics import r2_score
pred = model.predict(x_test)
r2_score(y_test, pred) # => 0.6776294232065305
人の目から見て、$R^2$のみではどれくらいの精度かが分かりにくいので、予測値と本当の値を可視化してみましょう。
import numpy as np
x = np.arange(y_test.shape[0])
plt.title('Comparison of measured and predicted values')
plt.ylabel('price')
plt.plot(x, y_test, label='y_test')
plt.plot(x, pred, label='pred')
plt.legend()
plt.show()
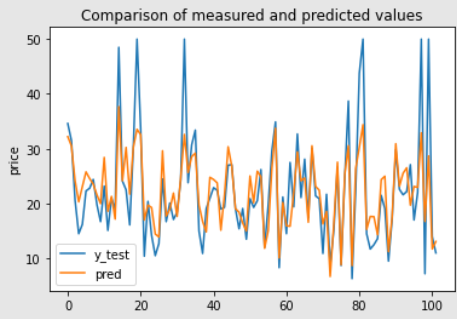
縦軸が価格で、横軸がデータ102件分(train_test_splitの分割数により変化する)を表します・
凡例の通り青線がy_test、オレンジ線がpredです。
高額な値に対しての予測ができていないため$R^2$の値が低いようですね。
今回の高額な値は、全体的に見ると外れ値に相当するので、予測できなくても問題ないかと思います。
それ以外の値では、比較的近い値が出力できているようなので、評価指数のみでモデルの精度を判断するのは早計かもしれないですね。
最後に
普段分類問題ばかり取り組んでいるため、新鮮な感じでした。
私自身、回帰における評価指数の適切な選び方がわかっていないようなので、まとめてみたいと思います。