これは個人的なメモです。間違っているかもしれないので注意してください
ご指摘等あればよろしくお願いします
(1)では、リアルタイムを想定してボリュームレンダリング方程式の解き方を考える
(2)では、具体的なシーンを想定してGLSLで実装する
前提
- 光が粒子に当たると、散乱(scattering)と吸収(absorption)が起こる
散乱:光の方向が変わる
吸収:光が粒子に吸収され、別の形のエネルギーになる
これら二つの現象をまとめて、減衰(extinction)と呼ぶ
- 粒子の大きさにより散乱のしかたが変わる
粒子の大きさ<光の波長:レイリー散乱(Rayleigh scattering)
粒子の大きさ>光の波長:ミー散乱(Mie scattering)
- 散乱について、入射した光がどの方向へどの程度出るかを表す関数を位相関数(phase function)と呼ぶ
位相関数は粒子の屈折率、大きさ、光の波長に依存する
前述のレイリー散乱、ミー散乱はそれぞれ異なる位相関数を持つ
(はっきりと異なっているわけでは無く、依存する変数について滑らかにつながってる)
-
粒子が詰まった空間を関与媒質(participating media)と呼ぶ
-
関与媒質中の散乱は複数回発生すると考えられる。これを多重散乱(multiple scattering)と呼ぶ
多重散乱は複雑すぎてリアルタイムでは扱うのが難しいので、単一散乱(single scattering)だけ考える
単一散乱:光が粒子によって一回だけ散乱する
ボリュームレンダリング方程式について
定義は以下の通り
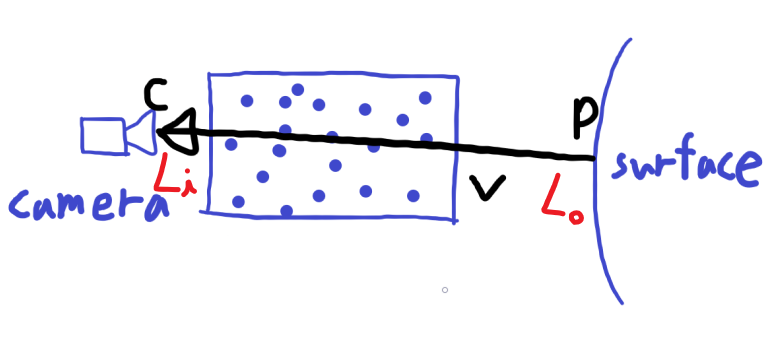
- カメラの位置:$c$
- サーフェスの点:$p$
- $d:=|c-p|$
- $v:=\frac{c-p}{d}$
- $x_t:=c-vt \qquad (0 \leq t \leq d)$
- 吸収係数(absorption coefficient):$\sigma_a$
- 散乱係数(scattering coefficient):$\sigma_s$
- 減衰係数(extinction coefficient?):$\sigma_e = \sigma_a + \sigma_s$
- これらの係数は位置に依存する
求めたいのは、$p$から$c$までの経路上でカメラに向かう光の総量$L_i(c,-v)$(放射輝度)
(この経路以外にも$c$に向かう光はあると思うかもしれないが、今は$-v$しか見ていないので無視する)
$L_i(c,-v)$に加わる光を一つ一つ考えていき、最期にそれらを足し合わせる
減衰後のサーフェスpからの光
まず考えるのは、サーフェス$p$からの光$L_o(p,v)$
関与媒質が無い場合$L_i(c,-v)=L_o(p,v)$となるはずだが、関与媒質があるので減衰が起こる
$p$から$c$までに減衰が発生し、その結果残る光の割合を透過率(transmittance)と呼ぶ
透過率は以下の式で表される
$T_r(p,c)=e^{-\tau}$
$\tau=\int_{p}^{c}\sigma_e(x)|dx|$
これはランベルト・ベールの法則(Lambert-Beer law)と呼ばれる
サーフェスからの光によって$c$に入射する放射輝度は以下のように表される
$L_{\mathrm{surf}}(c,v) = T_r(p,c)L_o(p,v)$
光源からの光の入散乱(in-scattering)
光源からの光が散乱し、カメラに入射することが考えられる
これを入散乱(in-scattering)と呼ぶ
入散乱で入射する放射輝度の、位置$x_t$での微小変化は以下のように表される
$dL(x_t,v) = \sigma_s(x_t) \int_{S^2}f_p(x_t,w,v)L_i(x_t,w) dw \ dt$
点$x$に入射する全ての方向の光を考え、そのうち$v$方向に散乱する光の総量を求めている
位相関数$f_p(x,w,v)$は、位置$x$において$w$方向で入射した光が$v$方向に散乱する割合を表す
これは正規化されており、全球積分すると1になる
$\int_{S^2}f_p(x,w,v) dw=1$
入散乱によって$c$に入射する放射輝度は以下のように表される
$L_{is}(c,v) = \int_{0}^{d} T_r(x_t,c) \left[\sigma_s(x_t)\int_{S^2}f_p(x_t,w,v)L_i(x_t,w) dw \right]dt$
$x_t$によって$x_t(0) = c$から$x_t(d) = p$までの経路について積分している
$T_r(x_t,c)$がかかっているのは、こちらの光も前述と同じように減衰するからである
媒質の発光(emission)
媒質自体が発光(emission)している場合がある(炎など)
この場合、位置$x_t$での微小変化は以下のように表される
$dL(x_t,v) = L_e^V(x_t,v) dt$
$L_e^V(x_t,v)$は体積放射率関数(volume emittance function)と呼ばれ、単位長当たりの放射輝度を表す
発光によって$c$に入射する放射輝度は以下のように表される
$L_{e}(c,v) = \int_{0}^{d} T_r(x_t,c) L_e^V(x_t,v)dt$
足し合わせ
これらをまとめると、以下のような式が得られる
$L_i(c,-v) = L_{\mathrm{surf}}(c,v) + L_{is}(c,v) + L_{e}(c,v)$
$= T_r(p,c)L_o(p,v) + \int_{0}^{d} T_r(x_t,c) \left[L_e^V(x_t,v) + \sigma_s(x_t)\int_{S^2}f_p(x_t,w,v)L_i(x_t,w) dw \right]dt$
この式をボリュームレンダリング方程式(volume rendering equation)と呼ぶ
この右辺を解けば、カメラに入射する放射輝度が求まる
リアルタイムでの実装を考える
$L_{\mathrm{surf}}(c,v) , L_{is}(c,v) , L_{e}(c,v)$の求め方を一つづつ考える
L_surfを求める
式は
$L_{\mathrm{surf}}(c,v)=T_r(p,c)L_o(p,v)$
$L_o(p,v)$は既知なので、$T_r(p,c)$を求めれば良い
$T_r(p,c)=e^{-\tau}$
$\tau=\int_{p}^{c}\sigma_e(x)|dx| =\int_{c}^{p}\sigma_e(x)|dx|$
この積分は解析的に解けないので、区分求積法を用いて数値積分をしてみる(台形でもシンプソンの公式でもいいと思う)
直線の経路積分なので、固定長レイマーチングをする
// 減衰係数
float extinction_coefficient(vec3 x);
// L_surfを求める
// 既知: p,c,L_o(p,v)
const int n=30;
float d=length(c-p);
vec3 v=(c-p)/d;
float step=d/float(n);
float tau=0.0;
// 固定長レイマーチング
for(int i=0;i<n;i++)
{
float t=float(i)*step;
vec3 x_t=c-v*t;
// 区分求積法(長方形)
tau+=extinction_coefficient(x_t)*step;
// 特筆すべき点として、この時点で tau(x_t,c)
// つまり Tr(x_t,c)が求まっている
}
// T_r(p,c)
float Tr=exp(-tau);
vec3 L_surf=Tr*L_o;
$L_{\mathrm{surf}}(c,v)=T_r(p,c)L_o(p,v)$が求まった
L_isを求める
式は
$L_{is}(c,v) = \int_{0}^{d} T_r(x_t,c) \left[\sigma_s(x_t)\int_{S^2}f_p(x_t,w,v)L_i(x_t,w) dw \right]dt$
一部を抜き出して定義し直す
$L_{scat}(x_t,v) := \sigma_s(x_t)\int_{S^2}f_p(x_t,w,v)L_i(x_t,w) dw$
$L_{is}(c,v) = \int_{0}^{d} T_r(x_t,c) L_{scat}(x_t,v)dt$
まずはこの$L_{scat}(x_t,v)$を求める
$L_{scat}(x_t,v)$内部の全球積分はグローバルイルミネーション(大域照明,global illumination,GI)を考慮した式である
ローカルイルミネーション(局所照明,local illumination)だけ考慮する場合は全球積分が不要になる
簡単のためポイントライトのみを考え、以下の様に定義する
- $i$番目のポイントライトからx_tへの放射輝度$L_{light_i}(x_t)$
- $i$番目のポイントライトの位置$p_{light_i}$
- $l_i := \frac{p_{light_i} - x_t}{| p_{light_i} - x_t |}$
- 可視性関数(visibility function) $f_v$ 解説は後述
すると、$L_{scat}(x_t,v)$は以下のように表される
$L_{scat}(x_t,v) = \pi \sigma_s(x_t) \sum_{i=1}^n f_p(x_t,l_i,v)f_v(x_t,p_{light_i})L_{light_i}(x_t)$
$f_v(x_t,p_{light_i})$は光源$p_{light_i}$から$x_t$に達する光の割合を表す関数で、以下のように表される
$f_v(x_t,p_{light_i}) := S(x_i,p_{light_i})T_r(x_i,p_{light_i})$
透過率$T_r$に加え不透明な物体による遮蔽を考慮するため、その影を$S(x_i,p_{light_i})$として乗算している
以上で$L_{scat}(x_t,v)$が求まった
実装は以下の通り
// 散乱係数
float scattering_coefficient(vec3 x);
// 位相関数
float phase_function(vec3 x,vec3 w,vec3 v);
// yからxまでの、不透明な物体による影を求める(割愛)
float shadow(vec3 x,vec3 y);
// i番目の光源の位置
vec3 light_pos[i];
// i番目の光源からxへの放射輝度
vec3 light_color(x,i);
// yからxまでの透過率を求める
float transmittance(vec3 x,vec3 y)
{
const int n=15;
float d=length(y-x);
vec3 v=(y-x)/d;
float step=d/float(n);
float tau=0.0;
// 固定長レイマーチング
for(int i=0;i<n;i++)
{
float t=float(i)*step;
vec3 x_t=y-v*t;
// 区分求積法(長方形)
tau+=extinction_coefficient(x_t)*step;
}
return exp(-tau);
}
// pからxに達する光の割合
float visibility(vec3 x,vec3 p)
{
return shadow(x,p)*transmittance(x,p);
}
// L_scat(x,v)を求める
float L_scat(vec3 x,vec3 v)
{
const int light_num=3;
float lsum=0.0;
for(int i=0;i<light_num;i++)
{
vec3 l=normalize(light_pos[i]-x);
lsum+=phase_function(x,l,v)*visibility(x,light_pos[i])*light_color(x,i);
}
return lsum;
}
では$L_{is}(c,v)$を求める
$L_{is}(c,v) = \int_{0}^{d} T_r(x_t,c) L_{scat}(x_t,v)dt$
こちらの積分も$T_r$と同じように数値積分をするが、計算量を減らすため$L_{\mathrm{surf}}(c,v)$の計算中で求まっている$T_r(x_t,c)$を流用する
$L_{\mathrm{surf}}(c,v)$の実装に追記し、以下のようになった
// L_surf,L_isを求める
// 既知: p,c,L_o(p,v)
const int n=30;
float d=length(c-p);
vec3 v=(c-p)/d;
float step=d/float(n);
float tau=0.0;
vec3 L_is=vec3(0.0);
// 固定長レイマーチング
for(int i=0;i<n;i++)
{
float t=float(i)*step;
vec3 x_t=c-v*t;
// 区分求積法(長方形)
tau+=extinction_coefficient(x_t)*step;
// 特筆すべき点として、この時点で tau(x_t,c)
// つまり Tr(x_t,c)が求まっている
float Tr=exp(-tau);
L_is+=Tr*L_scat(x_t,v)*step;
}
// T_r(p,c)
float Tr=exp(-tau);
vec3 L_surf=Tr*L_o;
$L_{is}(c,v)$が求まった
L_eを求める
式は
$L_{e}(c,v) = \int_{0}^{d} T_r(x_t,c) L_e^V(x_t,v)dt$
これも$L_{is}(c,v)$の実装と同じように$L_{\mathrm{surf}}(c,v)$中の$T_r(x_t,c)$を流用できるので、$L_{\mathrm{surf}}(c,v)$の実装に追記する
// 体積放射率関数(volume emittance function)
vec3 volume_emittance(vec3 x,vec3 v);
// L_surf,L_is,L_eを求める
// 既知: p,c,L_o(p,v)
const int n=30;
float d=length(c-p);
vec3 v=(c-p)/d;
float step=d/float(n);
float tau=0.0;
vec3 L_is=vec3(0.0),L_e=vec3(0.0);
// 固定長レイマーチング
for(int i=0;i<n;i++)
{
float t=float(i)*step;
vec3 x_t=c-v*t;
// 区分求積法(長方形)
tau+=extinction_coefficient(x_t)*step;
// 特筆すべき点として、この時点で tau(x_t,c)
// つまり Tr(x_t,c)が求まっている
float Tr=exp(-tau);
L_is+=Tr*L_scat(x_t,v)*step;
L_e+=Tr*volume_emittance(x_t,v)*step;
}
// T_r(p,c)
float Tr=exp(-tau);
vec3 L_surf=Tr*L_o;
$L_{e}(c,v)$が求まった
足し合わせてL_i(c,-v)を求める
$L_i(c,-v) = L_{\mathrm{surf}}(c,v) + L_{is}(c,v) + L_{e}(c,v)$
より、前述の三つの項を足し合わせれば良い
// ボリュームレンダリング方程式を解く
// p: サーフェスの点
// c: カメラの位置
// L_o: サーフェスからの放射輝度 L_o(p,v)
vec3 volume_rendering(vec3 p,vec3 c,vec3 L_o)
{
const int n=30;
float d=length(c-p);
vec3 v=(c-p)/d;
float step=d/float(n);
float tau=0.0;
// L_a:=L_is+L_e
vec3 L_a=vec3(0.0);
// 固定長レイマーチング
for(int i=0;i<n;i++)
{
float t=float(i)*step;
vec3 x_t=c-v*t;
// 区分求積法(長方形)
tau+=extinction_coefficient(x_t)*step;
// 特筆すべき点として、この時点で tau(x_t,c)
// つまり Tr(x_t,c)が求まっている
float Tr=exp(-tau);
L_a+=Tr*(L_scat(x_t,v)+volume_emittance(x_t,v))*step;
}
// T_r(p,c)
float Tr=exp(-tau);
vec3 L_surf=Tr*L_o;
return L_surf+L_a;
}
$L_{is}$と$L_e$を足し合わせて$L_a$としているのは、その方が計算精度が良いからである
これで$L_i(c,-v)$が求まった
まとめ
(2)では今回実装していない部分も含め、具体的なシーンを想定してGLSLで実装します