はじめに
この記事を読んでくださった方へ
つぶやきGLSLをやりましょう!
もうしている方へ
テクニック集をください!
切に願っております…
テクニック
つぶやきGLSLのテクニックをコード短縮とそれ以外に分けてまとめていきます(随時更新)
また、全てのテクニックはTwiglのgeekest(300es)を想定しています
コード短縮
floatの短縮
float a=0.1;
↓
float a=.1;
1文字の短縮です
int型からのキャスト
vec3 a=vec3(1.,2.,3.);
↓
vec3 a=vec3(1,2,3);
int1つあたり1文字の短縮です
不必要な代入の削除
vec3 a,b,c;
a=vec3(1);
b=floor(a);
c=mod(b,2.)-1.;
↓
vec3 c=mod(floor(vec3(1)),2.)-1.;
当然と言えば当然ですが、連鎖的に消える事もあり強力です
vec型へのキャスト
float s=1.;
o=vec4(s);
↓
float s=1.;
o+=s;
かなり多用します
for文の短縮
vec3 a=vec3(1,2,3),b,c;
for(float i=0.;i<99.;i++)
{
b+=a*i;
c=b-vec3(1);
}
↓
vec3 a=vec3(1,2,3),b,c;
for(float i;i++<99.;)b+=a*i,c=b-vec3(1);
(for文の中身は変えていません)
- floatの初期値は0.0なので初期化不要
- i++をiの評価と同時に行って短縮
- ,で式を1文にして中カッコを削除
ということをやっています
距離の二乗
vec3 P;
float a=dot(P,P);
で求まります
floorの代替
ceilでどうにかなる時があります
代入の返り値を用いる
float a=5.,b,c;
b=sin(a);
c=b;
↓
float a=5.,b,c;
c=b=sin(a);
宣言時に計算する
vec3 a=vec3(1,2,3),b=vec3(4,3,2);
↓
vec3 a=vec3(1,2,3),b=a.zyx+1.;
たまに使えます
defineの変な使い方
#define F(P) dot(vec3(1,2,3),P)
vec3 P=vec3(3,2,1);
float a=F(P.xxx),b=F(P.yyy),c=F(P.zzz);
↓
#define F(S) dot(vec3(1,2,3),P.S)
vec3 P=vec3(3,2,1);
float a=F(xxx),b=F(yyy),c=F(zzz);
まれに使います
他にも算術演算子を引数にしたりと、defineは柔軟性が高いです
乗算、除算の反転
例えばa*10.0はa/.1にすることができます
定義済み変数の利用
oはvec4(0)として、sは0.0として使えます
また、floatの変数が必要だが定義をしたくない場合、o.a等を変数として使うことができます
↓例
for(;o.a++<99.;)何かの処理;
あまり多用する場合、floatを宣言した方が短くなることもあるため、万能ではありません
次元を上げるときにキャストを利用する
float s;
vec2 a=vec2(s)
↓
float s;
vec2 a=o.aa+s;
たまにこれを使い忘れます
レイの定義
vec3 R=vec3((FC.xy*2.-r)/r.y,1);
正規化していないので、このままではアーティファクトが出ます
これを回避する方法として、SDFに0.5等を掛ける、という手法があります
これは、SDFが正確でなくても下限であればレイマーチングできる、という性質を使った方法です
それ以外
座標変換
(Pをレイの先端として)
- 複製
mod(P,n)-n/2. - 折り返し
abs(P.x) - ねじる
P.xy*=rotate2D(P.y)
値の離散化
離散化したいときはfloor(p*N)/Nとします(場合に応じてceilでも可)
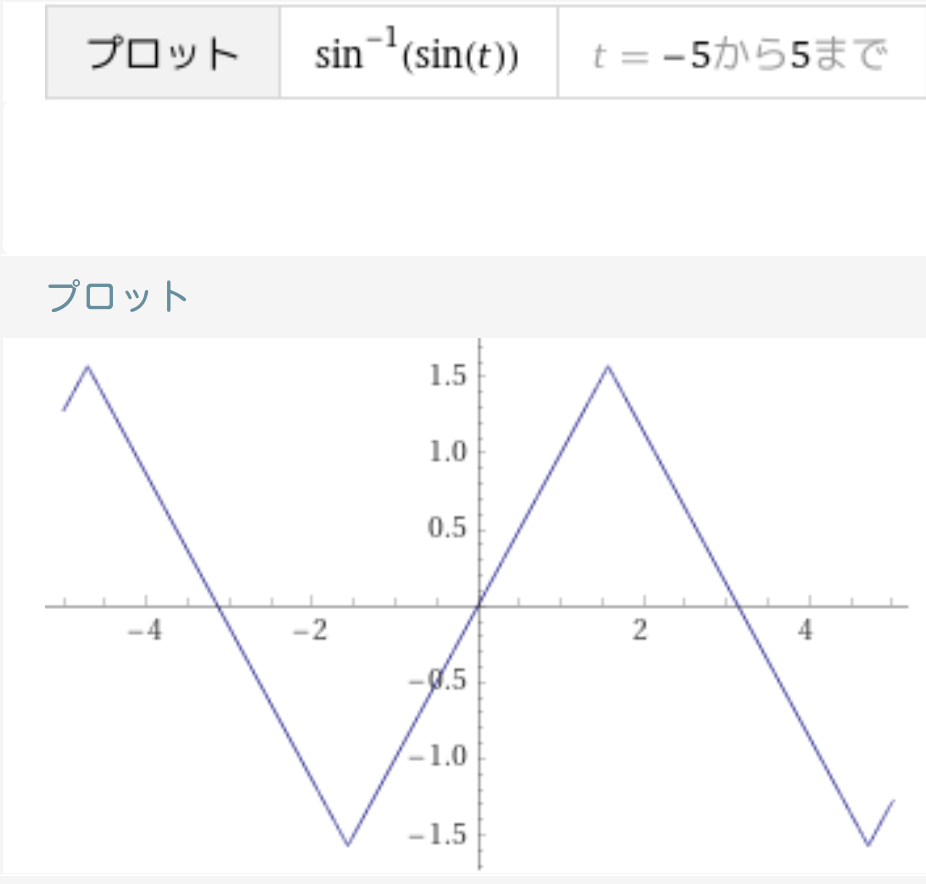
三角波
レイマーチング
vec3 R=vec3((FC.xy*2.-r)/r.y,1),O=vec3(0,0,0),P;
float i,l,d=1.;
for(;i++<99.&&d>.01;)
{
P=R*l+O;
d=length(P)-.5;
l+=.5*d;
}
o+=12./i;
短縮する前の私のテンプレはこんな感じです
レイマーチングの説明は割愛
DDX法によるボクセルの描画
vec3 Y=vec3((FC.xy*2.-r)/r.y,.5),I=sign(Y),O=vec3(0,0,f/4.),D=I/Y,M=ceil(O),S=(I*(M-O+.5)+.5)*D,T,K;
for(;O.r++<99.&&O.b>0.;)
{
K=vec3(lessThanEqual(S,min(S.yzx,S.zxy)));
S+=K*D;
M+=K*I;
O.b=length(mod(M,20.)-10.)-7.;
}
o+=12./O.r;
これが短縮前のコードです
DDXアルゴリズムについてはこちらを参照
fwidthを用いた擬似的な法線、輪郭検出
レイの先端をP,ステップ数をiとすると
fwidth(P*20.)などで法線が、fwidth(i*.1)などで輪郭が取れます
理由としては、fwidthがabs(dFdx(p))+abs(dFdy(p))の為です。
あまり理解していませんが、レイマーチングで法線を取る時に勾配を用いるのと似た感じだと思います
固定長でレイマーチング
vec3 Y=vec3((FC.xy*2.-r)/r.y,1),G=vec3(5,0,t),P;
float i,d=1.;
for(;i++<1e2&&d>0.;)
{
P=Y*i/10.+G;
d=snoise3D(P)+.5;
}
o+=10./i;
ボリュームレンダリングの要領で固定長でレイを進め、衝突したら打ち切ります
通常よりコードを短縮できますが、のっぺりとした絵になります
Diffuse 法線不使用
Xorさんのテクニックです
// P:衝突点,L:ライトの方向,e:EPS
float light=max(SDF(P+L*e)-SDF(P),.0)/e
Diffuse 法線使用
vec3 N=normalize(cross(dFdy(P),dFdx(P)));
float light=dot(N,L);
uniformの活用
- 's==0'
- 'FC.zw==(0.5,1)'