あらすじ
教授「進化計算の基本となる基本アルゴリズムはこんな感じだぞ」
我「へーすごーい」
教授「今日の講義内容だけで、進化計算はできるぞ」
我「ふーん…」
や っ て み た
概要
求める関数
f(x)=-cos(x)*cos(x/20) (-25.5≦x≦25.5) (0.1刻み)
個体
要素数9の配列
0番:正負を決める(0:正、1:負)
1~8番:8桁の2進数を構成する(i番目:2^(8-i)の倍数)
よって、個体が持つ値の範囲は-255~255
遺伝アルゴリズムのサイクルは以下の通り(授業の受け売り)
0→1→2→3→4→1→2→…
0. 初期集団
解を特定しにくい(今回の場合はしやすいが)ため、解となる個体を乱数で設定する
個体の乱数の要素:0 or 1
1. 適応度の計算
関数の最大値を求めるため、適応度はf(x)の値とする
t:個体の値とすると、適応度は以下の通りとなる
f(x/10)
2. 親の選択
今回は、エリート保存戦略(適応度が高い順に個体を選ぶ)を用いて個体群から親を2人選んだ。
3. 交叉
今回は、一様交叉を行い子の個体を作成した。
一様交叉
個体と同じ形マスクを用意する。
各番号のマスクの要素の値に応じて対応する番号の遺伝を以下の通りに行う。
- マスクの要素0:親1→子1、親2→子2
- マスクの要素1:親1→子2、親2→子1
4. 突然変異
5%の確率で、交叉後の子の配列のランダムに選択した番地の要素を変更した。(0→1、1→0)
(確率の基準は標準偏差で2σ≒95%だからとかいう安直な理由の元設定)
環境
python 3.5.1
numpy 1.15.2
実践
ソースコードは以下の通り(長いので後でGitHubに載せます)
import numpy as np
import math
import random
import matplotlib.pyplot as plt
GENE_NUM = 10 #個体数
def f(x):
return -np.cos(x)*np.cos(x/20)
def init(genes):
for i in range(GENE_NUM):
for j in range(9):
genes[i][j] = random.randint(0,1)
# 初期集団の形成
def x(gene):
result=0
for i in range(8):
result += pow(2, i)*gene[8-i]
if(gene[0]==1):
result = result*-1
return float(result/10)
# 交叉・突然変異
def evolve(gene1, gene2, mnum):
result = np.zeros((2,9))
# 交叉
for i in range(9):
r=random.randint(0,1)
if(r==1):
result[0][i]=gene2[i]
result[1][i]=gene1[i]
else:
result[0][i]=gene1[i]
result[1][i]=gene2[i]
#突然変異
r = random.random()
if(r<0.05):
rnum = random.randint(0,8)
if(result[0][rnum]==0):
result[0][rnum]=1
else:
result[0][rnum]=0
if(0.95<r):
rnum = random.randint(0,8)
if(result[0][rnum]==0):
result[1][rnum]=1
else:
result[1][rnum]=0
return result
def main():
genes = np.zeros((GENE_NUM,9))
genenum = 0
init(genes)
#進化サイクル
while(genenum<20):
#出力
print(genenum)
print(genes)
plt.figure()
rx = np.arange(-25.5, 25.5, 0.01)
ry = f(rx)
plt.plot(rx,ry)
for i in range(GENE_NUM):
rx = x(genes[i])
ry = f(rx)
plt.scatter(rx,ry)
plt.savefig("./result/"+str(genenum)+".png")
firstrate=-100
secondrate=-100
first=-1
second=-1
#選択
for i in range(GENE_NUM):
rate=f(x(genes[i]))
if(rate>firstrate):
secondrate=firstrate
second=first
firstrate=rate
first=i
elif(rate>secondrate):
secondrate=rate
second=i
tmp1=genes[first]
tmp2=genes[second]
genes[GENE_NUM-1]=tmp1
genes[GENE_NUM-2]=tmp2
for i in range(int(GENE_NUM/2)-1):
result=evolve(genes[GENE_NUM-1], genes[GENE_NUM-2],i)
genes[i*2]=result[0]
genes[i*2+1]=result[1]
genenum+=1
if __name__ == '__main__':
main()
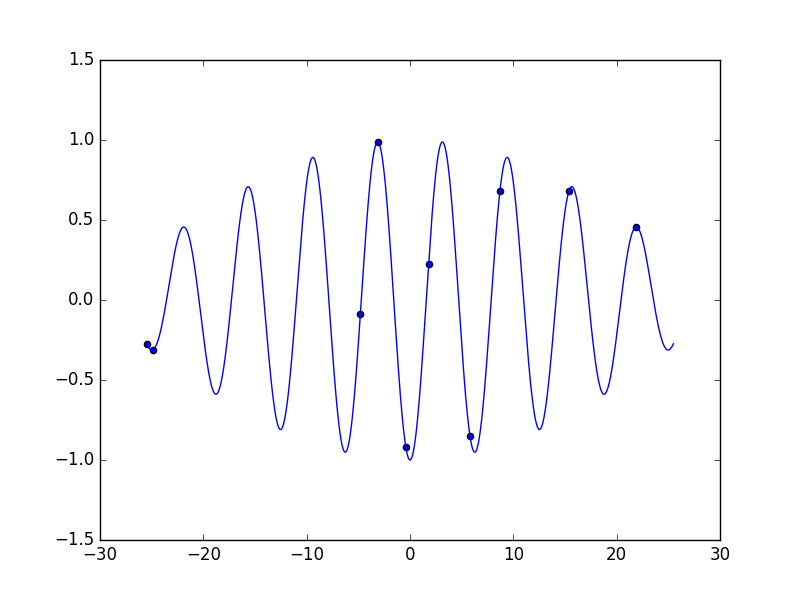
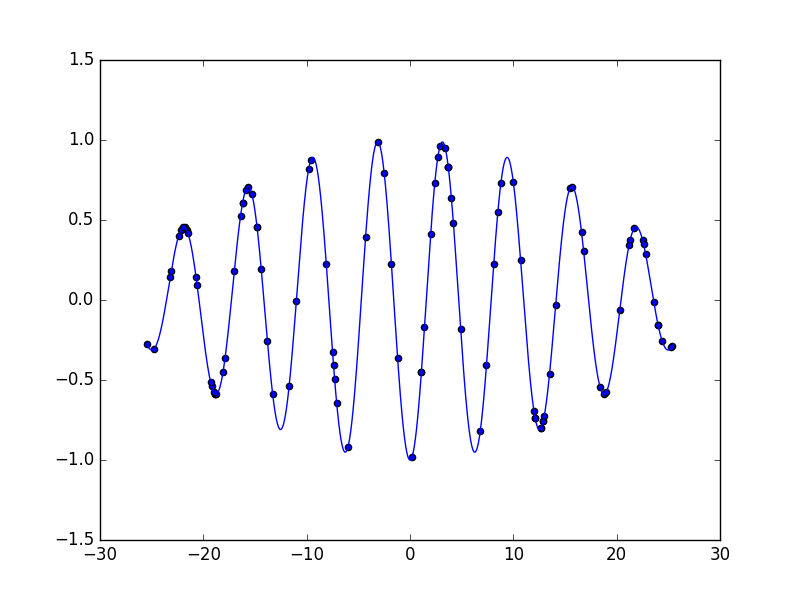
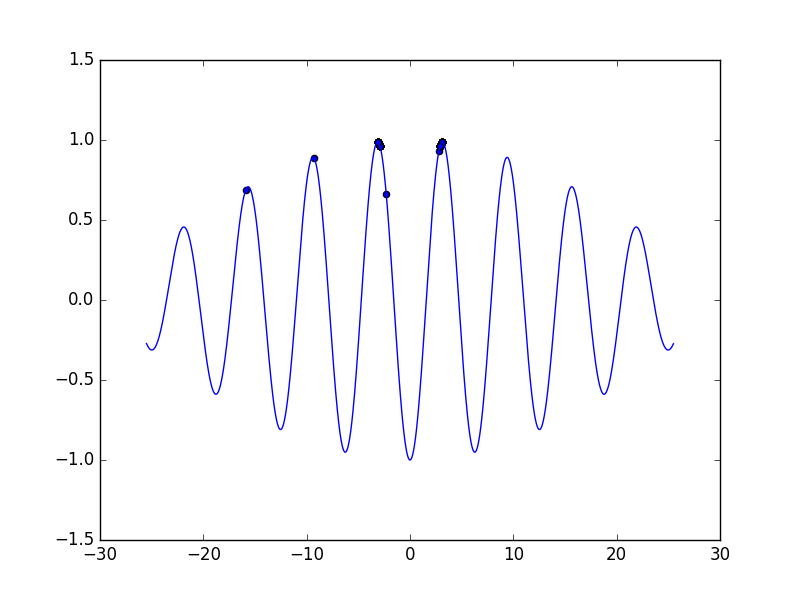
結果はこちら(グラフの0に近い2つの凸の頂点が最大値)
以降は1世代目と同じ位置に個体が固まっていた。
なんとびっくり、1回の進化だけで、最大値を導き出したのだ!
進化計算すごい!
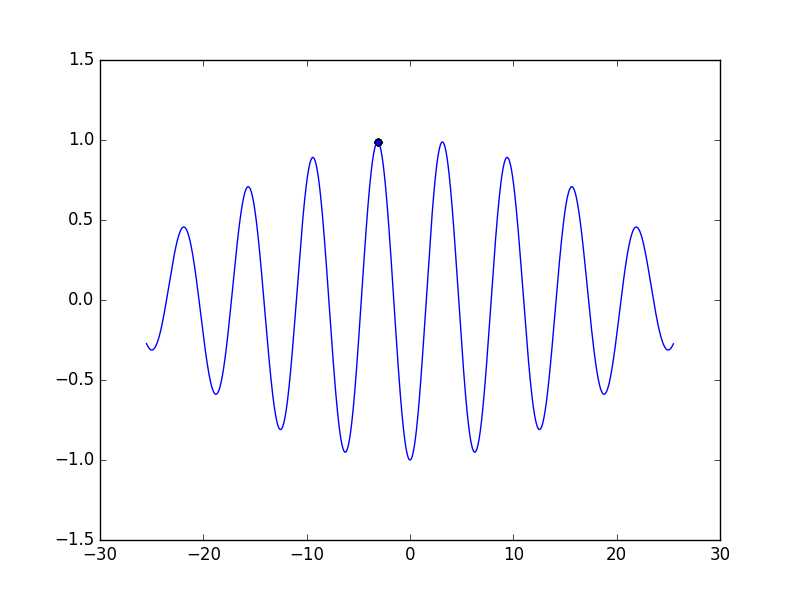
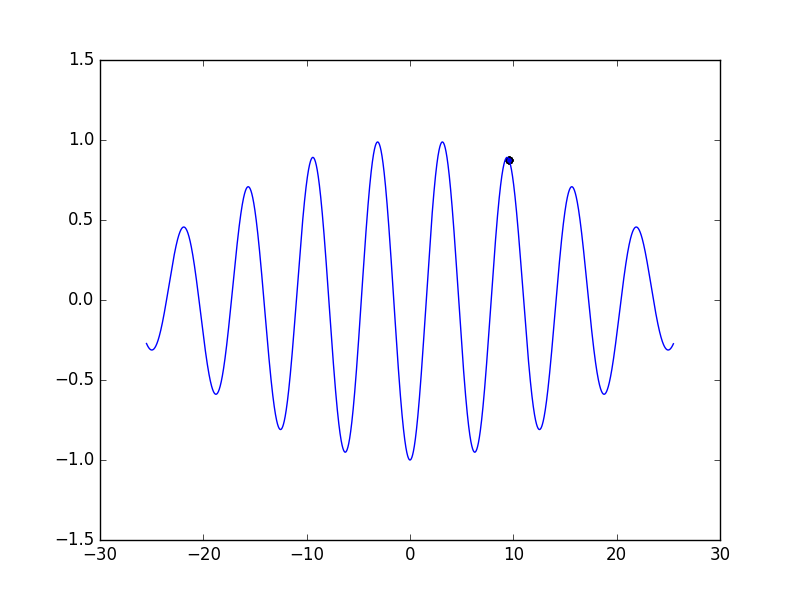
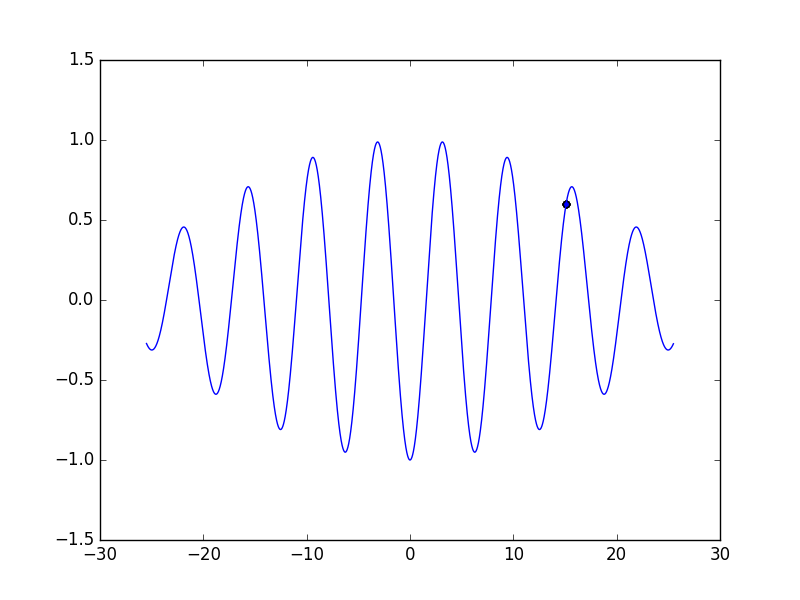
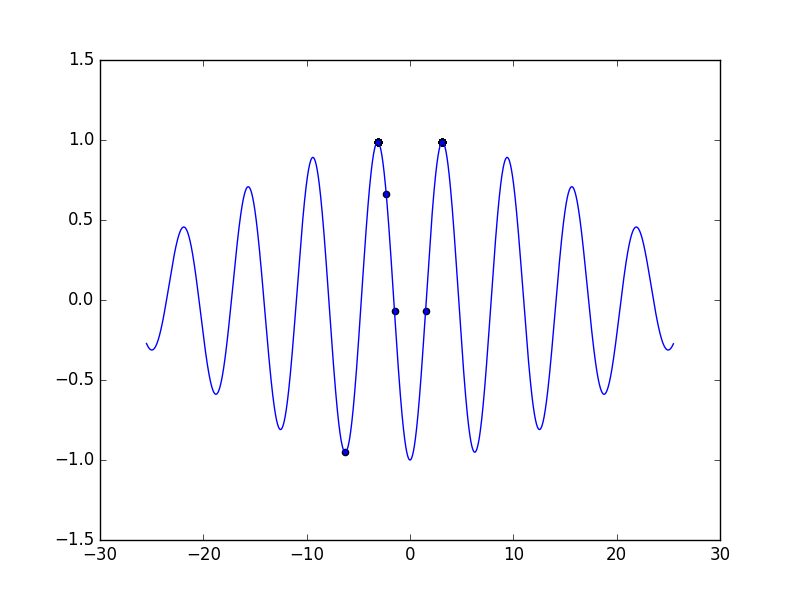
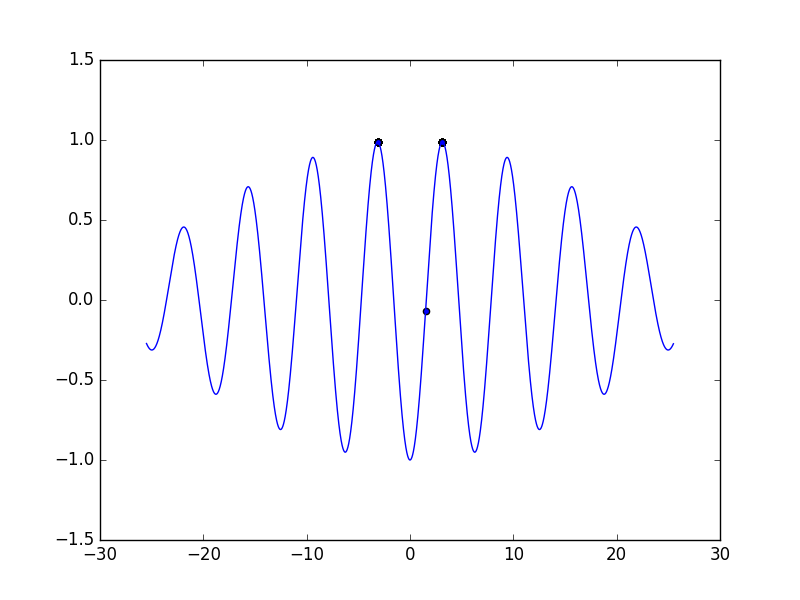
…なんてことはありえないので、追加で数回実行してみると
ご覧の通り、見事に間違った結果を出した。
その後細かい修正等を重ねてみたがなかなか上手くいかず、講義の日がやって来たのでどうすればいいか聞いて見ることにした。
相談
我「なかなか上手くいかないんです…」
教授「個体数足りんからちゃう?」
我「なるほど」
個体数10→100
修正結果
なかなか良い感じになった
まとめ
軽くしか触れてないけど、進化計算楽しいなって思った(雑)
画像認識の研究室行こうかなと思ったけど、進化計算もいいかもしれない。
次は物理運動の最適化とかやってみたい。