今回のネタ
本記事の投稿日3月14日は円周率の日であり、この日に円周率関連の記事を投稿するのが一つのネタとなっているようです。
7年前にもこういった記事がありました。
GeForceで円周率小数点以下8000兆桁目の計算を達成
karrelsらは複数のGPU(GTX 690×4枚、GTX 680×2枚、GTX 570×24枚)を使い26日ほどかけて円周率2進法表記の8000兆桁目(16進2000兆桁目と同じ)を計算し、3月14日に公表しました。今回はこの彼らがやった計算結果が本当に正しかったのか1からコードを組み検算してみたいと思います。
(念のため補足するとここでいう"2000"兆桁、"8000"兆桁の数字は10進法(=9+1進法)での2000,8000です。)
検証内容
元の情報をたどると
http://www.karrels.org/pi/index.html
ここに小数点第2000000000000000桁目から653728f1ですと書いてあるので、この数値に合致するかを検証します。
円周率の16進法表記最初の数十桁
円周率は普通3.14で覚えていますが、今回求めようとしているのはあくまで16進法での円周率です。なんとなく感覚をつかむために円周率16進法表記の最初の数十桁を載せます。
π = 3.243f6a8885a308d313198a2e03707344a4093822299f31d008・・・
またこれ以降明らかに文章として出てくる数字は10進法表記としています。円周率の計算結果のみ16進法で表記しています。
円周率の公式
円周率を求める公式はいくつもありますが大きく分けて、小数点第1桁目から全て求めるものと、小数点第〇〇桁目から求めるものがあります。詳しくは円周率jpに書いてありますが、小数点第〇〇桁目を求めてみた系はだいたいこのBellardの公式かBBPの公式が使われています。というかBellardの一強です。2020/3現在このサイトによるとBellardの式を使って高橋大介の10京桁が世界最大の桁数のようです。
Bellardの式
π=\frac{1}{64} \sum_{k=0}^{∞} \frac{(−1)^k}{1024^k} (-\frac{32}{4k+1}-\frac{1}{4k+3}+\frac{256}{10k+1}-\frac{64}{10k+3}-\frac{4}{10k+5}-\frac{4}{10k+7}+\frac{1}{10k+9})
小数点第2000兆桁を求めたいならk=0からk=800000000000000(800兆)+αくらいまでやることになります。
3行でCLBellardの紹介
下にいろいろ実装が書いてありますが、このBellardの公式で円周率を計算するソフトを作りました。OpenCLで動くのでCLBellardです。
データのありかはコチラ(github)です。
結果
それでは早速結果です。
A :starting at 210^15
B :starting at 210^15-5
A run: 653728f1d92ef9802795ab97da55a474f01a254eb8b11447
B run: 28fec653728f1d92ef9802795ab97da55844e0400db36fce
^^^^^^^^^^^^^^^^^^^^^^^^^^^^
ということで
653728f1d92ef9802795ab97da55
まで正確ということでよさそうです!
あってました。わーい
一応ちゃんと計算した証拠として、Bellardの式の各項別(全部で7つ)の小数点以下の結果を示します。
S1=\frac{1}{64} \sum_{k=0}^{∞} \frac{(−1)^k}{1024^k} (-\frac{32}{4k+1})
S2=\frac{1}{64} \sum_{k=0}^{∞} \frac{(−1)^k}{1024^k} (-\frac{1}{4k+3})
S3=\frac{1}{64} \sum_{k=0}^{∞} \frac{(−1)^k}{1024^k} (\frac{256}{10k+1})
S4=\frac{1}{64} \sum_{k=0}^{∞} \frac{(−1)^k}{1024^k} (-\frac{64}{10k+3})
S5=\frac{1}{64} \sum_{k=0}^{∞} \frac{(−1)^k}{1024^k} (-\frac{4}{10k+5})
S6=\frac{1}{64} \sum_{k=0}^{∞} \frac{(−1)^k}{1024^k} (-\frac{4}{10k+7})
S7=\frac{1}{64} \sum_{k=0}^{∞} \frac{(−1)^k}{1024^k} (\frac{1}{10k+9})
とし$16^{2000000000000000}S1$ , $16^{2000000000000000}S2$ ・・・の小数点以下の数値はそれぞれ
3df9af6ea22018861a072069d53
b09b3ceb478ac509be5950c9405
1efed32be2ff3de2c804d5784a0
04e138cac621be99e4e8bb68db1
7f5acc1c3b4d2843f87463ecb3e
b533a7eaaffb015df95144d2575
1e33bc9a5b1af5d1b08200c4946
でした。なお下位桁はすこしずれている可能性があります。
計算時間
今回の結果を得るまでに、複数のGPUをおよそ10日間くらいぶん回す必要がありました。しかし10日と長い時間計算し続けていると計算エラーも怖いです。なので計算が終わったら、もう一度同じ計算をやりなおすということをして正誤判定をしました。つまり単純に2倍時間がかかります。計算結果は一括で計算して出力するのではなく、一部だけ計算してファイルに書き出すことで複数GPUで分担することも可能となり、どこでエラーが起こっているかもわかりやすくなります。具体的にはBellard式の7項(7STEP)×5821Batchに分割して計算しました。
ここでは1週目の計算時間を記載しています。
| GPU名 | 計算時間(h) | 仕事量(Batch数) | 1Batchあたりの計算時間(ms) |
|---|---|---|---|
| RTX2080 1台目 | 238.6 | 13423 | 64004 |
| RTX2080 2台目 | 210.8 | 11513 | 65927 |
| TITAN V | 242.9 | 12711 | 68787 |
| GTX 1080 | 172.3 | 1925 | 322205 |
| RX 480 | 167.4 | 940 | 641012 |
| HD 7970 | 45.34 | 235 | 694511 |
エラー発生回数
次に計算エラーの内訳です。ここでも1週目のエラーのみを載せています。
| GPU名 | エラー回数 | 内訳 |
|---|---|---|
| RTX2080 1台目 | 0 | |
| RTX2080 2台目 | 0 | |
| TITAN V | 0 | |
| GTX 1080 | 16 | OCしたら0を出力1回。OCしたらINFを出力15回。 |
| RX 480 | 2 | ディスプレイドライバ停止が原因で0を出力1回。謎の1bit反転1回。 |
| HD 7970 | 7 | ディスプレイドライバ停止が原因で0を出力2回+適当な値を出力5回。 |
このように計算エラーは1つを除いて、GPU側の原因というよりはレジストリ設定不足と下手なオーバークロックをしていた人間側のせいでした。
ディスプレイドライバ停止とは、OSがWindowsの時に画面描画を担当するGPUが計算タスクでいっぱいになり画面の更新が2秒以上とまった場合にOSがドライバーを強制終了してしまうことで、これは
https://support.borndigital.co.jp/hc/ja/articles/360000574634
このようにレジストリをいじることで回避できます。
オーバークロックに伴うエラーについては、GTX 1080をMSI Afterburnerでだいたい100-200Mhzくらいオーバークロックしていました。FAN 100%にして常用しているときは温度も75度前後で見た目エラーを吐いてるように見えなかったですが、後で確認すると2時間に1回くらいの微妙なペースでエラーを吐いていることが分かりました。それが分かってからはオーバークロックなしでFAN speedだけ100%にして計算させたところ、エラーが止まりました。
人間側が原因のエラーの内訳はこんな感じでした。ということなので上の表だけ見て計算時間あたりのエラー回数とかは参考にしないでください。
宇宙線によるbit反転らしきエラー
RX480で起こった1bit反転については2週目の計算結果を待つまでわかりませんでした。1STEP目の2246Batch目で1回だけ起こっていました。
1週目 RX 480で計算 不正解
1cc4c98275c5a6b07aa292・・・
^^
2週目 RTX 2080Tiで計算 正解
1cc4ca0275c5a6b07aa292・・・
^^
こんな感じに、左から6,7桁目がずれていました。差はa0-98=02です。プログラム上ではメモリに計算結果を加算していくような形にしていたため最終的には2桁にわたってずれていますが、差をとってみると2という数字がでてきました。ずれとしては1bit分。ひょっとしてこれが噂の宇宙線によるbit反転!?
もちろん2週目のほうが間違っている可能性も考慮しこのBatchだけ3週目を計算し2週目が合っていることを確認しています。
この計算エラーを見つける前までは円周率の2000兆桁目が
自分の結果
65372871
karrelsらの結果
653728f1
とでていたのでどっちが正しいのか分からずもんもんとしていました。おそらくこんなことが起こるだろうと思っていたので2回同じ計算をしてみて良かったです。
実装
まずGPUで計算するのが前提だったため並列処理をどう書くかが重要でした。
次に、上のBellard式をただ愚直に実装するとdouble型でも精度が足りなさ過ぎて円周率小数点以下10桁くらいまでしか求められません。なので以下の要素を取り入れる必要がありました。
約10億桁まで求める:除数が32bit整数までのべき乗余
約100京桁まで求める:除数が64bit整数までのべき乗余
精度をあげる:擬似四倍精度(double-double演算)
もっと精度をあげる:擬似四倍精度2つから192bit固定小数点数を作る
高速化:モンゴメリ乗算
並列化
今回行う計算の大部分は以下の式の計算でk=0,1,2,3....と代入して計算し、合計していくというものです。
S1=\frac{1}{64} \sum_{k=0}^{∞} \frac{(−1)^k}{1024^k} (-\frac{32}{4k+1})
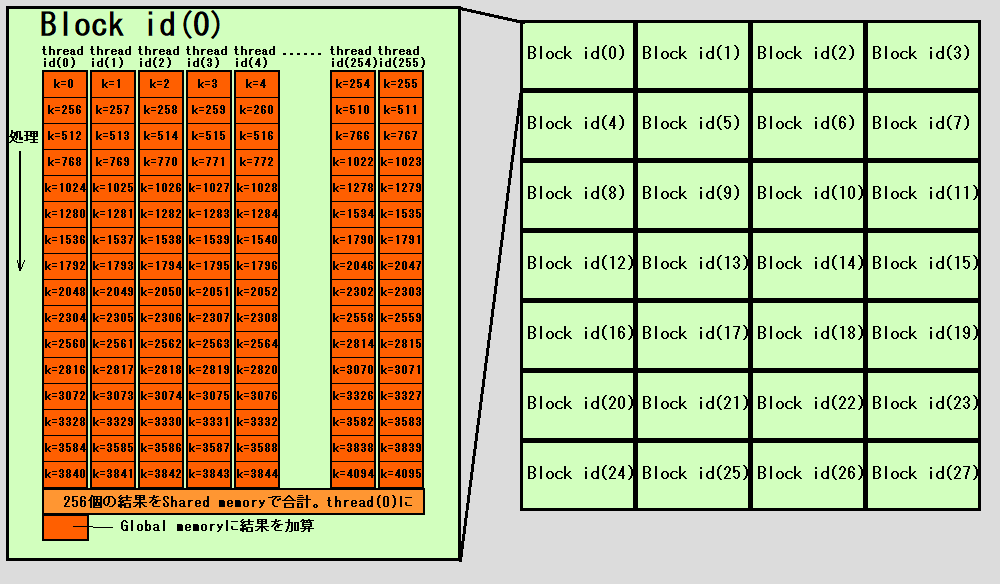
そこでk=0,k=1...をそれぞれ別スレッドで計算し並列化してやります。
図のように1つのthread内でも複数のkのパターンを計算し、合計していきます。足す順番は関係ないのでこれで良いです。block内で最後にshared memory等つかって合計値を求めます。そのあとは各blockの出力を合計するだけです。ここはお好みですが、global memoryに値を足しこむときAtomic演算を使っても良いし、blockの数だけglobal memoryを確保しておきblockごとの結果を全部保持し最後に合計計算するとしても良いです。
ここでいうthread、blockとはCUDA用語ですが、OpenCLで言うところのwork_item、work_groupになります。
この計算は計算量に対しメモリアクセス量がとても少なく、さらに分散計算に向いているので非常に並列化しやすいです。なにもこの図の通りにやらなくてもよいと思いますし、GPUの演算器数が増えれば増える分だけ速くなると思われます。もちろん複数GPUでやるのも可能です(別途合計プログラムが必要)。
べき剰余
次に各thread内で行う計算について順次考えていきます。結論から言うとBellard、BBPはべき乗余を計算する問題になっていきます。
円周率小数点第n+1桁目を求めたいとすると、計算する必要があるのは$16^{n}π$の小数部分です。重要なのでもう一度言いますが求めたいのはあくまで小数部分のみです。マイナスの場合は1.0を足してプラスの小数にしてよいとします。
16^{n}π=16^{n}\frac{1}{64} \sum_{k=0}^{∞} \frac{(−1)^k}{1024^k} (-\frac{32}{4k+1}-\frac{1}{4k+3}+\frac{256}{10k+1}-\frac{64}{10k+3}-\frac{4}{10k+5}-\frac{4}{10k+7}+\frac{1}{10k+9})
最初の項だけ抽出して考えます。
16^{n}S1=16^{n}\frac{1}{64} \sum_{k=0}^{∞} \frac{(−1)^k}{1024^k} (-\frac{32}{4k+1})
これをごにょごにょやるとこうなります。
=-32\sum_{k=0}^{∞}(−1)^k(\frac{1024^{\frac{2n-3}{5}-k}}{4k+1})
$\frac{2n-3}{5}$をdとおき
=-32\sum_{k=0}^{∞}(−1)^k(\frac{1024^{d-k}}{4k+1})
都合よくdは整数でd-k>=0としておきます。ここで$(\frac{1024^{d-k}}{4k+1})$の小数部分のみが求まれば良いということが言えます。
(この小数だけ分かればΣで足していって繰り上がりで1以上になっても整数部分は無視し、最後32をかけた後も整数部分は無視すると$16^{n}S1$の小数部分と一致しますよね。)
a=$1024^{d-k}$ , b=$4k+1$ として
a/bの小数部分 = a%b /b
と言えるのでa%bの部分が "xのy乗をmで割ったあまり" という形になっておりここにべき剰余が使えることが分かります。べき剰余の具体的なアルゴリズムについてはここでは省略します。
と、ここまでの解説は例によって円周率jpにも書いてあるので(むしろBBP式で解説されているのでわかりやすい)こっちもご覧下さい。
d-k<0の場合はまだ考えていないですがこの場合$1024^{-1}$とかでてきてべき剰余は使えません。ただ実際の計算ではd-k>=0となるパターンがほとんどです。2000兆桁目の計算ではd=800兆くらいになりd-k>=0が800兆パターンあるのに対し、d-k<0となるパターンはせいぜい20程度です。なのでそこは計算効率とか気にせず愚直に計算すればよいです。
除数が32bit整数までのべき乗余
ここではべき剰余をOpenCLに実装していくことを考えます。OpenCLでは組み込み型で64bit整数のulong型があるのでこれを使えば一発です。
ulong ExpMod32(ulong a,ulong n,const ulong modC){
ulong ans=1;
for(int i=0;i<64;i++){
if (n%2==1){
ans=(ans*a)%modC;
}
a=a*a%modC;
n/=2;
if (n==0)break;
}
return ans;
}
除数が64bit整数までのべき乗余
ところが除数が32bitを超えると途中必要なサイズがulongでもおさまらなくなります。除数が32bitを超えはじめるのは円周率11億桁くらいからです。
64bit64bit%64bitという剰余計算自体ができないので、これをOpenCLでできるように考えます。OpenCLにはmul_hi命令といって、64bit64bit整数の乗算結果のうち上位桁64bitを返す命令があります。これをなんとか使えないか・・・と悩みに悩んだ結果超汚いコードがかけましたのでこれを使います。
//超汚い剰余未証明
//1:only modC >= (1<<32)
//2:only a*b<modC*modC
//return a*b mod modC
ulong ABmodC64(const ulong a,const ulong b,const ulong modC)
{
ulong xc=(((ulong)1<<(ulong)63)%modC)*(ulong)2;
xc-=(xc>=modC)*modC;
ulong anslo=a*b; // (64bit)
ulong anshi=mul_hi(a,b); // (64bit)
ulong c1=modC>>(ulong)32; // (32bit)
ulong c2=modC%((ulong)1<<(ulong)32); // ull c2=c&0x00000000FFFFFFFF;
// In actuality, c1 c2 are not calculate per for loops
ulong s=anshi/c1; // (64bit)/(32bit)=(32bit)
if (s>c1) s=c1;
anshi-=s*c1; // (64bit)-(32bit)*(32bit)=(32bit) there is no underflow possibility
ulong scfrg=s*c2;// (32bit)*(32bit)=(64bit)
anshi-=scfrg>>(ulong)32; //(32bit)-((64bit)>>32)=(32bit or underflow)
scfrg<<=(ulong)32; //((64bit)%(32bit))<<32=(64bit) 32-63bit usd
//anshi-=(anslo<scfrg); // (64bit)<(64bit) (32bit or underflow)-(1bit)=(32bit or underflow)
if (anslo<scfrg)anshi--;
anslo-=scfrg; // (64bit)-(64bit)=(64bit or underflow).This underflow is already resolved.
ulong anslo_tmp=anslo;
if (anshi>((ulong)1<<(ulong)63))
{ // faster than anshi&8000000000000000
anshi+=c1; // (32bit or underflow)+(32bit)=(32bit)
anslo+=c2<<(ulong)32; //(64bit)+(32bit)*(1bit)*(32bit)=(64bit or overflow)
}
if (anslo<anslo_tmp)anshi++;
s=( anshi*((ulong)1<<(ulong)32) + (anslo>>(ulong)32) ) /c1; // ( ((32bit)<<32) + ((64bit)>>32) )/(32bit)=(32bit)
scfrg=s*c1; // (32bit)*(32bit)=(64bit)
anshi-=scfrg>>(ulong)32; // (32bit)-((64bit)>>32)=(32bit) there is no underflow possibility.
scfrg<<=(ulong)32; // ( ((64bit)%(32bit))<<32 )=(64bit) 32-63bit use
if (anslo<scfrg)anshi--;
anslo-=scfrg; // (64bit)-(64bit)=(64bit or underflow).This underflow is already resolved.
scfrg=s*c2; // (32bit)*(32bit)=(64bit)
if (anslo<scfrg)anshi--;
anslo-=scfrg; // (64bit)-(64bit)=(64bit or underflow) This underflow is already resolved.
anshi-=mul_hi(s,c2);
if (anshi>((ulong)1<<(ulong)63))
{
anslo=(ulong)0-anslo;
}
ulong resans=anslo%modC;
if (anshi>((ulong)1<<(ulong)63))
{
if (anslo!=(ulong)0)anshi++;
resans=(modC*(ulong)2-resans-((ulong)0-anshi)*xc);
if (resans>=modC)resans-=modC;
if (resans>=modC)resans-=modC;
}
return resans;
}
考え方としては桁を2つに分割して除算みたいな感じです。もうちょっとなんとかならないかと思って後日書き直したのでやっぱりこっちを使います。
//逆数乗算みたいなやつ
//この事前計算が必要
void hoge()
{
ulong log2modC=64-clz(modC);
double dr1=(double)((ulong)1<<log2modC);
dr1=dr1*dr1;
ulong rmodC=(ulong)(dr1/(double)modC);
}
ulong ABmodC64(const ulong a,const ulong b,const ulong modC,const ulong rmodC,const ulong log2modC)
{
ulong blo=a*b;
ulong bhi=mul_hi(a,b);
ulong b1=(bhi<<((ulong)64-log2modC))|(blo>>log2modC);
ulong b2lo=b1*rmodC;
ulong b2hi=mul_hi(b1,rmodC);
ulong b2=(b2hi<<((ulong)64-log2modC))|(b2lo>>log2modC);
ulong b2alo=b2*modC;
ulong b2ahi=mul_hi(b2,modC);
bhi-=b2ahi;
if (blo<b2alo)bhi-=1;
blo-=b2alo;
if (bhi==(ulong)18446744073709551615){
bhi=0;
blo+=modC;
}
//この時点でbは最大4modC-1
if (bhi>0){
if (blo<modC)bhi-=1;
blo-=modC;
}
//この時点でbの最大は4modC-1
if (blo>=modC){
blo-=modC;
}
//この時点でbの最大は3modC-1
if (blo>=modC){
blo-=modC;
}
//この時点でbの最大は2modC-1
if (blo>=modC){
blo-=modC;
}
return blo;
}
本来rmodCを求めるのに128bit/64bitの計算が必要になってきますが、ちょっとズルをしてdouble型でやっています。それだと53bit分くらいしか信頼できないですが、後に出てくるdouble-double演算を使えば完全に解決します。
なおモンゴメリ乗算で書いていく際にも128bit%64bitの計算が最初にどうしてもいるので、このコード作っておく意味はあります。
さて、これでさっきのようにべき剰余を書くとこうなります。
ulong ExpMod64(ulong a,ulong n,const ulong modC){
ulong ans=1;
for(int i=0;i<64;i++){
if (n%(ulong)2==(ulong)1){
ans=ABmodC64(ans,a,modC);
}
a=ABmodC64(a,a,modC);
n/=(ulong)2;
if (n==(ulong)0)break;
}
return ans;
}
いろいろ組んだあとにすごく参考になりそうなサイトに出会いました。モンゴメリ乗算や逆数乗算のことなどが書いてあります。
除算・剰余算の高速化
擬似四倍精度で精度up
べき剰余を使って分子を求めたあとは、分母で割って小数部分だけを足していくのでした。この加算部分はdouble型などの浮動小数点数を使うのが実装上は簡単です。ただ何億、何兆回も足していくとさすがに数値誤差が気になります。
例ですがdouble型を使ってBellard式で1000000桁目を計算したら以下の数値が出てきたとします。
小数点第1000000桁以降
26c65e520c94a80000000000000000000000
このうちどの位の桁まで信頼できるか、ということを考えます。
確認する方法として1000005桁以降の数値も計算してみてどこまで合致するか目視で確認する、という方法が考えられます。
小数点第1000000桁以降
26c65e520c94a80000000000000000000000
e52cb44890d7880000000000000000000000
^ ここまで合ってる!
これで26c65e52まで正確に求められているっぽい感じがします。でも偶然数値が似てしまった可能性は本当にないんでしょうか。本当は有効桁数が3,4桁くらいで、偶然にも下位桁が一致していただけで、26c64e52が正解だったら悲惨です。
これが何兆桁となって有効桁数が1桁にも満たなくなったらやばいのでは?と気になり一度double型の精度保証付きを実装してみました。
10兆桁目を試してみたら
min 0df5184de6a3a
max 114ace9235bc8
これはmix~maxまでの間に正解があることが保証されています。このように有効桁数が1桁も満たないことが分かりました!!
正解は0f9ff371d1であり、ちょうどminとmaxの中間くらいの値になりますがさすがにもうdouble型の精度は信用できないです!
ということで擬似四倍精度を使います。
double2 twosum(const double2 a)
{
double x = (a.x + a.y);
double tmp= (x - a.x);
double y = (a.x - (x - tmp)) + (a.y - tmp);
return (double2){x,y};
}
double2 dsplit(const double a)
{
double tmp = (a * 134217729.0);
double x = (tmp - (tmp - a));
double y = (a - x);
return (double2){x,y};
}
double2 twoproduct(const double2 a)
{
double x = a.x * a.y;
double2 ca = dsplit(a.x);
double2 cb = dsplit(a.y);
double y = (((ca.x * cb.x - x) + ca.y * cb.x) + ca.x * cb.y) + ca.y * cb.y;
return (double2){x,y};
}
double2 addcab(const double2 a,const double2 b)
{
double2 tmp={a.x,b.x};
double2 cz = twosum(tmp);
cz.y = cz.y + a.y + b.y;
return twosum(cz);
}
double2 subcab(const double2 a,const double2 b)
{
double2 tmp={a.x,-b.x};
double2 cz = twosum(tmp);
cz.y = cz.y + a.y - b.y;
return twosum(cz);
}
double2 ddmulcab(const double2 a,const double2 b)
{
double2 tmp={a.x,b.x};
double2 cz = twoproduct(tmp);
cz.y = cz.y + a.x * b.y + a.y * b.x + a.y * b.y;
return twosum(cz);
}
double2 dnmulcab(const double2 a,const double b)
{
double2 tmp={a.x,b};
double2 cz = twoproduct(tmp);
cz.y = cz.y + a.y * b;
return twosum(cz);
}
double2 nnmulcab(const double a,const double b)
{
double2 tmp={a,b};
double2 cz = twoproduct(tmp);
return cz;
}
double2 dd_div(const double2 x,const double2 y)
{
double z1 = x.x / y.x;
double2 tmp={-z1,y.x};
double2 cz = twoproduct(tmp);
double z2 = ((((cz.x + x.x) - z1 * y.y) + x.y) + cz.y) / y.x;
return twosum((double2){z1,z2});
}
double2 dn_div(const double2 x,const double y)
{
double z1 = x.x / y;
double2 tmp={-z1,y};
double2 cz = twoproduct(tmp);
double z2 = (((cz.x + x.x) + x.y) + cz.y) / y;
return twosum((double2){z1,z2});
}
double2 nd_div(const double x,const double2 y)
{
double z1 = x / y.x;
double2 tmp={-z1,y.x};
double2 cz = twoproduct(tmp);
double z2 = (((cz.x + x) - z1 * y.y) + cz.y) / y.x;
return twosum((double2){z1,z2});
}
double2 nn_div(const double x,const double y)
{
double z1 = x / y;
double2 tmp={-z1,y};
double2 cz = twoproduct(tmp);
double z2 = ((cz.x + x) + cz.y) / y;
return twosum((double2){z1,z2});
}
参考にしたのはここ
4倍精度演算ライブラリ
あとDD演算だけでなくなんとQD演算まで移植した方が
https://github.com/KoukiTanaka/OpenCLQD
GPUは基本的にdouble型の計算がえらい遅いのでなるべく使いたくはないですが、この擬似四倍精度を使ってもまだべき剰余の整数計算が7-8割の計算時間を占めていたので恐れすぎる必要はなさそうです。
この擬似四倍精度を導入することで10兆桁目の計算をしても余裕で最初の15-6桁が合致するようになりました。(精度保証付きでやってないのでわからないですがそれでも12,3桁くらい合致すると思われます。)
擬似四倍精度2つから192bit固定小数点数を作る
ここからは読み飛ばしても良いです。もう擬似四倍精度の精度があれば十分なのですが、もう少し欲張ってしまいました。頑張って作ったので書いたってだけであって理解してもらえるとは思っていません。
考え方としては、64bit整数型を3つつなげて192bit分を固定小数点数と見立てて計算できないかというところから始まっています。OpenCLは最大ulong型=64bit整数までですが繰り上がり処理を適切にすれば2つ3つつなげて128bit、192bit整数も擬似的に作れます。小数の情報をこの192bitの整数型にいれて計算すれば、加減算の操作後も小数のみの結果だけが残り都合が良いです。浮動小数点数の時にやってた小数部分の切り出しという操作が加減算時にいらなくなるということです。
次に考えなくてはいけないのが、64bit/64bitの割り算をどうやって192bit正確に計算するかです。何を言っているかというと
$(1024^{d-k}$ $mod$ $(4k+1))$ / $(4k+1)$
これはΣの中身ですが、プログラムでは毎ループkをインクリメントしながらこれを計算しています。この分母、分子は64bit整数で保持されています。(分子は先ほどのべき剰余で求まっている)。この割り算の結果が今度は192bit分必要、ということを言ってます。
192bitの情報が得られたら先ほどの192bit固定小数にいれて計算を進めていくという方針です。ちなみに擬似四倍精度では106bit程度の情報しか得られません。
自分はしばらく上記の式だけで192bitを得るしかないと思い込んでいましたが、よく考えると以下の操作をすればよいことに気づきました。
$(1024^{d-k}$ $mod$ $(4k+1))$ / $(4k+1)$ の除算を擬似四倍精度で計算(1)
$(1024^{d-k}$ $mod$ $(4k+1)$ $×2^{96}$ $mod$ $(4k+1) )$ / $(4k+1)$ の除算を擬似四倍精度で計算(2)
(2)の計算で求めているものは(1)の結果に$2^{96}$をかけて小数部分を取り出してきたものと同じです。ここでは精度の問題があるので割り算をする前に$2^{96}$をかけて分母で剰余するところまで整数で計算している、という具合です。
計算結果を小数点以下から2進法で表示すると例えばこうなっていると考えられます。
(1)の計算結果 ...は省略の意味
11001.....11011010101000010011001010011110
^ ^ ^
0bit目 96bit目 105bit目まで正確
(2)の計算結果
101010000101010101111110.....0100111001101
^ ^ ^
0bit目 9bit目 105bit目まで正確
|~~~~~~~~|この範囲は正確な数字でオーバーラップしているところ
擬似四倍精度の除算を使っているので(1)で計算した結果は0~105bit目まで正確な数値です。(2)の計算は(1)で計算したところに少しオーバーラップさせています。ほぼ同じ値になっていると思われるのでそれを検知して、後ろの(2)の105bit目までをつなげれば1本の201bitが完成します。下位桁をカットすれば192bitになります。
ここで「ほぼ同じ」と言ったのは、(1)結果が最近接丸めになって繰り上がっていることを考慮してです。運が悪いとこうなります。
(1)の計算結果
10110.....11000100000000000000000000000000
^ ^ ^
0bit目 96bit目 105bit目
(2)の計算結果
111111111111111111111111.....1111111111111
^ ^
0bit目 9bit目
(1)が丸めで繰り上がっています。うまい具合に繰り上がりを戻して(2)の結果をつなげる必要があります。もちろん繰り下がりのパターンもあると思うので同じように考えます。
これを考慮し実装するとこうなります。
void dd2_to_ulong3(double2 d2sum0,double2 d2sum1,ulong *outul0,ulong *outul1,ulong *outul2){
double2 d2tmp;
d2tmp.x=1.0;d2tmp.y=0.0;
if (d2sum0.x<0.0){
d2sum0=addcab(d2sum0,d2tmp);
}
if (d2sum1.x<0.0){
d2sum1=addcab(d2sum1,d2tmp);
}
ulong ulsum0=0;//最上位桁
ulong ulsum1=0;//中間
ulong ulsum2=0;//最下位桁
ulong ultemp;
double dtmp;
d2sum0.x*=4503599627370496.0;//2^52
d2sum0.y*=4503599627370496.0;//2^52
dtmp=trunc(d2sum0.x);//必ず切り下げ整数切り出ししないといけない
ulsum0=(((ulong)dtmp)*(ulong)4096);
d2sum0.x-=dtmp;
d2sum0=twosum(d2sum0);//次の52bitを切り出したい
d2sum0.x*=4503599627370496.0;//2^52
if (d2sum0.x<0.0){
d2sum0.x+=4503599627370496.0;
ulsum0-=(ulong)4096;
}
ultemp=(ulong)d2sum0.x;
ulsum0|=ultemp>>((ulong)40);//これでulsum0は確定
ulsum1=(ultemp%((ulong)1<<(ulong)40))<<((ulong)24);
//ここでいったんulsum1は保留、ulsum2を埋める。d2sum1から96bit切り出す
d2sum1.x*=281474976710656.0;//2^48
d2sum1.y*=281474976710656.0;//2^48
dtmp=trunc(d2sum1.x);//必ず切り下げ整数切り出ししないといけない
ultemp=(ulong)dtmp;
d2sum1.x-=dtmp;
d2sum1=twosum(d2sum1);//次の48bitを切り出したい
d2sum1.x*=281474976710656.0;//2^48
if (d2sum1.x<0.0){
d2sum1.x+=281474976710656.0;
ultemp--;
}
ulsum2=(ultemp%((ulong)1<<(ulong)16))<<((ulong)48);
ulsum2+=(ulong)d2sum1.x;//ここはtruncを使わないほうが正解に近い
//ultempの48bit中上32bitが残っている
uint chk0=(uint)((ulsum1>>((ulong)30))%(ulong)4);//30と31bit目を切り出し
uint chk1=(uint)(ultemp>>((ulong)46));//46と47bit目を切り出し
if (chk0==chk1){//何も考えずコピーで良い
//ulsum1=(ulsum1&0xFFFFFFFF00000000)|(ultemp>>((ulong)16));
}else{
ulong last_ulsum1=ulsum1;
if (((chk0+1)%4)==chk1){//chk1が正解の数字なのでchk0側つまりulsum1とulsum0を修正しないといけない
ulsum1+=((ulong)1<<(ulong)30);
//繰り上がりあるなら
if (ulsum1<last_ulsum1)ulsum0++;
//ulsum1=(ulsum1&0xFFFFFFFF00000000)|(ultemp>>((ulong)16));
}
if (((chk0-1)%4)==chk1){//chk1が正解の数字なのでchk0側つまりulsum1とulsum0を修正しないといけない
ulsum1-=((ulong)1<<(ulong)30);
//繰り下がりあるなら
if (ulsum1>last_ulsum1)ulsum0--;
//ulsum1=(ulsum1&0xFFFFFFFF00000000)|(ultemp>>((ulong)16));
}
//これ以外のパターンは想定外、一応ないと証明できている。
}
ulsum1=(ulsum1&0xFFFFFFFF00000000)|(ultemp>>((ulong)16));
//192bit sumの完成!!!
*outul0=ulsum0;
*outul1=ulsum1;
*outul2=ulsum2;
return;
}
擬似四倍精度2つ→192bit整数へのキャスト関数が完成しました!
こんなのを毎ループ回したら激重になるに違いないと思いますが、一応オーバーラップ部分が10bitと余裕があるので、毎ループこれを行わなくても、何度か擬似四倍精度だけでイテレーションを回しても大丈夫そうです。自分の実装では32ループに1回だけこのキャストを行っています。(オーバーラップ部分は2bitあれば繰り上がり方向が判定できるので、32=2^5なので10bit-5bit=5bitとまだ余裕はあります。)
これでも計算時間はたったの1.25倍。精度は106→192bitに進化しているので実装した甲斐があったというものです。
モンゴメリ乗算
少し話は戻りべき剰余高速化のためのモンゴメリ乗算です。
なんかいろいろモンゴメリリダクションで変換しておくと剰余と同じことが乗算とビットシフトでできるよっていう内容だと理解してます。完全には理解しきれてないのでもうちょっとしたら書き直すかもです。
mul_hiを使った実装の提示をしておきます。
//モンゴメリリダクション
ulong MR64(const ulong xlo,const ulong xhi,const ulong inv,const ulong modC)
{
ulong xinv=xlo*inv;
ulong ret=mul_hi(xinv,modC);
if (xlo!=0)ret++;//分かりにくいが、xinv*modC+xloは必ずRで割り切れるので
//ret+=xhi;//これはオーバーフローするかもしれないので以下4行
ulong ans=ret+xhi;
if ((ans>=modC)|(ans<xhi)){//ans==modCの場合も同時に処理
ans-=modC;
}
return ans;
}
//a=1024のn乗MOD c、モンゴメリ乗算、最適化
ulong ExpMod64v4(ulong n,const ulong modC,const ulong inv,const ulong r2){
ulong a=1024;
ulong p=MR64(r2<<(ulong)10,r2>>(ulong)54,inv,modC);
ulong x=MR64(r2,0,inv,modC);
for(int i=0;i<64;i++){
if (n%(ulong)2==(ulong)1){
x=MR64(x*p,mul_hi(x,p),inv,modC);
}
p=MR64(p*p,mul_hi(p,p),inv,modC);
n/=(ulong)2;
if (n==(ulong)0)break;
}
return MR64(x,0,inv,modC);
}
modCを除数として、r2=(2^128)%modCを予め計算しておき、invにはinv*modC==(2^64)-1となる数を予め計算しておきます。
r2の計算には128bit % 64bitの処理が必要になるためやはりOpenCLですぐに書けないのが難点ですが、上で示したABModC64を使えばなんとかなります。
速度比較
GPUPIと比較
円周率任意桁の計算ソフトとして似たものにGPUPIという有名ベンチマークソフトがあります。CUDAとOpenCLで書かれているみたいで、GPU、CPUでも比較できるし同じNVIDIA GPU上でCUDAとOpenCLの速度対決もできます。公式サイトによるとGPUPIは計算にBellardではなくBBPを使っているようです(BBPのほうが遅いと言われているのでGPUPI不利です)。またこちらも擬似四倍精度で結果を集計しているようです。
RTX2080Tiで検証
| 桁 | GPUPI(Sec) | CLBellard(Sec) | 比 |
|---|---|---|---|
| 10億桁 | 3.424 | 0.865 | 3.96 |
| 320億桁 | 205.2 | 34.905 | 5.88 |
計算速度はなんと4~6倍!CLBellardの圧勝です。CLBellardはべき剰余の32bit超えるか超えないか問題で11億桁を境に急に重くなっていくのですが、10億桁、320億桁ともに勝利をおさめました。やったー
(余談ですがGPUPIとSuper_PIは、そもそも全桁求めるかという点で全然違うので比較するのはなんか違うなと思っています。)
y-chruncherBBP sse4 verと比較
こちらはかの有名なy-chruncherのBBP版です。BBP版といってもBBPの公式とBellardの式のどちらも選択できます。ただしsse4と書いてあるようCPU上でしか動かないです。
Core i9 9920Xで検証
| y-chruncher(Sec) | CLBellard(Sec) | 比 | |
|---|---|---|---|
| 10億桁 | 10.3 | 7.52 | 1.37 |
| 320億桁 | 355.6 | 1714 | 0.2075 |
こちらでは320億桁で惨敗、10億桁では上記理由で恐らく僅差になってます。y-chruncherではべき剰余で整数型を使ってないのか11億桁を境に遅くなるという現象が見られませんでした。またCLBellardはOpenCLで書かれており計算をうまい具合にSIMD化してくれるので今回のCPUで言えばAVX512F,DQなどの機能まで使ってくれているはずです(調べてはないですが)。
~~おしまい?~~4000兆桁以降追記(2021/5/28)
4000兆桁、1京桁、2京桁も求め終わりました。
https://toropippi.web.fc2.com/cfdjk.html
こちらのHPに詳しくまとめております。
一応結果だけ書いておくと
4000兆桁
1st :starting at 410^15
2nd :starting at 410^15-5
1st run: 5cc37dec84c20b798ba57faf5c691f340665147606e69360
2nd run: 06df35cc37dec84c20b798ba57faf5c6919f33dfbba887cb
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
1京桁
1st :starting at 110^16
2nd :starting at 110^16-5
1st run: 9077e0164b9c613fd6c7f170c99c2a6694e2534bb43554f2
2nd run: dc2ca9077e0164b9c613fd6c7f170c99b89a3fd63770a838
^^^^^^^^^^^^^^^^^^^^^^^^^^^
2京桁
1st :starting at 2×10^16
2nd :starting at 2×10^16-5
1st run: 1021b52fb719ada36b81d6cecc98c054857239d9519210bd
2nd run: 509ab1021b52fb719ada36b81d6cecc977ecf558fb98fddf
^^^^^^^^^^^^^^^^^^^^^^^^^^^