初心者向けPyTorch篇：6.多値分類

この記事は、手書き数字認識でよく使われるMNISTデータセットを題材に、多分類問題を解くニューラルネットワークをPyTorchで構築・学習させる手順を解説しています。
データの準備からモデル構築、学習ループ、評価、結果の可視化まで一通り網羅しています。モデルは28×28ピクセルの画像を入力し、3層の全結合ネットワークで10クラス（数字0～9）に分類します。

MNISTデータセットの準備

以下のコードは、MNISTデータセットをダウンロードし、学習データとテストデータに分けて準備します。

import torch
from torch import nn
import torchvision
from torchvision.transforms import ToTensor
import matplotlib.pyplot as plt
import numpy as np

# MNISTデータセットをダウンロード
train_dataset = torchvision.datasets.MNIST('data', train=True, transform=ToTensor(), download=True)
test_dataset = torchvision.datasets.MNIST('data', train=False, transform=ToTensor(), download=True)

# DataLoaderでバッチ分け
train_dataloader = torch.utils.data.DataLoader(train_dataset, batch_size=64, shuffle=True)
test_dataloader = torch.utils.data.DataLoader(test_dataset, batch_size=64)

ここで、ToTensorを使用して画像をテンソル形式に変換し、データローダーを使ってデータを効率的に扱えるようにしています。

データの可視化

次に、学習データの一部を可視化します。

imgs, labels = next(iter(train_dataloader))  # データローダーから最初のバッチを取得

print(imgs.shape)
# torch.Size([64, 1, 28, 28])

# 10個の画像をプロット
plt.figure(figsize=(10, 1))
for i, img in enumerate(imgs[:10]):
    np_img = img.numpy().squeeze()  # 次元を削減して画像表示可能に
    plt.subplot(1, 10, i+1)
    plt.imshow(np_img, cmap='gray')
    plt.axis('off')

PyTorchで画像データを扱う場合、少し特殊です。画像データの形状は一般的に(Channel, Height, Width)の順に構成されます。ここのtorch.Size([64, 1, 28, 28])の解説はこちら

• Batch（64）: 1回の学習ステップで処理する画像の枚数
• Channel（1）: カラーチャネル数。グレースケール画像では1、RGB画像は3
• Height（28）: 画像の縦方向のピクセル数
• Width（28）: 画像の横方向のピクセル数

出力画像：

print(labels[:10])  # 10個のラベルを表示
# tensor([1, 6, 1, 0, 2, 2, 4, 3, 1, 2])

画像はラベルの数字と一致していることがわかります。

ニューラルネットワークモデルの定義

次に、MNISTデータセット用のシンプルな3層全結合ネットワークを定義します。

class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear_1 = nn.Linear(28*28, 128)  # 入力層（28x28画素 → 128ユニット）
        self.linear_2 = nn.Linear(128, 64)    # 隠れ層（128ユニット → 64ユニット）
        self.linear_3 = nn.Linear(64, 10)     # 出力層（64ユニット → 10クラス）

    def forward(self, x):
        x = x.view(-1, 28*28)  # 入力画像を1次元に変換
        x = torch.relu(self.linear_1(x))  # ReLU活性化関数
        x = torch.relu(self.linear_2(x))
        logits = self.linear_3(x)         # 最終層の出力
        return logits

多値分類モデルでCrossEntropyLossを損失関数を使う場合、最終層の出力には活性化関数不要です。
引数解説：

• 28×28: 画像データ（28×28ピクセル）の全ピクセルを1次元ベクトルに変換し、入力層の次元数として使用します
• 128: 自由に設定可能です。入力層の出力を受け取る中間層のノード数です。モデルの表現力に影響を与える部分です
• 64: 自由に設定可能です。さらに次の中間層のノード数です。層を深くすることで特徴抽出の精度を高めます
• 10: 出力層のノード数で、分類するクラス数に対応しています（ここでは数字0～9の10クラス）

これらの設定により、モデルは入力画像を複数の中間層を通じて圧縮し、最終的にクラスごとの確率を出力します。

学習ループの定義

モデルの学習と評価を行う関数を作成します。

# 学習用関数
def train(dataloader, model, loss_fn, optimizer):
    total_loss, total_correct = 0, 0
    for x, y in dataloader:
        x, y = x.to(device), y.to(device)
        y_pred = model(x)  # モデルによる予測
        loss = loss_fn(y_pred, y)  # 損失計算
        optimizer.zero_grad()  # 前回の勾配計算結果をリセット
        loss.backward()  # 勾配計算
        optimizer.step()  # パラメータ更新
        total_loss += loss.item()  # 累計損失
        total_correct += (y_pred.argmax(1) == y).sum().item()  # 累計正解数
    return total_correct / len(dataloader.dataset), total_loss / len(dataloader)

評価関数も同様に定義します。

# 評価用関数
def test(dataloader, model, loss_fn):
    total_loss, total_correct = 0, 0
    with torch.no_grad():
        for x, y in dataloader:
            x, y = x.to(device), y.to(device)
            y_pred = model(x)
            loss = loss_fn(y_pred, y)
            total_loss += loss.item()
            total_correct += (y_pred.argmax(1) == y).sum().item()
    return total_correct / len(dataloader.dataset), total_loss / len(dataloader)

モデル学習

次に、学習と評価を行うファンクションを作成します。

def fit(epochs, train_dataloader, test_dataloader, model, loss_fn, optimizer):
    for epoch in range(epochs):
        train_acc, train_loss = train(train_dataloader, model, loss_fn, optimizer)
        test_acc, test_loss = test(test_dataloader, model, loss_fn)
        print(f"Epoch {epoch+1}: Train Acc: {train_acc*100:.2f}%, Train Loss: {train_loss:.4f}, Test Acc: {test_acc*100:.2f}%, Test Loss: {test_loss:.4f}")

最後に学習を実行します。

# デバイスの設定
device = 'cuda' if torch.cuda.is_available() else 'cpu'

# モデル、損失関数、最適化アルゴリズムの準備
model = Model().to(device)
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.001)

# 学習を実行
epochs = 50
fit(epochs, train_dataloader, test_dataloader, model, loss_fn, optimizer)

実行ログ：

epoch:  0, train loss: 2.29111, train acc: 12.3%, test loss: 2.27806, test acc: 16.7%
epoch:  1, train loss: 2.26400, train acc: 32.0%, test loss: 2.24456, test acc: 48.4%
epoch:  2, train loss: 2.22359, train acc: 55.2%, test loss: 2.19217, test acc: 61.2%
epoch:  3, train loss: 2.15901, train acc: 61.5%, test loss: 2.10740, test acc: 64.3%
epoch:  4, train loss: 2.05115, train acc: 63.5%, test loss: 1.96535, test acc: 65.9%
epoch:  5, train loss: 1.87447, train acc: 65.9%, test loss: 1.74258, test acc: 68.8%
epoch:  6, train loss: 1.61820, train acc: 68.9%, test loss: 1.44944, test acc: 72.7%
epoch:  7, train loss: 1.32459, train acc: 72.8%, test loss: 1.16300, test acc: 76.4%
epoch:  8, train loss: 1.07261, train acc: 77.0%, test loss: 0.94667, test acc: 79.3%
epoch:  9, train loss: 0.89265, train acc: 79.7%, test loss: 0.79977, test acc: 81.2%
epoch: 10, train loss: 0.77058, train acc: 81.5%, test loss: 0.69974, test acc: 83.0%
epoch: 11, train loss: 0.68594, train acc: 82.8%, test loss: 0.62923, test acc: 84.1%
epoch: 12, train loss: 0.62457, train acc: 83.9%, test loss: 0.57743, test acc: 85.0%
epoch: 13, train loss: 0.57814, train acc: 84.8%, test loss: 0.53643, test acc: 85.7%
epoch: 14, train loss: 0.54177, train acc: 85.6%, test loss: 0.50524, test acc: 86.5%
epoch: 15, train loss: 0.51250, train acc: 86.3%, test loss: 0.47874, test acc: 87.1%
epoch: 16, train loss: 0.48847, train acc: 86.8%, test loss: 0.45754, test acc: 87.6%
epoch: 17, train loss: 0.46841, train acc: 87.3%, test loss: 0.43952, test acc: 87.9%
epoch: 18, train loss: 0.45155, train acc: 87.7%, test loss: 0.42463, test acc: 88.3%
epoch: 19, train loss: 0.43716, train acc: 88.1%, test loss: 0.41107, test acc: 88.7%
epoch: 20, train loss: 0.42448, train acc: 88.4%, test loss: 0.40032, test acc: 89.0%
epoch: 21, train loss: 0.41381, train acc: 88.6%, test loss: 0.38988, test acc: 89.2%
epoch: 22, train loss: 0.40424, train acc: 88.8%, test loss: 0.38158, test acc: 89.4%
epoch: 23, train loss: 0.39553, train acc: 89.0%, test loss: 0.37443, test acc: 89.3%
epoch: 24, train loss: 0.38797, train acc: 89.2%, test loss: 0.36703, test acc: 89.6%
epoch: 25, train loss: 0.38110, train acc: 89.3%, test loss: 0.36087, test acc: 89.7%
epoch: 26, train loss: 0.37497, train acc: 89.4%, test loss: 0.35511, test acc: 89.9%
epoch: 27, train loss: 0.36911, train acc: 89.6%, test loss: 0.35023, test acc: 89.9%
epoch: 28, train loss: 0.36401, train acc: 89.7%, test loss: 0.34506, test acc: 90.0%
epoch: 29, train loss: 0.35903, train acc: 89.8%, test loss: 0.34083, test acc: 90.0%
epoch: 30, train loss: 0.35458, train acc: 89.9%, test loss: 0.33695, test acc: 90.3%
epoch: 31, train loss: 0.35034, train acc: 90.1%, test loss: 0.33320, test acc: 90.3%
epoch: 32, train loss: 0.34621, train acc: 90.1%, test loss: 0.32915, test acc: 90.5%
epoch: 33, train loss: 0.34232, train acc: 90.2%, test loss: 0.32576, test acc: 90.5%
epoch: 34, train loss: 0.33874, train acc: 90.3%, test loss: 0.32263, test acc: 90.6%
epoch: 35, train loss: 0.33533, train acc: 90.4%, test loss: 0.31956, test acc: 90.7%
epoch: 36, train loss: 0.33219, train acc: 90.5%, test loss: 0.31656, test acc: 90.8%
epoch: 37, train loss: 0.32890, train acc: 90.5%, test loss: 0.31398, test acc: 90.9%
epoch: 38, train loss: 0.32584, train acc: 90.7%, test loss: 0.31088, test acc: 91.1%
epoch: 39, train loss: 0.32303, train acc: 90.7%, test loss: 0.30811, test acc: 91.1%
epoch: 40, train loss: 0.32017, train acc: 90.8%, test loss: 0.30561, test acc: 91.1%
epoch: 41, train loss: 0.31750, train acc: 90.9%, test loss: 0.30296, test acc: 91.2%
epoch: 42, train loss: 0.31485, train acc: 90.9%, test loss: 0.30043, test acc: 91.3%
epoch: 43, train loss: 0.31228, train acc: 91.0%, test loss: 0.29877, test acc: 91.4%
epoch: 44, train loss: 0.30952, train acc: 91.1%, test loss: 0.29637, test acc: 91.4%
epoch: 45, train loss: 0.30718, train acc: 91.2%, test loss: 0.29349, test acc: 91.5%
epoch: 46, train loss: 0.30489, train acc: 91.2%, test loss: 0.29190, test acc: 91.6%
epoch: 47, train loss: 0.30247, train acc: 91.3%, test loss: 0.28997, test acc: 91.6%
epoch: 48, train loss: 0.30007, train acc: 91.4%, test loss: 0.28766, test acc: 91.7%
epoch: 49, train loss: 0.29781, train acc: 91.4%, test loss: 0.28632, test acc: 91.7%

結果の可視化

学習中の損失と精度を可視化することができます。

# 精度と損失をプロット
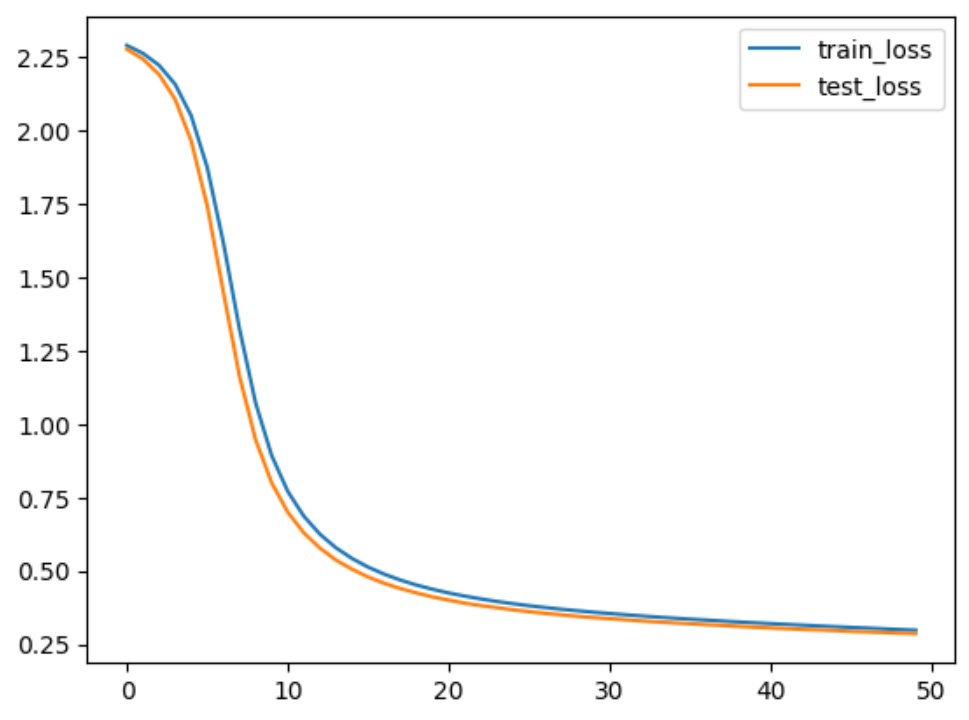
plt.plot(range(epochs), train_loss, label="train_loss")
plt.plot(range(epochs), test_loss, label="test_loss")
plt.legend()
plt.show()

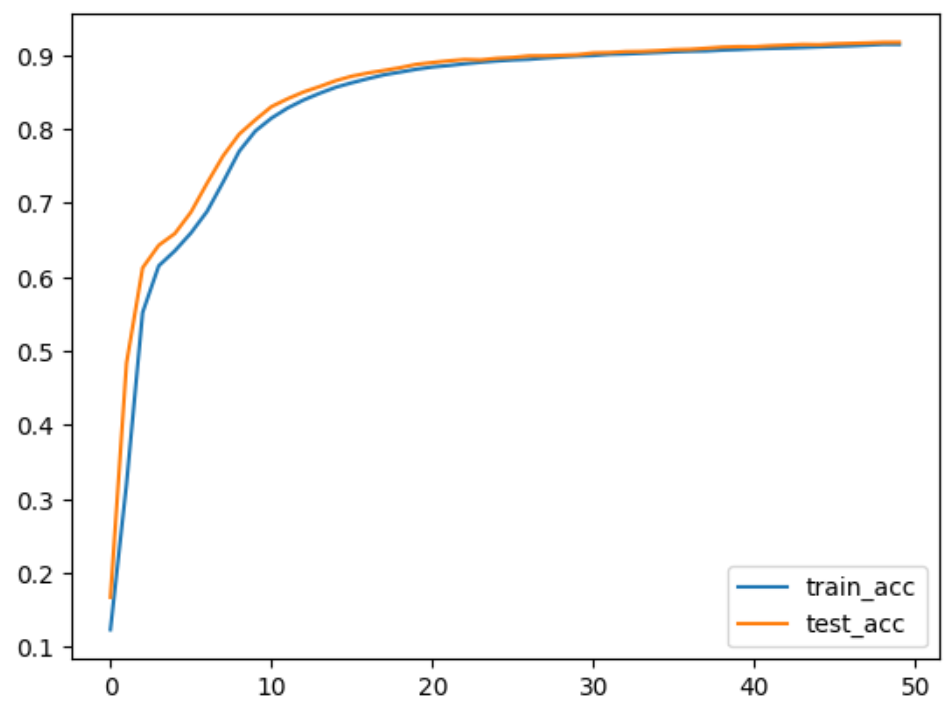
plt.plot(range(epochs), train_acc, label="train_acc")
plt.plot(range(epochs), test_acc, label="test_acc")
plt.legend()
plt.show()

考察

• 損失の変化: 学習初期では損失（loss）が急激に減少しており、モデルが効率的にパターンを学習していることがわかります。その後、エポックが進むにつれて損失の減少が緩やかになり、最終的に落ち着く傾向が見られます。これは、モデルが収束に近づいていることを示しています
• トレーニングデータとテストデータの精度: 学習時の精度（train accuracy）とテスト時の精度（test accuracy）の差が小さく、過学習（オーバーフィット）が発生していないことが確認できます。これはモデルが汎化性能を維持できている理想的な状態です

結論

このコードでは、MNISTデータセットを使用したシンプルな多分類モデルを構築し、学習プロセスを説明しました。結果として、オーバーフィットがなく、精度の改善の余地があることが分かります。