TDA(topological data analysis)で、一次元の輪、2次元の空洞を数える
パッケージ
library(TDA)
library(foreach)
library(ggplot2)
library(tidyverse)
library(readxl)
SDの計算
下の画像のようにROIをとってImageJで各ROIのStDvを取得

全ROIの平均値をSDとする
> read_excel("C:/Users/owner/Desktop/sd.xlsx")
# A tibble: 55 x 3
Area StdDev mA
<dbl> <dbl> <dbl>
1 746 25.2 50.0
2 746 21.9 50.0
3 746 21.8 50.0
4 746 21.1 50.0
5 746 24.1 50.0
6 746 17.6 100
7 746 14.6 100
8 746 15.1 100
9 746 15.0 100
10 746 17.2 100
# ... with 45 more rows
read_excel("C:/Users/owner/Desktop/sd.xlsx") %>%
select(-Area) %>%
group_by(mA) %>%
summarise(SD = mean(StdDev)) -> SD_tbl
> SD_tbl
# A tibble: 11 x 2
mA SD
<dbl> <dbl>
1 50.0 22.8
2 100 15.9
3 150 13.2
4 200 11.2
5 250 10.1
6 300 9.58
7 350 8.46
8 400 7.99
9 450 7.68
10 500 7.32
11 550 7.13
ImageJで画像の座標を取得
Save XY Coordinatesで(x,y,z,Value)を取得
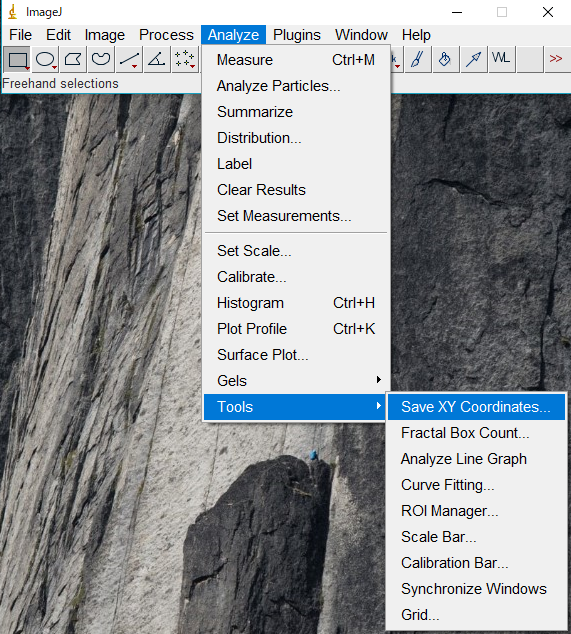
今回は管電流が50から550mAまで50mA刻みのCT水ファントム画像を用いました。だから11枚の画像
read_delim("20170930.txt",
"\t",escape_double = FALSE,
col_names = FALSE,
col_types = cols(X4 = col_double()),
trim_ws = TRUE) %>%
rename(x = V1, y = V2, z = V3, HU = V4) %>%
as.tbl() %>%
dplyr::filter(HU >= 100) %>%
group_by(z) %>%
nest() -> dat
slice_Number <- seq_along(dat$z) ## foreachで使う
> dat$data[[1]]
# A tibble: 57,275 x 3
x y HU
<int> <int> <dbl>
1 243 123 293
2 244 123 302
3 245 123 297
4 246 123 302
5 247 123 313
6 248 123 268
7 249 123 296
8 250 123 289
9 251 123 319
10 252 123 287
# ... with 57,265 more rows
TDA
TDA::alphashapeDiag()を使って計算
shapeDiag <- foreach(i = slice_Number) %do% alphaShapeDiag(dat$data[[i]])
パーシステント図(PD)をデータフレームに変換
mutate()でDeathとBirthの差を付け加える
shapeDiag_df <- foreach(i = slice_Number) %do% {
tibble::tibble(
Dimension = as.factor(shapeDiag[[i]]$diagram[,1]),
Birth = shapeDiag[[i]]$diagram[,2],
Death = shapeDiag[[i]]$diagram[,3]
) %>%
mutate(SuvivalInterval = Death - Birth)
}
PDの座標からDimension毎に個数(holes)、生存半径区間のMax,Min,Median,Meanの集計
summarise_df <- foreach(i = slice_Number, .combine = rbind) %do% {
shapeDiag_df[[i]] %>%
group_by(Dimension) %>%
summarise(.,
holes = n(),
Max = max(SuvivalInterval),
Min = min(SuvivalInterval),
Median = median(SuvivalInterval),
Mean = mean(SuvivalInterval)
) %>%
mutate(.,mAs = mAs[i])
}
生成される半径が各画像のSD以上またはSD以下で区切って集計
Birth ≦ SD
summarise_sdun_df <- foreach(i = slice_Number, .combine = rbind) %do% {
shapeDiag_df[[i]] %>%
dplyr::group_by(.,Dimension) %>%
dplyr::filter(.,Birth <= SD_tbl$SD[i]) %>%
dplyr::summarise(.,
holes = n(),
Max = max(SuvivalInterval),
Min = min(SuvivalInterval),
Median = median(SuvivalInterval),
Mean = mean(SuvivalInterval)
) %>%
mutate(.,mAs = mAs[i])
}
Birth ≧ SD
summarise_sdov_df <- foreach(i = slice_Number, .combine = rbind) %do% {
shapeDiag_df[[i]] %>%
dplyr::group_by(.,Dimension) %>%
dplyr::filter(.,Birth >= SD_tbl$SD[i]) %>%
dplyr::summarise(.,
holes = n(),
Max = max(SuvivalInterval),
Min = min(SuvivalInterval),
Median = median(SuvivalInterval),
Mean = mean(SuvivalInterval)
) %>%
mutate(.,mAs = mAs[i])
}
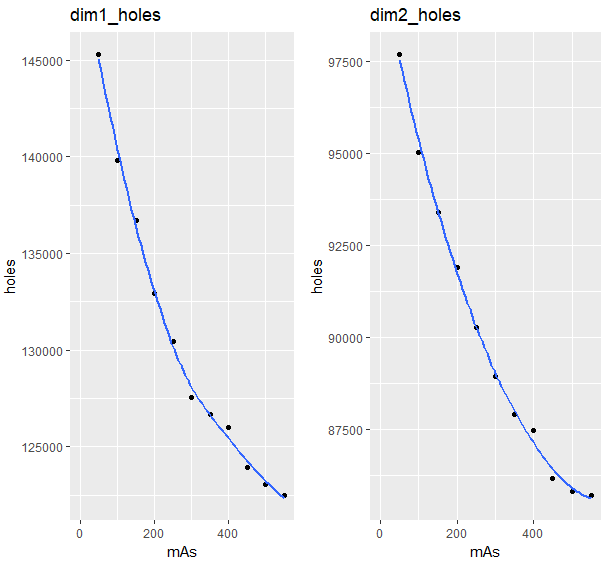
Dimension毎にネストさせてggplotでmAと穴or空洞の数(holes)の関係
## dimensionでネストさせたtbl_df
Interval_tbl <- summarise_df %>%
group_by(Dimension) %>%
nest()
## Birth <= SD
Interval_sdun_tbl <- summarise_sdun_df %>%
group_by(Dimension) %>%
nest()
## Birth >= SD
Interval_sdov_tbl <- summarise_sdov_df %>%
group_by(Dimension) %>%
nest()
dim <- seq_along(Interval_tbl$Dimension)
## ggplot_穴の数
gg_dimk_holes <- foreach(k = dim) %do% {
ggplot(Interval_tbl$data[[k]],aes(x = mAs,y = holes))+
xlim(0,550)+
geom_point()+
geom_smooth(se = FALSE,method = "loess") +
ggtitle(str_c("dim", sep = k-1, "_holes"))
}
gg_dimk_holes_sdun <- foreach(k = dim) %do% {
ggplot(Interval_sdun_tbl$data[[k]],aes(x = mAs,y = holes))+
xlim(0,550)+
geom_point()+
geom_smooth(se = FALSE,method = "loess") +
ggtitle(str_c("dim", sep = k-1, "_holes"),subtitle = "<= under_sd")
}
gg_dimk_holes_sdov <- foreach(k = seq_along(Interval_sdov_tbl$Dimension)) %do% {
ggplot(Interval_sdov_tbl$data[[k]],aes(x = mAs,y = holes))+
xlim(0,550)+
geom_point()+
geom_smooth(se = FALSE,method = "loess") +
ggtitle(str_c("dim", sep = k, "_holes"),subtitle = "over_sd")
}
各次元(Dimension)でbirth,Death が一致した行の個数(holes)を算出することでPD作成
PD_df <- foreach(i = slice_Number) %do% {
shapeDiag_df[[i]] %>%
group_by(Dimension,Birth,Death) %>%
summarise(holes = n(),
log = log(n()),
loglog = log(log(n()))
) %>%
ungroup()
}
PD_df_nest <- foreach(i = slice_Number) %do% {
shapeDiag_df[[i]] %>%
group_by(Dimension,Birth,Death) %>%
summarise(holes = n(),
log = log(n()),
loglog = log(log(n()))
) %>%
group_by(Dimension) %>%
nest()
}
重複した点があると、ggplotではPDを書くのが遅くなる。重複が7000を超える座標が多く存在するため
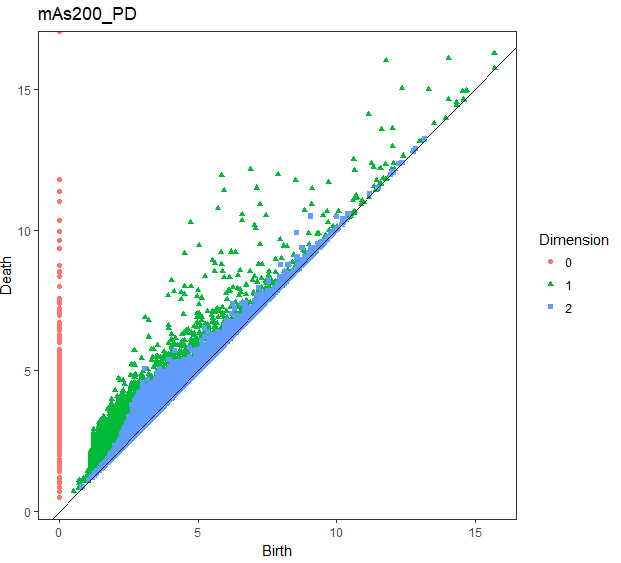
PDのプロット
## PD
gg_PD <- foreach(i = slice_Number) %do% {
PD_df[[i]] %$%
ggplot(.,aes(x = Birth, y = Death, shape = Dimension, colour = Dimension)) +
geom_point() +
geom_abline(slope = 1) +
theme_bw() +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank()
) +
ggtitle(str_c("mAs",sep = i*50,"_PD"))
}
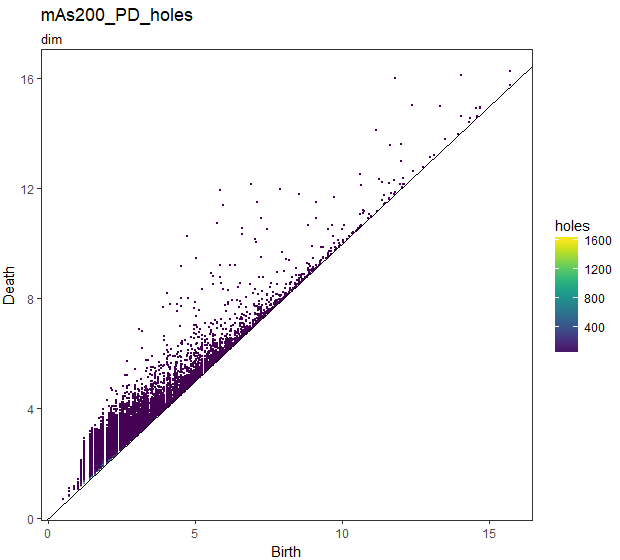
## holesは重複度が線形スケール
gg_PD_holes <- foreach(i = slice_Number) %do% {
foreach(k = dim) %do% {
PD_df_nest[[i]]$data[[k]] %$%
ggplot(.,aes(x = Birth, y = Death, colour = holes)) +
geom_point(size = rel(0.2)) +
geom_abline(slope = 1) +
theme_bw() +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank()
) +
viridis::scale_colour_viridis() +
ggtitle(str_c("mAs",sep = i*50,"_PD_holes"),subtitle = str_c("dim",sep = k))
}
}
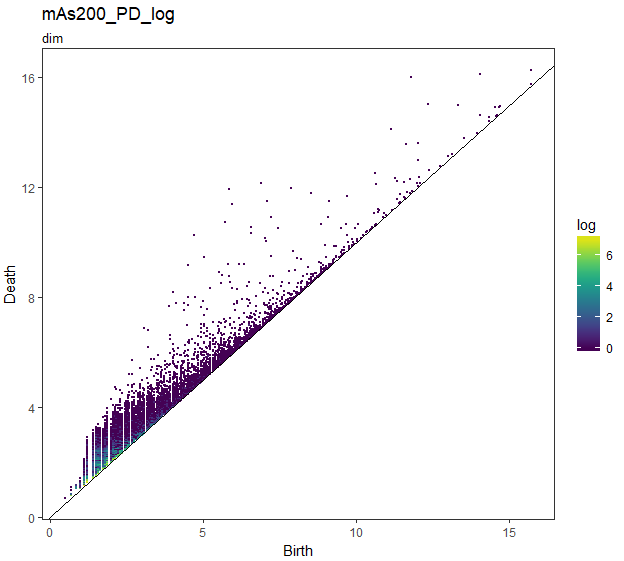
## logは重複度がlog()スケール
gg_PD_log <- foreach(i = slice_Number) %do% {
foreach(k = dim) %do% {
PD_df_nest[[i]]$data[[k]] %$%
ggplot(.,aes(x = Birth, y = Death, colour = log)) +
geom_point(size = rel(0.1)) +
geom_abline(slope = 1) +
theme_bw() +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank()
) +
viridis::scale_colour_viridis() +
ggtitle(str_c("mAs",sep = i*50,"_PD_log"),subtitle = str_c("dim",sep = k))
}
}
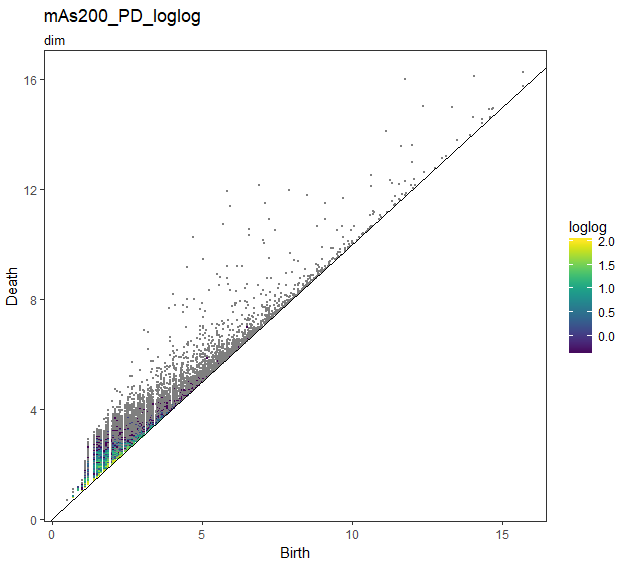
## loglogは重複度loglogスケール
gg_PD_loglog <- foreach(i = slice_Number) %do% {
foreach(k = dim) %do% {
PD_df_nest[[i]]$data[[k]] %$%
ggplot(.,aes(x = Birth, y = Death, colour = loglog)) +
geom_point(size = rel(0.1)) +
geom_abline(slope = 1) +
theme_bw() +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank()
) +
viridis::scale_colour_viridis() +
ggtitle(str_c("mAs",sep = i*50,"_PD_loglog"),subtitle = str_c("dim",sep = k))
}
}
loglogスケールでは、log1 = 0 なので log(log(1)) = Inf になりInfの部分、すなわち重複していないPDの点はグレーで表示されます