経路探索の代表的なアルゴリズムであるダイクストラ法とA*探索の、探索過程を可視化してみました。
アルゴリズムの解説
ダイクストラ法はスタートから全方位に探索してスタートから近い順に経路を確定させていき、ゴールに到達するまでこれを繰り返します。A*探索はゴールまでの距離を推定するヒューリスティック関数を用いて探索を効率化します。
A*探索では、探索ノードnに対して評価値f(n) = g(n) + h(n)が小さい順に処理します。ここで
-
g(n)= スタートから探索ノードnまでの実際の経路コスト -
h(n)= 探索ノードnからゴールまでの推定経路コスト (ヒューリスティック)
です。探索が終了するまでゴールまでの経路コストはわからないので、h(n)をどう与えるかというところで探索の効率が変わってくるのですが、ユークリッド距離を使用した幾何学的な最短経路探索ではゴールまでの直線距離を使うことができます。また、h(n) = 0の場合がダイクストラ法になります。
評価値f(n)が小さい順に探索ノードを取り出すことが必要ですが、単純に配列に入れると、最小値を検索するとき・要素を削除するときに配列の長さに比例した時間がかかり、あまり効率が良くありません。要素の追加・最小値の検索と削除を高速に(対数時間で)処理するデータ構造は “優先順位付きキュー (priority queue)” と呼ばれ、2分ヒープによる実装がもっとも有名です。
探索コード
A*探索の Javascript コードを以下に示します1。元のコードをここに記述しやすいように変更しています。queueはfを評価値とする優先順位付きキューです。
// すべての頂点に Closed でないとマークする
for (let vertex of vertices)
vertex.isClosed = false;
let start_node = {};
start_node.parent = null;
start_node.target = start;
start_node.g = 0;
start_node.f = 0; // 計算不要(すぐにキューから取り除かれるため)
let queue = new PriorityQueue();
queue.push(start_node);
while (!queue.isEmpty()) {
// 最小の評価値 f をもつ探索ノードを取り出して、queue から削除する
let node = queue.pop();
// node がすでに Closed な頂点を指している場合は無視する
if (node.target.isClosed) continue;
// node が指す頂点に Closed とマークする
node.target.isClosed = true;
// スタートから node.target への最短経路は node.parent から来た
node.target.previous = node.parent;
// ゴールに到達したら、来た道をたどって経路を完成させる
if (node.target === goal) {
let total_path = [];
let vertex = goal;
while (vertex !== null) {
total_path.push(vertex);
vertex = vertex.previous;
}
return total_path;
}
// node.target に隣接する各ノードについて...
for (neighbor of node.target.neighbors) {
// Closed な頂点は展開しなくてよい
if (neighbor.isClosed) continue;
// 新たな探索ノードを生成して、キューに追加する
let new_node = {};
new_node.parent = node.target;
new_node.target = neighbor;
new_node.g = node.g + real_cost(node.target, neighbor);
new_node.f = new_node.g + heuristic_cost(neighbor, goal);
queue.push(new_node);
}
}
出発地点からの最短経路が確定している頂点にはClosedとマークします。Closedな頂点には最短経路が直前にどの頂点を通ったかを記録します。これを出発地点までたどることで最短経路が(逆向きで)得られます。
この情報はグラフデータの頂点に記録することもできますが、並列実行するときなどグラフデータに記録したくないときはHashMap的なものを使う形になると思います。後者の場合、HashMapにキーが存在する頂点が Closed となりますので、Closed であることを単独で管理する必要はありません。ここでは頂点に直接記録しています。なお、キューに挿入済みだが Closed でない頂点を Open であるといいます。
ここで探索ノードsearch_nodeはグラフの頂点とは異なることに注意してください。search_nodeは対応する頂点targetのほかに、どの頂点から来たかを示すparentを保持しています。targetへの経路を複数キューに入れておき、その中でキューから最初に出てきたsearch_nodeに対応するparentが、最短経路がどこから来たのかを表します。なぜなら、targetが同じならヒューリスティックhの値は等しいので、評価値f=g+hが最小というのは経路コストgが最小であるからです。
※インターネットで調べると探索ノードがparentを保持していない実装例も結構ありました。この場合、Openな頂点に対しては、新たに得られたfとそれまでのfを比較し、必要に応じてf, gと経路を更新する必要があります2。したがって、使用する priority queue は優先順位の変更、または要素の削除に対応している必要があります。(なお隣接頂点間の経路コストがすべて等しい場合、これは起こらないので無視でき、また単なる幅優先探索で計算できます。)上の擬似コードで示した手法ではこれは必要ありませんが、メモリ使用量は少し増えると思います。
許容的ヒューリスティック
すべての経路を調べ尽くしたわけではなく、経路コストgが最小といってもsearch_nodeが生成された中での最小なので、「本当にこれが最短経路か?」という疑問が出てきます。
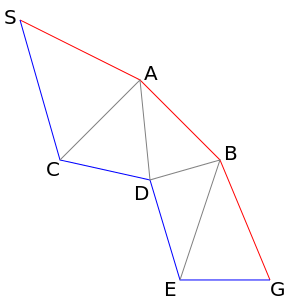
実は、ヒューリスティックがゴールまでの実際の経路コストを上回ることがない、という許容的(admissible) と呼ばれる条件を満たせば、A*探索は常に真の最短経路を見つけることが保証されます。これを理解するため、次の図を考えます。
S から G への最短経路を赤の経路S→A→B→Gとします。この経路を進むときの探索ノードの評価値を考えると、
f(S→A) = g(S→A) + h(A) ≤ g(S→A→B→G)
f(S→A→B) = g(S→A→B) + h(B) ≤ g(S→A→B→G)
f(S→A→B→G) = g(S→A→B→G) + h(G) = g(S→A→B→G)
となります(探索ノードを経路で表しています)。ここで、最短ではない経路、例えばS→C→D→E→Gを考えます。
f(S→C→D→E→G) = g(S→C→D→E→G) > g(S→A→B→G)
なので、この値はf(S→A)やf(S→A→B)より大きくなり、したがってS→C→D→E→Gの経路が完成する前に
- (A がClosedになる) → (B がClosedになる) → (S→A→B→G の経路が完成する)
が起こり、最短経路S→A→B→Gが先に見つかることになります。これはS→C→D→E→Gの代わりに任意の非最短経路について成り立つので、非最短経路が先に見つかることはありません。もしヒューリスティックが許容的でなければ、
f(S→A) > f(S→C→D→E→G)
のようなことが起こり得ます。この場合、頂点Aの評価値の大きさがボトルネックになって S→A→B→G の経路を見つけられないことになります。
直線距離によるヒューリスティックは許容的なので、この場合のA*探索が見つける経路は真の最短経路になります。
成果物
成果物はこちら。Google Chrome, Firefox, Safari, Microsoft Edge で動作確認済みですが、Microsoft Edge ではタッチパネルには非対応となります。ES6で書いているため Internet Explorer には対応しておりません。
緑色で表示した辺は SearchNode が生成された辺を表します。また、2点間の経路探索のほかに、1点を指定して最短経路のツリーを表示する機能も用意しました。モデルは有名な Stanford Bunny です。
ソースコードはこちらにあります。
使用した言語・ライブラリ
ブラウザ上で体験できるように、言語は Javascript を採用しました3。
JavaScript には標準の priority queue が無いので、mourner 氏の tinyqueue を使用しました。
可視化には three.js を使用しました。これは WebGL をラップして簡単に使えるようにしたもので、シェーダーなどを書かなくても使えるようになっています。グラフィックスオブジェクトをライブラリが保持して描画する、Retained Mode タイプのライブラリです。
実行例
ダイクストラ法とA*探索の比較


経路が直線的であれば、探索の効率は大きく違います。
ゴールを少し動かしただけで経路が大きく変わる例 (A*探索)


尻尾側がゴールです。ゴールを隣の頂点に動かすと経路が大きく変わることがわかります。
また、この例では直線距離と真の距離との誤差が大きいため、A*探索でもかなり広範囲に探索していることがわかります。
上の状況を最短経路木で観察する

尻尾に到達する経路が両脇を通っていることがわかります。
参考資料
- A* search algorithm - Wikipedia
- エージェントアプローチ 人工知能 第2版