はじめに
形状処理の勉強をしていたが、本を読むだけではあまりピンとこなかったのでプログラミングしてみようと思い立ちやってみました。
ベジェ曲線とは
ベジェ曲線は制御点$P_i$を結んでできる制御ポリゴン内に作られる曲線形状のこと。
制御点とパラメータによってベジェ曲線を構成する1点が定義され、それらを繋ぐと下図のようなベジェ曲線が描ける。
青点が制御点です。
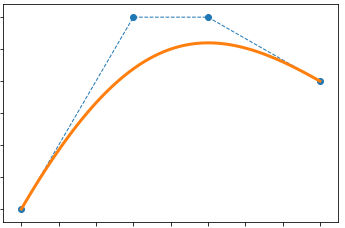
ベジェ曲線の計算
今回は2次元空間に描かれるベジェ曲線を対象にしています。
なので、座標値の成分は$(X_i, Y_i)$です。
まず、ベジェ曲線は以下の数式で定義されます。
この数式では、$t$が決まるとベジェ曲線上の点$P(t)$を計算することができます。
0~1の範囲で$t$を変化させて点$P(t)$を計算し、それぞれを繋ぐとベジェ曲線になります。
P(t) = \sum_{i=0}^{N}B_{N,i}(t)Q_i \tag{1}
B_{n,i}(t) = \begin{pmatrix}n\\i\end{pmatrix}t^i(1-t)^{n-i} \tag{2}
$t$とか、$N$とか、色々記号が出てきますが、それぞれの意味は以下の通りです。
-
$t$
媒介変数とかパラメータと呼ばれます。
とりうる範囲は$0 \leq t \leq 1$です。 -
$N$
次数のことです
例えば次数3だと3次ベジェ曲線が描けます。
次数を上げていくと複雑な形状になっていきます。 -
$Q_i$
制御点です。
上図で言うと青点のことです。 -
二項係数
$B_{n,i}(t)$ の右辺で計算される係数部分は二項係数といい、以下の式で計算されます。
\begin{pmatrix} n\\i \end{pmatrix} = {_n\mathrm{C}_k=\frac{n!}{k!(n-k)!} } \tag{3}
また、$(2)$はバーンスタイン多項式と呼ばれています。
プログラム
実装したpythonスクリプトは以下の通りです。
- ベジェ曲線計算部分
# 2項係数計算
def BiCoe(n, k):
if n < k :
return -1
return math.factorial(n) / (math.factorial(k) * math.factorial((n - k)))
# Bernstein多項式
def Bernstein(n, i, t):
return BiCoe(n, i) * np.power((1-t), (n-i)) * np.power(t, i)
# ベジェ曲線
def BezierCurve(points, t):
Gt = 0
n = len(points) - 1
for k, point in enumerate(points):
Gt += point * Bernstein(n, k, t)
return Gt
- ベジェ曲線描画部分
# ベジェ曲線を描画
def DrawBezierCurve(points):
x = np.arange(0, 1, 0.01, dtype=np.float32)
x = np.append(x, 1.0)
gt = [BezierCurve(points, t) for t in x]
gt_x = [g[0] for g in gt]
gt_y = [g[1] for g in gt]
ct_x = [ct[0] for ct in points]
ct_y = [ct[1] for ct in points]
plt.plot(ct_x, ct_y, linestyle='dashed', linewidth=1)
plt.plot(gt_x, gt_y, linewidth = 3)
plt.scatter(ct_x, ct_y)
おわりに
本読んでいるときは、「この数式で曲線が書けるの~?」なんて愚かなことを思ってましたが、実際に実装してベジェ曲線を描いてみると理論と実装が結びついて理解がより深まったと思います。
数学ヨワヨワな私はちょっとしたことで調べまくり、理解するまでにやたらと時間がかかりました。。。
例えば、$(2)$の式を見て係数部分が二項係数だって知るのに30分くらいかかりました。(爆)
今後も頑張って勉強します。