0. はじめに
2020年9月7日にAtCoder公式のアルゴリズム集 AtCoder Library (ACL)が公開されました。
私はACLに収録されているアルゴリズム、データ構造のほとんどが初見だったのでいい機会だと思い、アルゴリズムの勉強からPythonでの実装までを行いました。
この記事では Fenwick Tree (フェニック木) をみていきます。
対象としている読者
- Fenwick-Treeってなに?という方。
- ACLのコードを見てみたけど何をしているのかわからない方。
- C++はわからないのでPythonで読み進めたい方。
参考にしたもの
フェニック木の仕組みについて
- Binary indexed tree (スライド) 非常に分かりやすいです
- Wikipedia - フェニック木
ビット演算について
1. フェニック木とは
「フェニック木とは何か?」を理解するためにまずは次の問題を考えてみます。
長さ$N$の数列 $a_1, a_2, \cdots, a_N$ が与えられ、この数列に対する以下の2種類のクエリがたくさん投げられます。これを処理してください。
- add : $i, x$ が与えられるので、$a_i$ に $x$ を加算する。
- sum : $i$ が与えられるので、先頭から $i$ 番目までの和を求める。
なお以降では、与えられる値を明示して add(i, x), sum(i) と書くこともあります。
1.1. まずは愚直解
まずは問題に書かれている通りに考えてみます。クエリaddは
a_i \leftarrow a_i+x
とすればいいので計算量 $O(1)$ で処理できます。
一方、クエリsumは
a_1+a_2+\cdots+a_i
を計算する必要があるので、計算量は $O(N)$ となります。
1.2. 部分和といえば累積和
クエリsumのような数列の部分和といえば累積和が思いつくでしょう。実際、数列 $a$ の累積和をとった配列を用意すればクエリsumは $O(1)$ で処理できます。
しかし、クエリaddはどうでしょうか。数列 $a$ の1箇所を変更すると累積和を計算し直す必要があるので結局、計算量は $O(N)$ となります。
1.3. そんなときにフェニック木
愚直解も累積和もadd,sum両方のクエリを処理するためには1回あたり計算量 $O(N)$ が必要でした。もちろんこれで間に合う場合はいいのですがもっと速くしたい。。。
そんなときに登場するのがフェニック木です。フェニック木はクエリadd, sumの両方を1回あたり $O(\log N)$ で処理できます!
フェニック木は Binary Indexed Tree(BIT) とも呼ばれます。
2. フェニック木ってどんな木?
それではフェニック木の構造を見ていきます。そのために数列 $a$ の長さとして具体的に $N=7$ の場合を考えてみましょう。
2.1. とりあえず木をつくる
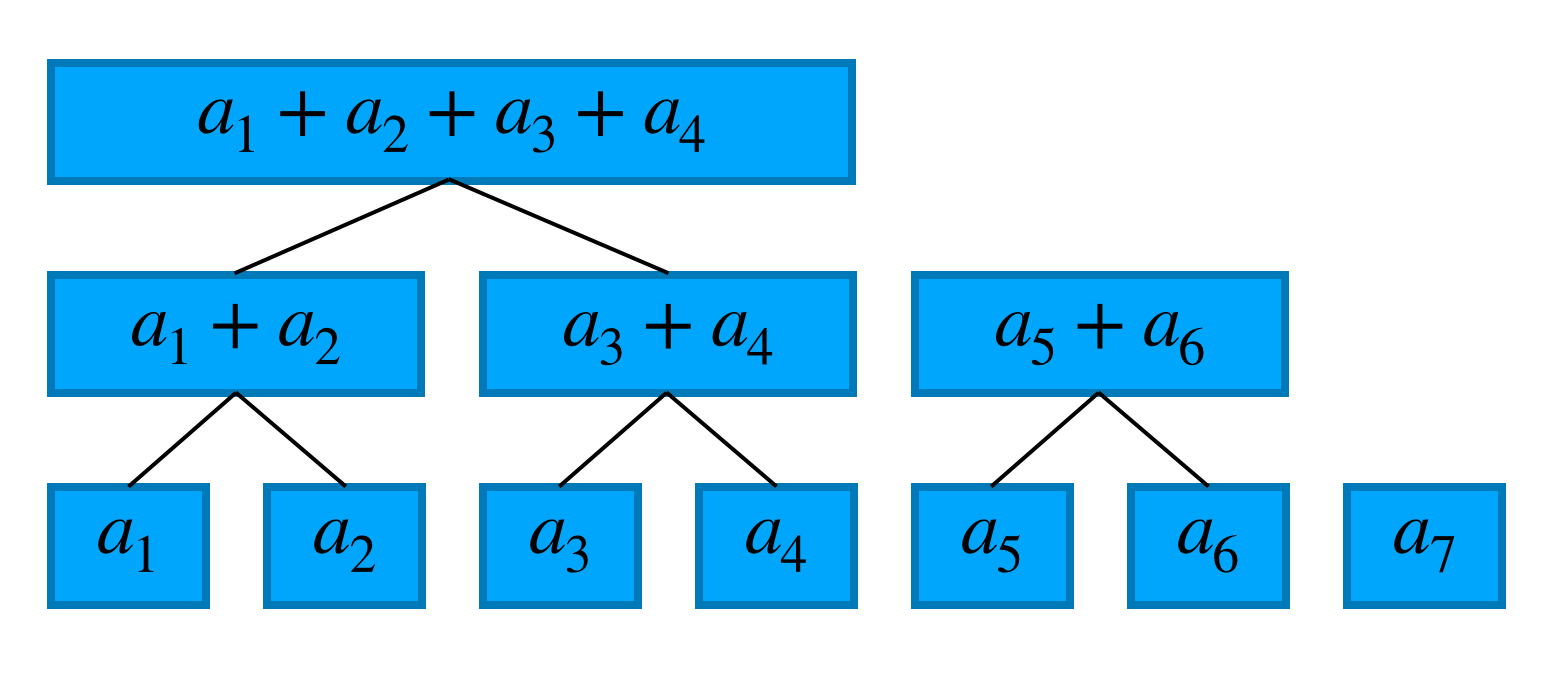
フェニック『木』というからには木構造であるはずなので数列 $a$ から木をつくります。具体的には下図のように数列の各項を葉として2項の和を親として木をつくります。
木(森?)ができたので、この木を使って前章の問題を解いてみます。
まずはクエリaddです。例として $a_3$ を更新する場合を考えましょう。$a_3$ が関係するのは3箇所あるのでこれらを更新すれば良いです。より一般的には更新すべき場所は木の高さ程度の数あります。この木の高さはおおよそ $\log N$ なので計算量は $O(\log N)$ となります。
クエリsumはどうでしょうか。例えば、7番目までの和を求める場合
\sum_{i=1}^{7}{a_i}=(a_1+a_2+a_3+a_4)+(a_5+a_6)+(a_7)
なので3箇所見れば良いです。こちらも一般的には木の高さ程度の場所を見れば良いので計算量は $O(\log N)$ となります。
2.2. よりスマートに
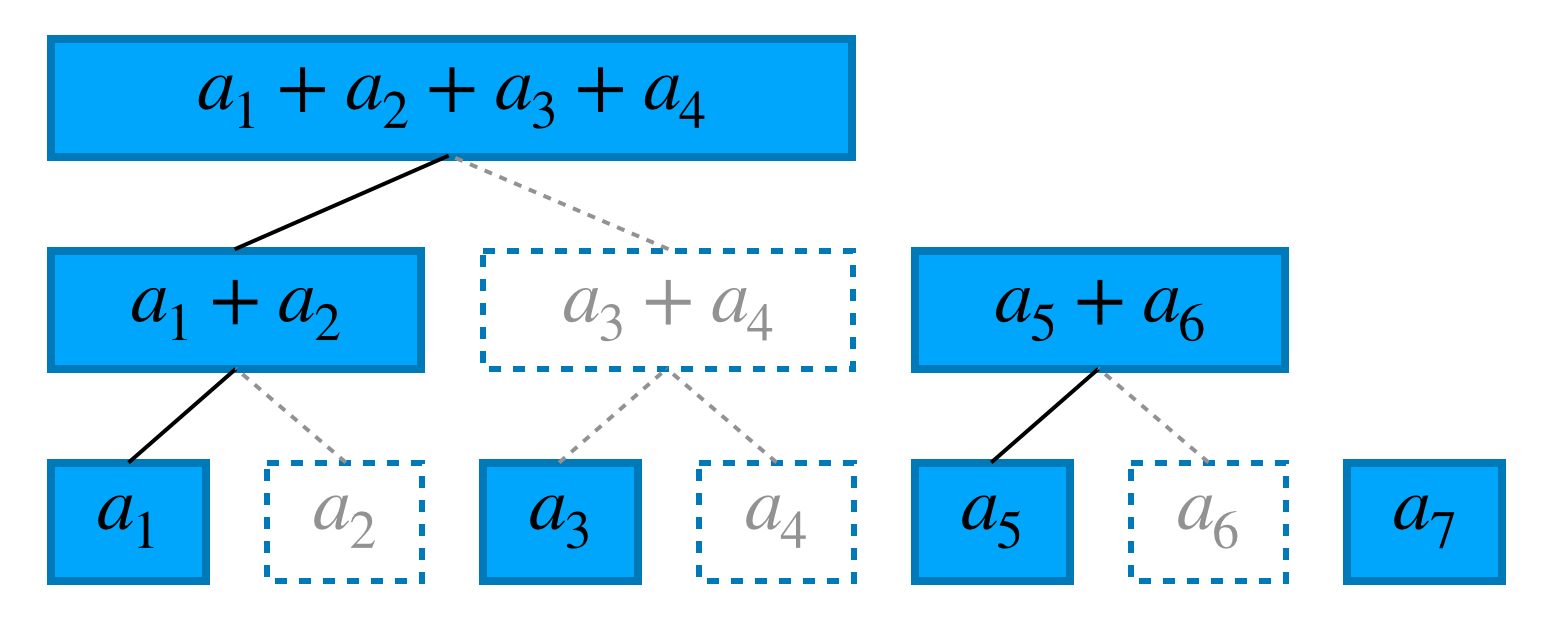
ということでadd, sum両クエリに対して $O(\log N)$ で処理ができそうです。めでたしめでたし・・・と言いたいところですが、実は先ほどつくった木には無駄があります。実際に、1番目までの和、2番目までの和、$\cdots$ 、7番目までの和と全て確認してみると一度も見ない場所がいくつかあります。それらを取り除くと下図のようになります。この中にクエリsumを処理するために必要な情報が全て入っています。(クエリaddは関係ある場所を更新するだけなので問題ないです。)
2.3. フェニック木の本当の姿
さて、ここまで「フェニック木ってどんな木?」を知るために木構造を示してきましたが、ACLのフェニック木のコードを見てみると、dataという長さ $N$ の1次元配列しかありません。木はどこにあるのでしょうか?
実はこのdataに木構造が詰まっています。具体的には配列のindexを使って「辿るべき道順」の情報を持っています。
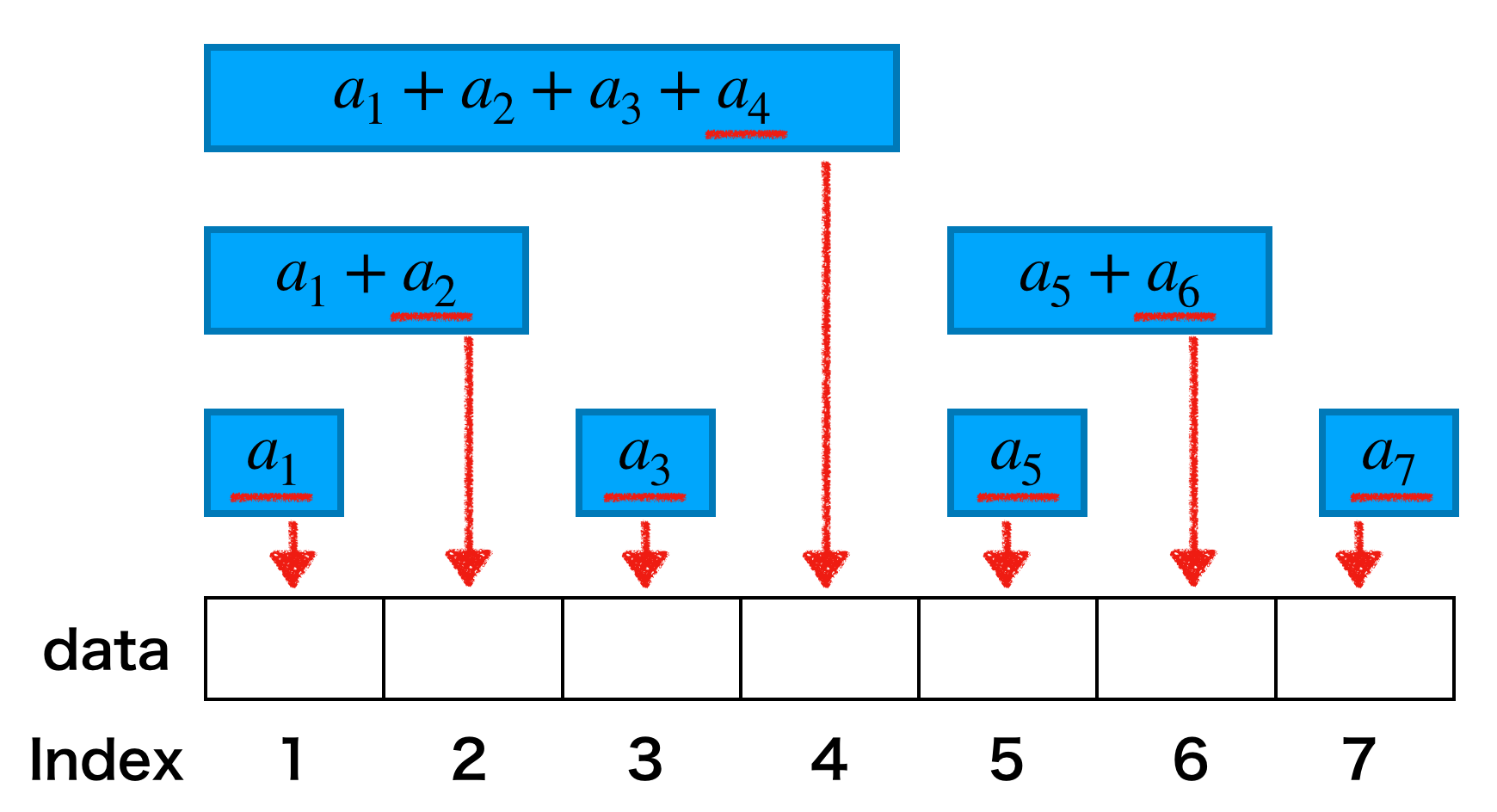
それでは、上でみた木を1次元配列に直しましょう。気づいた方もいるかもしれませんが先ほど無駄な部分を取り除いたことで残っている場所はちょうど$N$箇所になりました。そして各場所で、部分和をとるindexの最大値(下図の赤下線部)が異なります。この値を使うことでdataをつくることができます。
というわけで、フェニック木の実態は(実装上は)、部分和をなんかいい感じに詰め込んだ1次元配列だとわかりました。
3. 奇妙な配列の歩き方
我々の目的はこの奇妙な配列dataを使ってクエリadd, sumを処理することです。この章ではそれぞれのクエリで「辿るべき道順」がどのように得られるかをみていきます。
3.1. クエリadd
まずはクエリaddです。クエリadd(i, x)は $a_i$ を含む場所すべてを辿ればいいです。いくつか例をみてみましょう。
| 更新するindex | 辿るべき道順 |
|---|---|
| 1 | 1 → 2 → 4 |
| 2 | 2 → 4 |
| 5 | 5 → 6 |
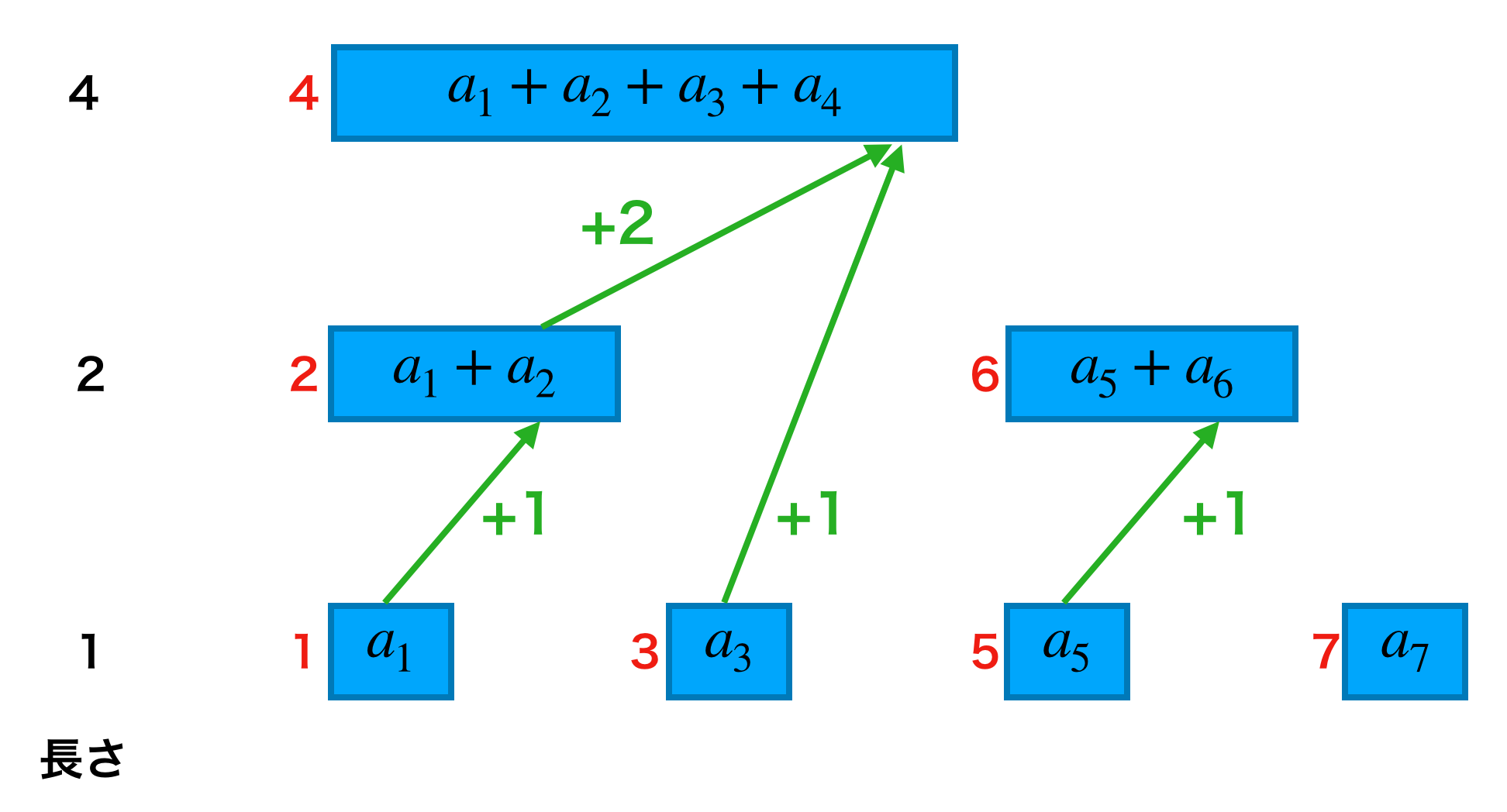
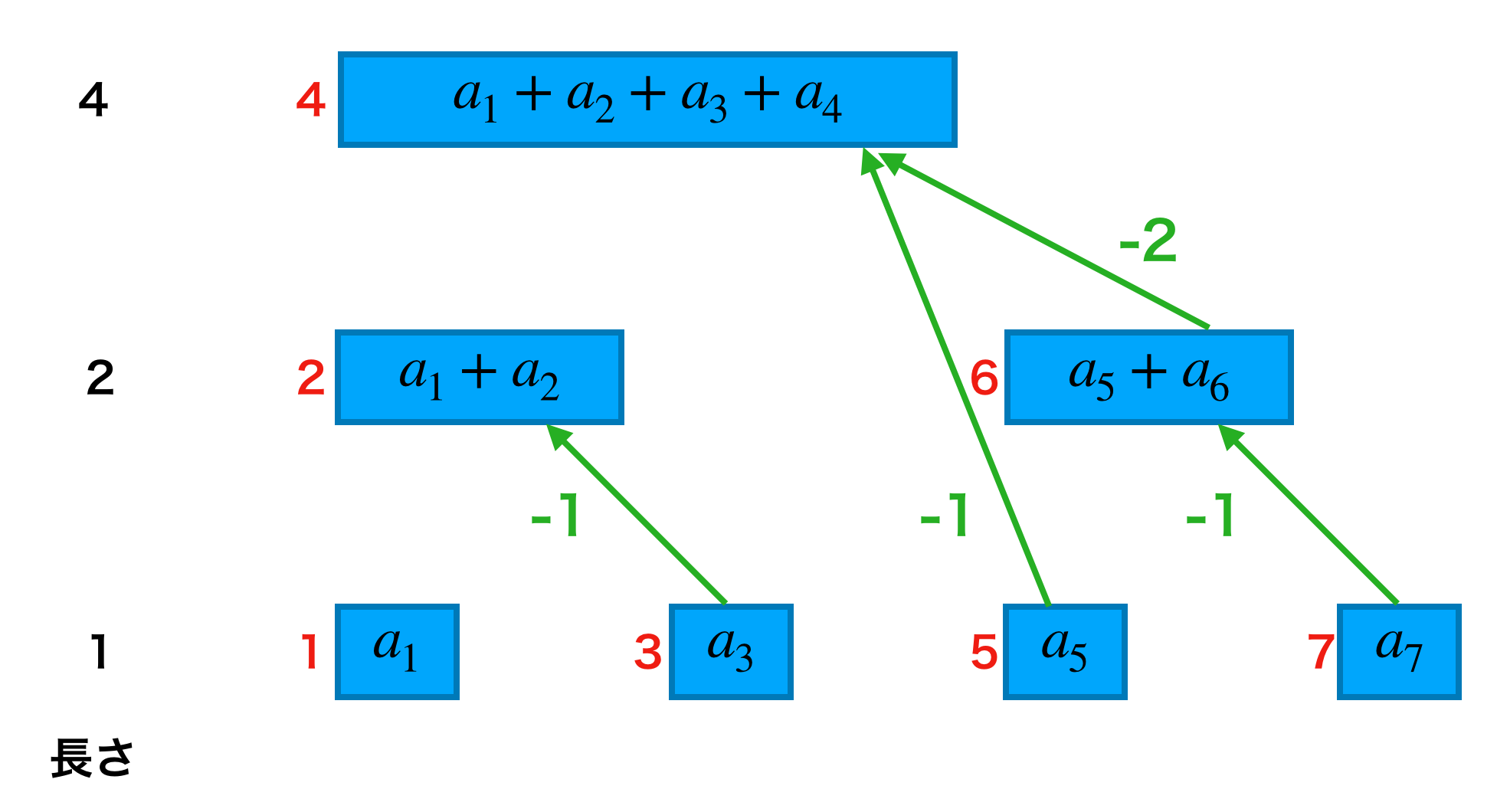
これだけだとなかなか法則性は見えてきませんね。ところが、「今いるインデックスと次にみたいインデックスの差分」に注目すると一気に見通しが良くなります。
赤字がdataのインデックスで緑矢印が道順、緑字がインデックスの差分を表します。この図を見ると下段からは +1、中段からは +2 をすれば良いことが分かります。この図の上段、中段、下段は「和をとる項の数」で分けられており、これを「長さ」と呼ぶことにします。例えば「data[6]の長さ」は 2 です。こうすると、クエリadd(i, x)を処理するためには以下のようにすれば良いと言えます。
インデックスを
i \leftarrow i + (data[i]の長さ)
と更新しつつ、data[i]に x を加算する。
3.2. クエリsum
つづいて、クエリsumをみていきます。クエリsum(i)は $a_1, \cdots, a_i$ を網羅するように辿り、それらの総和を取れば良いです。こちらも先ほどのクエリaddと同様に、「今いるインデックスと次にみたいインデックスの差分」に注目してみましょう。
やはり、「長さ」を使うことで次にみたいインデックスが分かります。したがって、クエリsum(i)を処理するためには以下のようにすれば良いと言えます。
インデックスを
i \leftarrow i - (data[i]の長さ)
と更新しつつ、各data[i]の総和をとる。
3.3. 長さ
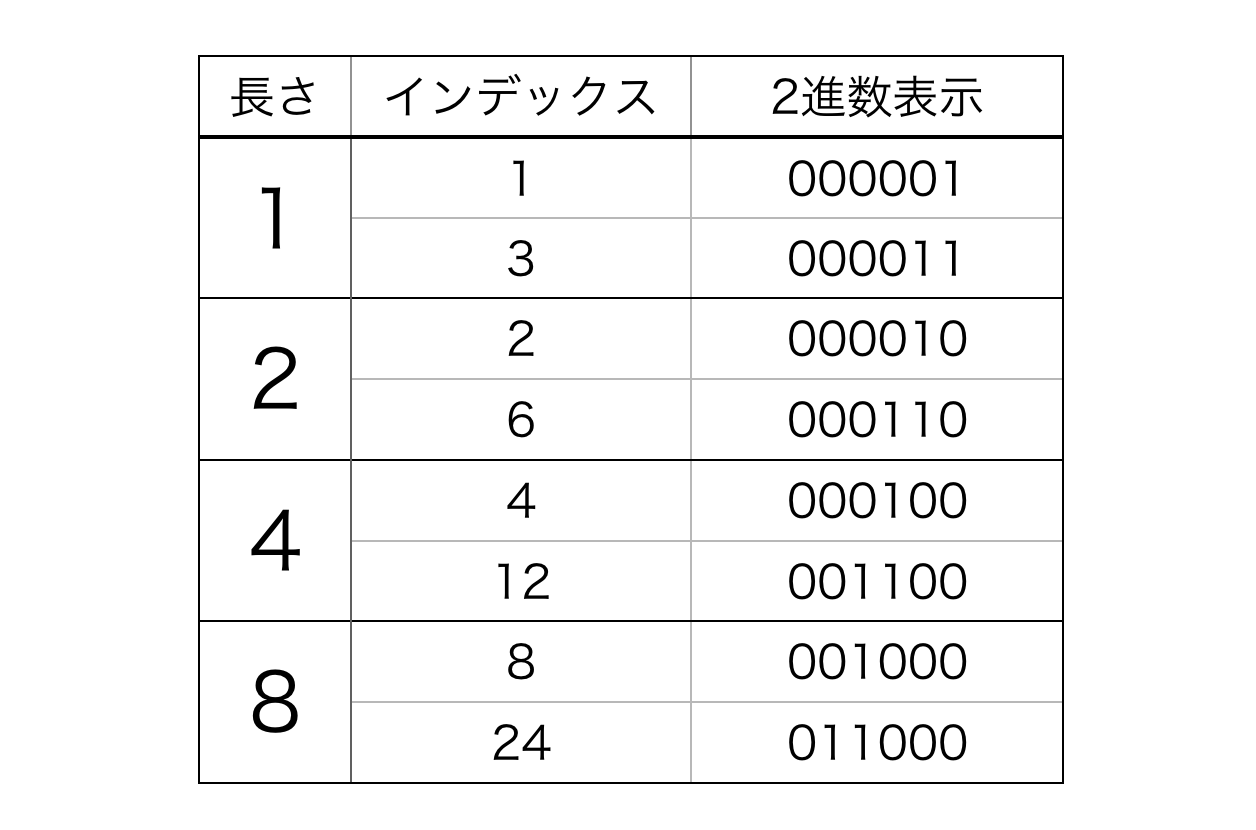
なんと、どちらのクエリも「data[i]の長さ」さえ得られれば処理できることが分かりました。では i からdata[i]の長さを得るにはどうすれば良いでしょうか。ここでフェニック木が Binary Indexed Tree とも呼ばれることを思い出しましょう。長さごとにインデックスとその2進数表示を示します。
この表から、長さは「インデックスを2進数表示し、右から見たときに初めて'1'が現れる場所」すなわち「'1'の最下位ビット」に対応していることが分かります。最下位ビットはよく英語で Least Significant Bit (LSB) と書かれます。
そして、「i における'1'のLSB」(= LSB(i)と書きます) はビット演算によって簡単に求めることができます。
LSB(i) \quad=\quad i\quad\&\quad(-i)
ここで&はビット毎のAND演算です。負の数に対するビット演算は、その数が2の補数表現で表されているとして処理されます(参考)。
いくつか例をみてみましょう。ここでは8ビットの2の補数表現で考えていきます。
$i = 6$ のとき
\begin{aligned}
LSB(6) &= 6 \quad\&\quad(-6)\\
&= (00000110)_2 \quad\&\quad (11111010)_2\\
&= (00000010)_2\\
&= 2
\end{aligned}
$i = 7$ のとき
\begin{aligned}
LSB(7) &= 7 \quad\&\quad(-7)\\
&= (00000111)_2 \quad\&\quad (11111001)_2\\
&= (00000001)_2\\
&= 1
\end{aligned}
$i = 24$ のとき
\begin{aligned}
LSB(24) &= 24 \quad\&\quad(-24)\\
&= (00011000)_2 \quad\&\quad (11101000)_2\\
&= (00001000)_2\\
&= 8
\end{aligned}
さあ、これでフェニック木を実装する準備が整いましたので実装していきましょう。
4. 実装
それでは実装していきます。変数名、メソッド名等はなるべくACLに沿って実装します。
4.1. コンストラクタ
クラスFenwick_Treeを作成しコンストラクタを実装します。
class Fenwick_Tree:
def __init__(self, n):
self._n = n # 要素数
self.data = [0] * n
要素数をインスタンス変数_nに保持し、長さ n のリストdataを作成します。初期化時点では全てが0です。これは数列$a = \{0,\cdots ,0\}$に対応します。0でない数列で初期化したい場合は各 i について$add(i, a_i)$を実行すれば良いです。
注意
前章までdataは1-indexedでしたが実装上は0-indexedとなります。フェニック木の仕組みは 1-indexed で成り立つので以降dataへのアクセスの際に1ずらす必要があることに注意してください。
4.2. add
まずメソッドaddから実装しましょう。このメソッドはクエリadd(p, x)に対応します。
def add(self, p, x):
assert 0 <= p < self._n
p += 1 # 0-indexed -> 1-indexed
while p <= self._n:
self.data[p - 1] += x # dataを更新
p += p & -p # pにLSB(p)を加算
3.1章でみたようにクエリaddではLSBを加算することで次に見るべきインデックスが分かります。このインデックスの更新とdataの更新を配列の参照外になるまで繰り返します。
4.3. sum
つづいてメソッドsumですが、ACLではクエリsum(i)に対応するものは内部の(privateな)関数として実装されており、実際に使用する外部の(publicな)関数はより汎用的なものが実装されています。具体的には、2つの値 l, r を指定することで左閉右開の半開区間 [l, r) の部分和
\sum_{i = l}^{r - 1}{a_i}
を返します。(aは0-indexed)
まず、クエリsumに対応する内部の関数から実装します。こちらは r に対して半開区間 [0, r)の部分和$a_0 + \cdots+ a_{r - 1}$を返します。ただし、$r = 0$のときは0を返します。また、内部の関数であることを表すために先頭にアンダースコア( _ )をつけました。
def _sum(self, r):
s = 0 # 総和を入れる変数
while r > 0:
s += self.data[r - 1]
r -= r & -r # rからLSB(r)を減算
return s
3.2章でみたようにクエリsumではLSBを減算することで次に見るべきインデックスが分かります。これを更新しつつ各data[r]の総和を取ります。
この内部関数を使って上で述べた汎用的な外部関数を実装します。
def sum(self, l, r):
assert 0 <= l <= r <= self._n
return self._sum(r) - self._sum(l)
([l, r) の部分和) = (r - 1 までの部分和) - (l - 1までの部分和)
です。
4.4. まとめ
以上をまとめるとこのようになります。
class Fenwick_Tree:
def __init__(self, n):
self._n = n
self.data = [0] * n
def add(self, p, x):
assert 0 <= p < self._n
p += 1
while p <= self._n:
self.data[p - 1] += x
p += p & -p
def sum(self, l, r):
assert 0 <= l <= r <= self._n
return self._sum(r) - self._sum(l)
def _sum(self, r):
s = 0
while r > 0:
s += self.data[r - 1]
r -= r & -r
return s
5. 使用例
本来は必要ないですが数列a自体を見るためにaに直接addを行なっています。
n = 8
a = [0, 1, 2, 3, 4, 5, 6, 7]
fw = Fenwick_Tree(n)
for i, a_i in enumerate(a): fw.add(i, a_i) # 数列aで初期化
print(fw.sum(2, 4)) # 5
print(fw.sum(6, 7)) # 6 sum(i, i + 1)でa[i]が得られる
fw.add(2, 6) # a[2] += 6
a[2] += 6
fw.add(5, -1) # a[5] += -1
a[5] += -1
print(a) # [0, 1, 8, 3, 4, 4, 6, 7]
print(fw.sum(0, 3)) # 9
print(fw.sum(3, 7)) # 17
6. 問題例
AtCoder Library Practice Contest B "Fenwick Tree"
7. おわりに
フェニック木の仕組みの解明からPythonでの実装までができました。フェニック木は応用が色々あるようなのでいずれ勉強してみたいです。
説明の間違いやバグ、アドバイス等ありましたらお知らせください。