0. はじめに
Pythonでべき乗・累乗を計算するには2つの方法があります。
例えば $3^4$ を計算する場合、
3 ** 4pow(3,4)
のどちらでも計算できます。1
本記事ではこれらの違いについて説明します。
内容は3章構成で以下の通りです。
第1章 **とpow()の違い
この章では主にPython初心者を対象に2つの方法の違いについて説明します。
第2章 速度の比較
この章では競技プログラミングなどの理由で計算速度を求める方を対象に2つの方法の実行時間を比較した結果を説明します。
第3章 Python内部のはなし
この章では第2章で見た結果の理由が知りたい方を対象にそれぞれの方法でPython内部で行われていることを説明します。
1. **とpow()の違い
この章ではPythonの基本事項を含め2つの方法の違いを説明します。
1.1. Python内での立場
1番の大きな違いはPython内での立場です。具体的にいうと
-
**は演算子 -
pow()は関数
です。
演算子は演算を行う指示で ** は「べき乗という演算をする」という意味があります。
+, %, !=, andなども全て演算子です。
関数は演算子などを用いて行う一連の処理をまとめたものです。pow()は「べき乗計算を行う」という関数なので以下のコードと一緒だと思っておけば良いでしょう。
def pow(a, b):
result = a ** b
return result
1.2. 第3の引数
少し発展的な内容となりますが、pow()関数には第3の引数があり、整数を指定することができます。
これを指定した場合、べき乗の結果を指定した整数で割ったあまりが得られます。指定しなかった場合はデフォルトでNoneが設定されているので前節で見た通りです。なお、第3の引数を指定する場合は第1、第2の引数も整数でなければなりません。
なのでpow()関数は実は以下のようなものです。2
def pow(a, b, c=None):
result = a ** b
if c is not None:
result = result % c # %はあまりを求める演算子
return result
1.3. まとめ
**とpow()は演算子と関数という違いがあります。
また、pow()は第3引数を指定することができ、指定した整数で割ったあまりを求めることができます。
このような違いがありますが、基本的にはどちらを使って書いても良いです。
例えば 「3の4乗を5で割ったあまり」は以下のように様々な書き方ができます。
# 以下のものは全て正しい答え(=1)が得られる
3 ** 4 % 5
pow(3, 4) % 5
pow(3, 4, 5)
ただし、2番目のようにわざわざ関数と演算子を混ぜる必要はないので1番目か3番目のように書くといいでしょう。
2. 速度の比較
この章では**とpow()の実行速度を比較します。
2.1. 計測方法
正整数 $x, n, m$ について
x ** npow(x, n)x ** n % mpow(x, n, m)
の4種類を計算しました。
実行時間の計測にはAtCoderのコードテスト Python(3.8.2)を使用し、各計算法について5回の計測の平均をとりました。
計測に使用したコードは以下のものです。
def main():
x = 3
n = 10
m = 17
loop = 10000000
for _ in range(loop):
result = x ** n
#result = pow(x, n)
#result = x ** n % m
#result = pow(x, n, m)
#pass
if __name__ == "__main__":
main()
2.2. 計測結果
結果は以下のようになりました。
$x=3, m = 17$ は固定で n と loop を変え計測しました。
なお、$loop = 10^7$ でfor文内がpassの場合は$196\rm{ms}$ でした。
(i)あまりをとらない場合
| n | loop | x ** n |
pow(x, n) |
|
|---|---|---|---|---|
| $10$ | $1$ | $21\rm{ms}$ | $22\rm{ms}$ | |
| $10$ | $10^7$ | $1885\rm{ms}$ | $2163\rm{ms}$ | |
| $10^7$ | $1$ | $2526\rm{ms}$ | $2516\rm{ms}$ | |
| $10^3$ | $2 \times10^6$ | $2311\rm{ms}$ | $2436\rm{ms}$ |
(ii)あまりをとる場合
| n | loop | x ** n % m |
pow(x, n, m) |
|
|---|---|---|---|---|
| $10$ | $1$ | $22\rm{ms}$ | $22\rm{ms}$ | |
| $10$ | $10^7$ | $2074\rm{ms}$ | $6319\rm{ms}$ | |
| $10^7$ | $1$ | $2553\rm{ms}$ | $25\rm{ms}$ | |
| $10^3$ | $2 \times10^6$ | $3652\rm{ms}$ | $1430\rm{ms}$ |
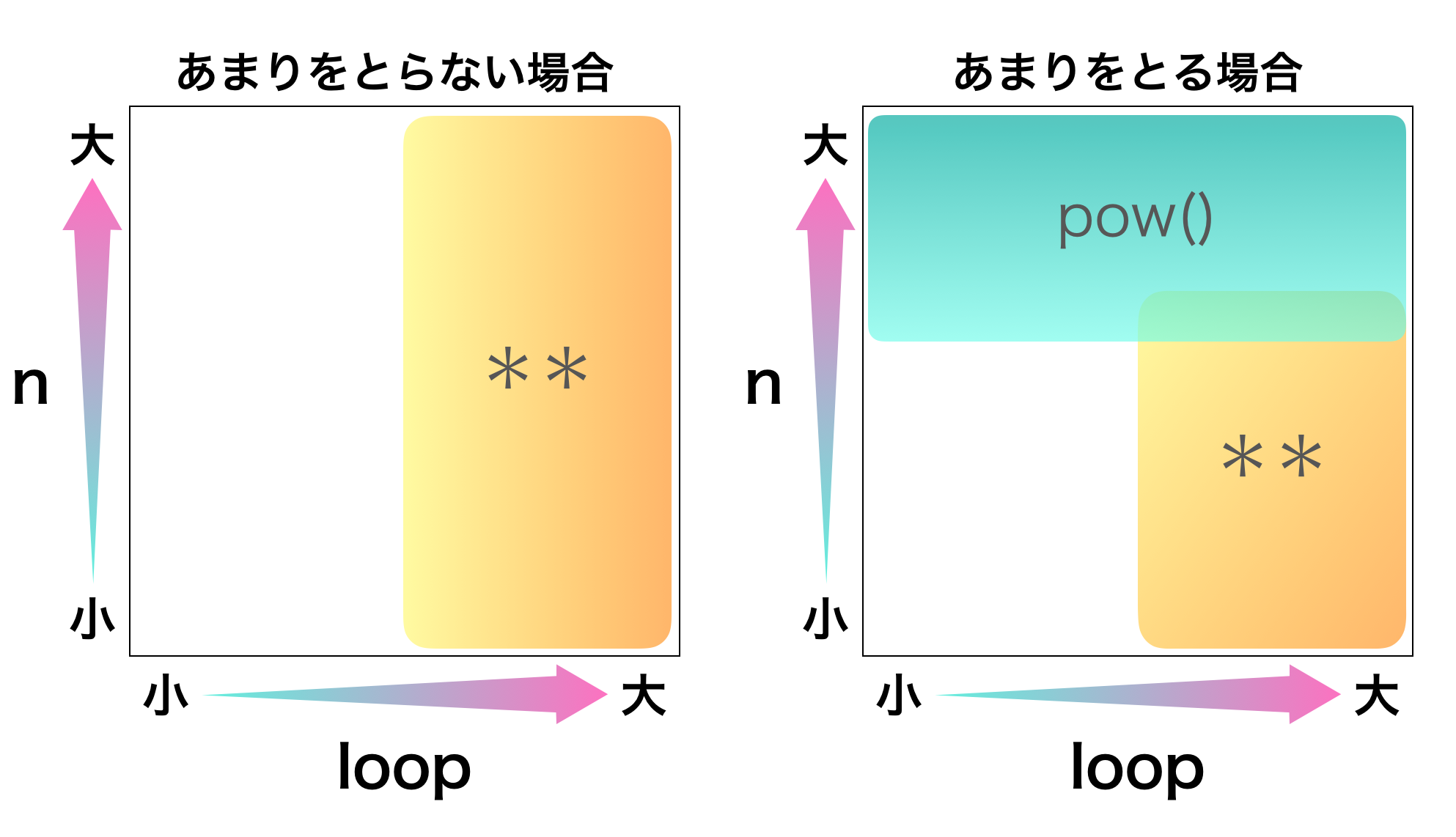
2.3. まとめ
結果をまとめると下図のようになります。
速度を重視したい場合に推奨する方法を示します。
空白部分はどちらでも大きな違いはありません。
当然ですが、べき乗計算にどちらの方法を使うか考えるよりもアルゴリズム自体を洗練させることに時間を使った方が良いです。べき乗計算の違いが重要になってくる場面は特定の場面(nが大きい & あまりをとる)を除いてほとんどないでしょう。
なのでこの結果はなんかちょっと違うらしいな程度にとどめて、実際はコードの統一性などで決めた方がいいと思います。
- n(正確には$x^n$)が大きい & あまりをとる $\rightarrow$
pow()を使う - その他 $\rightarrow$ コードの統一性などで決める
3. Python内部のはなし
競技プログラミングを始めて間もない頃、べき乗計算について調べてみると次のような文言をよく目にしました。
Pythonの組み込み関数pow()は繰り返し二乗法を用いて実装されている
当時は「ふーんそうなんだ、便利だな」としか思わなかったのですが、これを確かめたことはないなと思い調べてみたのがこの記事を書いたきっかけです。
この章では実際にPythonのソースコードをみて**とpow()の違いについて調べた結果を説明します。
なお、底、指数は整数のみを想定します。
参考にしたソースコード
オリジナルの、C言語で実装されたいわゆるCPythonで、バージョンは3.8です。以下のリンクからみることができます。
https://github.com/python/cpython/tree/3.8
3.1. 調べる方法
Python標準のdisモジュールを使います。このモジュールを使うことで、コードを実行した際に内部で行われている処理を人間がわかる形でみることができます。
例えば、以下のようなコードを書きます。
x = 1
y = 2
x + y
そして
$ python -m dis test.py
と実行すると
1 0 LOAD_CONST 0 (1)
2 STORE_NAME 0 (x)
2 4 LOAD_CONST 1 (2)
6 STORE_NAME 1 (y)
3 8 LOAD_NAME 0 (x)
10 LOAD_NAME 1 (y)
12 BINARY_ADD
14 POP_TOP
16 LOAD_CONST 2 (None)
18 RETURN_VALUE
このような結果が表示されると思います。
ここから、BINARY_ADDというのが足し算をしているようだということがわかります。
あとはソースコードからBINARY_ADDの定義を探して追っていけば内部での処理がわかります。
3.2. **の場合
以下のコードを使って調べました。
x = 3
y = 4
x ** y
すると以下のようになります。
1 0 LOAD_CONST 0 (3)
2 STORE_NAME 0 (x)
2 4 LOAD_CONST 1 (4)
6 STORE_NAME 1 (y)
3 8 LOAD_NAME 0 (x)
10 LOAD_NAME 1 (y)
12 BINARY_POWER
14 POP_TOP
16 LOAD_CONST 2 (None)
18 RETURN_VALUE
よってBINARY_POWERというものを探します。
これを追っていくと次のようになります。
BINARY_POWER $\rightarrow$ PyNumber_Power $\rightarrow$ ternary_op $\rightarrow$ long_pow
3.3. pow()の場合
以下のコードを使って調べました。
x = 3
y = 4
pow(x, y)
すると以下のようになります。
1 0 LOAD_CONST 0 (3)
2 STORE_NAME 0 (x)
2 4 LOAD_CONST 1 (4)
6 STORE_NAME 1 (y)
3 8 LOAD_NAME 2 (pow)
10 LOAD_NAME 0 (x)
12 LOAD_NAME 1 (y)
14 CALL_FUNCTION 2
16 POP_TOP
18 LOAD_CONST 2 (None)
20 RETURN_VALUE
pow()の場合はBINARY_POWERではなくCALL_FUNCTIONとなります。
これは、組み込み関数だけでなくコード中に自分で書いた関数など、全ての関数がCALL_FUNCTIONになります。
CALL_FUNCTIONからソースコードを追ってみると次のようになります。
CALL_FUNCTION $\rightarrow$ call_function $\rightarrow$ _PyObject_Vectorcall
そして_PyObject_Vectorcallのなかで以下のことが行われます。
\begin{aligned}
\rm{func} &= \rm{\_PyVectorcall\_Function}\\
&= \rm{builtin\_pow\_impl}\\
&= \rm{PyNumber\_Power}\\
&= \rm{ternary\_op}\\
&= \rm{\mathbf{long\_pow}}\\
\rm{result} &= \rm{func}()\\
&\rm{\_Py\_CheckFunctionResult}
\end{aligned}
3.4. long_pow
実はどちらの方法でべき乗計算をしようとしても結局long_powという関数にたどり着きます。
long_powをPythonで書いてみるとだいたい以下のようになります。(参照カウントや桁が大きい場合の処理などは省略しています。)
def long_pow(base, exp, mod): #base, exp, modはint
negativeOutput = 0
# 指数が負でmodがない場合はfloatの累乗へ移る
if exp < 0 and mod is None:
return float_pow(base, exp, mod)
# modが指定されている場合の処理
if mod != None:
#mod = 0はエラー
if mod == 0:
raise ValueError
#modが負ならnegativeOutputフラグを立ててmodを正にする
if mod < 0:
negativeOutput = 1
mod = -mod
# mod = 1なら必ず0
if mod == 1:
return 0
# 指数が負なら指数を正にして底をmodを法とした逆元で置き換える
if exp < 0:
exp = -exp
base = long_invmod(base, mod)
# 底が負もしくはmodより大きいならmodで割った余りに置き換える
if base < 0 or base > mod:
_, base = divmod(base, mod)
"""
ここまででmodが指定されている場合はbase, exp, modが非負になる。
modが指定されていない場合はbaseが負の場合もある。
"""
# modが指定されている場合、xをmodで割った余りに置き換える
def REDUCE(x):
if mod != None:
_, x = divmod(x, mod)
return x
# xとyの掛け算。modが指定されている場合はあまりをとる
def MULT(x, y):
result = x * y
result = REDUCE(result)
return result
# 右向きバイナリ法(繰り返し二乗法)
j = 1 << exp.bit_length() - 1
z = 1
while j:
z = MULT(z, z)
if exp & j:
z = MULT(z, base)
j >>= 1
# negativeOutputの場合は結果を負にする
if negativeOutput and z != 0:
z -= mod
return z
以上より「Pythonの組み込み関数pow()は繰り返し二乗法を用いて実装されている」という文言は正しいですが誤解を含んでいると思います。(私が勝手に誤解していただけかもしれません。)
正しい
確かに組み込み関数pow()は繰り返し二乗法を用いて実装されています。
誤解(?)
pow() ""は"" 繰り返し二乗法を~ということは**は違う?
$\rightarrow$ **も繰り返し二乗法を用いて実装されています。
そもそも、どちらも同じ関数を使っています。
以降では、ここまででわかったことを基に2章の結果を説明します。
3.5. あまりをとらない場合
まず、あまりをとらない場合を見ていきます。
この場合どちらもlong_pow(x, n, None)が実行されるだけなので
x ** npow(x, n)
はアルゴリズムの面では完全に等しいです。したがって、$n$ がどのような大きさであっても2つに違いはありません。
1章で述べた通り、**は演算子、pow()は関数です。ここではこの違いが重要になります。
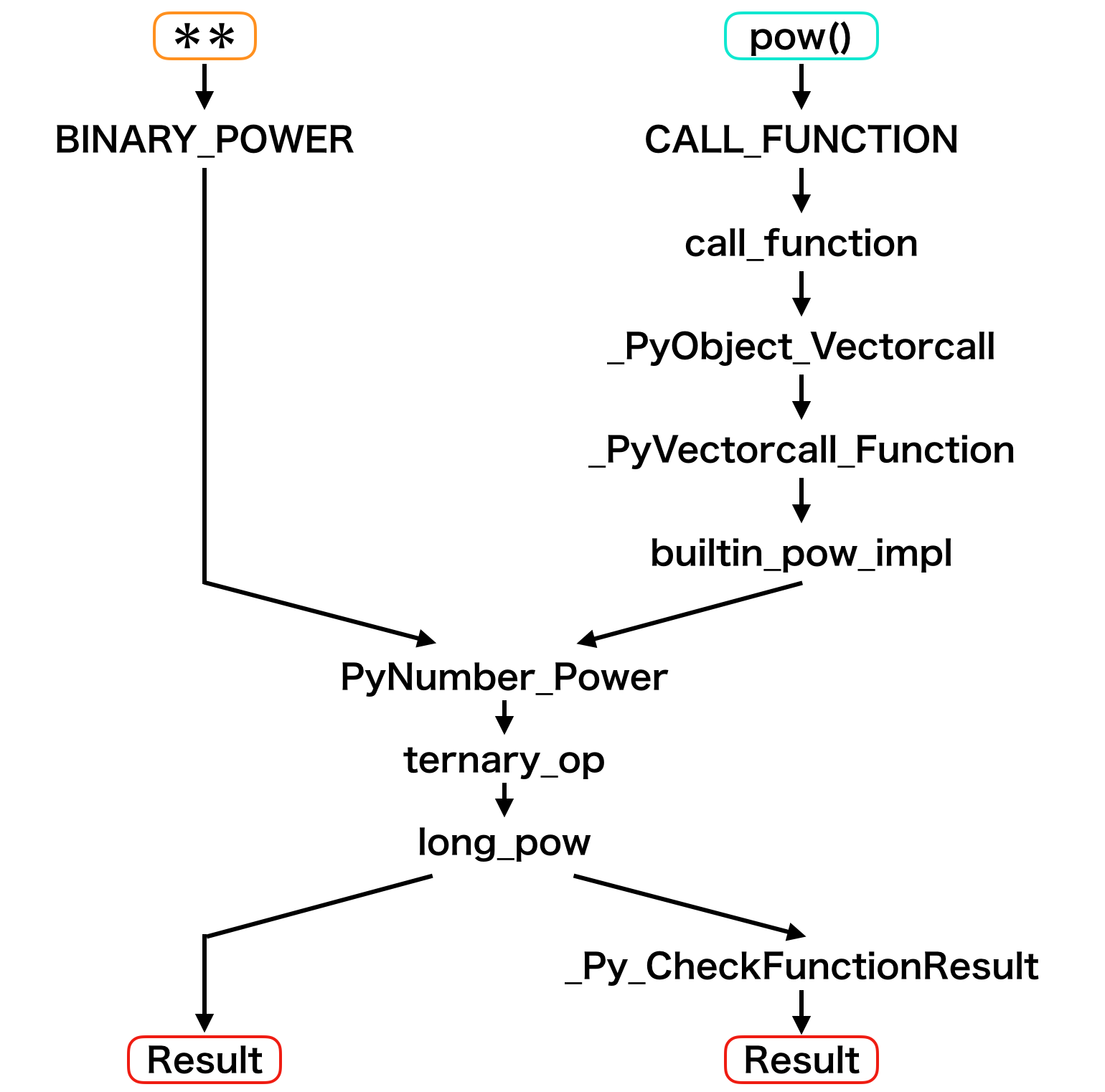
ここで3.2, 3.3でわかったPython内部の動きをまとめてみると下図のようになります。
この図からわかるように、関数を呼び出す際にはコスト(関数呼び出しのオーバーヘッド)を支払うことになります。
1回の呼び出しでは体感できる差は生まれませんが、呼び出し回数が増えれば大きな差になります。
このような理由から、
- n の大きさに依存しない
- loopが大きくなるほど演算子である
**が関数であるpow()より速度面で優位になる
という2章の結果を説明できます。
3.6. あまりをとる場合
続いて、あまりをとる場合を見ていきます。
この場合も演算子と関数の違いからloopの大きさによって演算子の優位性が見えてきます。
一方、あまりをとらない場合と違うのはアルゴリズムの面でも2つは異なるという部分です。
x ** n % mではあまりを求めるのは最後だけなのに対し、pow(x, n, m)は乗算ごとにあまりを求めます。ここからはこれらの違いが n の大きさによってどのように影響するかを見ていきます。
n が小さい場合
この場合、「割り算のコストは小さくない」という事実が重要になってきます。あまりを求めるというのは割り算をすることに他ならないので何度もあまりを求めるpow(x, n, m)は一度しかあまりを求めないx ** n % mに比べて計算コストが大きくなります。
n が大きい場合
この場合、「大きな数の掛け算のコストが無視できない」という事実が重要になります。$x^n$ は指数関数ですので n が大きくなると $x^n$ は非常に大きくなります。そのため、一時的に $x^n$ そのものを求めるx ** n % mは常に m 未満の数の掛け算をするpow(x, n, m)に比べて計算コストが大きくなります。
これらをまとめると
- n が小さく loop が大きい場合は割り算と関数呼び出しのコストが支配的になり
pow()の方が**より遅くなる - n が大きく loop が小さい場合は大きな数の掛け算のコストが支配的になり
**の方がpow()より遅くなる - n と loop が共に大きい場合はこれらのせめぎ合いになるが、$x^n$ が指数関数だということをふまえると概ね
**の方がpow()より遅くなる
というように2章の結果を説明できます。
3.7. まとめ
**とpow()は共にlong_powという関数につながっていて、long_powは繰り返し二乗法を用いて実装されています。
**とpow()の実行速度を比較するポイントは
- あまりをとらない場合は「関数呼び出しのオーバーヘッド」
- あまりをとる場合は加えて「割り算」と「大きな数の掛け算」
でこれらのコストのうちどれが支配的になるかを考えることによって判断できます。
4. おわりに
実用性はあまりなさそうな内容ですが、Pythonについて理解が深まったのでよかったです。
説明の間違いやバグ等ありましたらお知らせください。