LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@RYA234(RYA234)

JavaScriptで蟻本 グラフ ダイクストラ法

Last updated at Posted at 2024-10-08

概要

アルゴリズムの学習記録を投稿します。
今回は蟻本・グラフのダイクストラ法　p96 についてです。
隣接行列を使った方法です。

問題

以下隣接行列の点A-点G間の最短距離を求めなさい。

[
[0,2,5,INF,INF,INF,INF],
[2,0,4,6,10,INF,INF],
[5,4,0,2,INF,INF,INF],
[INF,6,2,0,INF,1,INF],
[INF,10,INF,0,INF,3,5],
[INF,INF,INF,1,3,0,9],
[INF,INF,INF,INF,5,9,0]
]

出力
16

コード部分

    //
    /** p97 隣接行列を使った配列ダイクストラ法
     * @param destination{Number}  目的値の番号
     * @param vertexCount{Number}  頂点の数
     * @param edgeCount{Number}  辺の数
     * @return {Number} 最短経路のコスト
     */
    const  cal= (destination,vertexCount,edge,goal) =>{
        const INF = 1000;

        let isUsed = Array(vertexCount).fill(false);
        let minDistance = Array(vertexCount).fill(INF);
        minDistance[destination] = 0;
        console.log(`u|v|行動 or 条件 | 結果|minDistance`)
        console.log(`-------|-|------------------------|---------|------|`)

        while(true){
            let v = -1;
            // まだ使用されてない頂点のうち、最小のものを探す。
            for(let u=0; u<vertexCount; u++){
                if(!isUsed[u] && (v == -1 || minDistance[u] < minDistance[v])) {
                      console.log(`${u}|${v}|頂点${u}が使用されていないかつ最小 </br> !isUsed[u]（!${!isUsed[u]}） minDistance[u]（${minDistance[u]}） < minDistance[v]（${minDistance[v]}） | v = u（${u})|${minDistance}`)
                    v = u;
                }
            }
            // 最小の者が見つからない場合は終了
            if(v == -1)break;

            isUsed[v] = true;
            // vから行ける頂点に対して、最小のコストを更新する。
            for(let u = 0; u< vertexCount; u++){
                console.log(`${u}|${v}|頂点${v}から行ける頂点に対して、最小のコストを更新する。 </br> minDistance[u]（${u}）, minDistance[v]（${v}） + edge[v][u]</br> ${minDistance[u]}, ${minDistance[v]}+${edge[v][u]}  | minDistance[u]（${u}）=${Math.min(minDistance[u], minDistance[v] + edge[v][u])} |${minDistance}`)
            }
        }
        console.log(minDistance);
        return minDistance[goal];
    }
    
    const INF = 1000;
  let edge1 = [
              [0,2,5,INF,INF,INF,INF],
              [2,0,4,6,10,INF,INF],
              [5,4,0,2,INF,INF,INF],
              [INF,6,2,0,INF,1,INF],
              [INF,10,INF,0,INF,3,5],
              [INF,INF,INF,1,3,0,9],
              [INF,INF,INF,INF,5,9,0]
            ]
    // 結果値は16
    console.log(cal(0,7,edge1,6))

python tutor

コードを実際に動かせるwebサイト
ステップ実行かつステップ事の変数を確認できる特徴があります。

Python Tutorリンク

その他情報

感想

処理の流れはなんとなく把握できたぐらいです。
まだまだ理解足りないですね。難しい

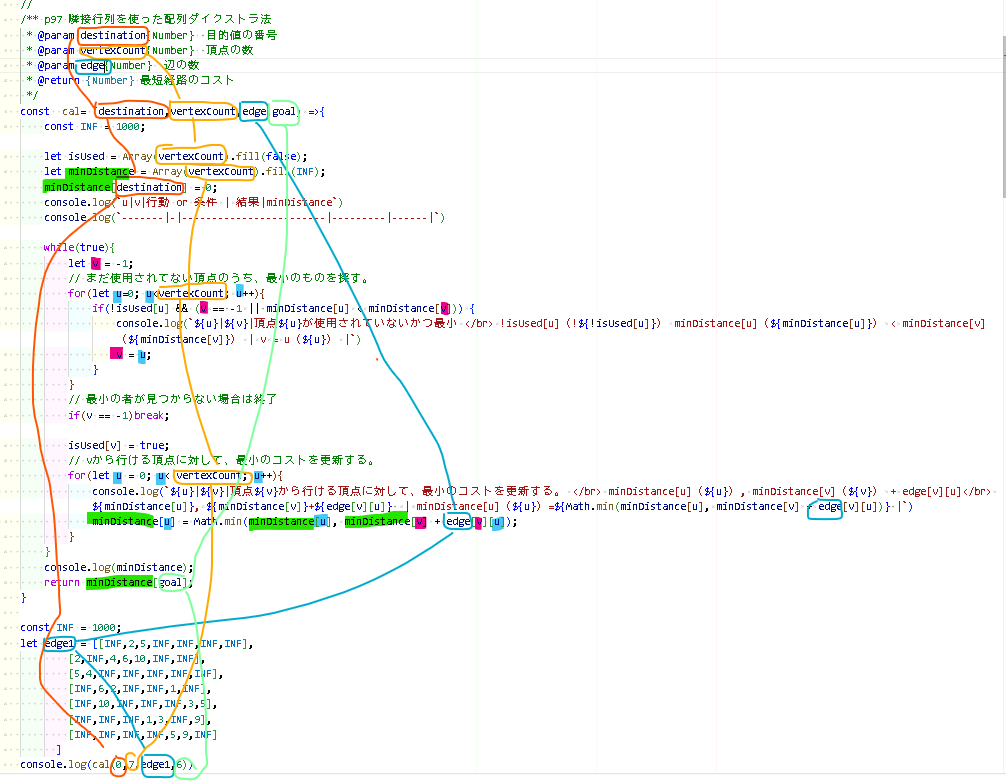
依存関係グラフ

依存関係グラフは変数の結びつきを一目でわかりやすくするための図です。
変数の流れを確認しやすくすることでワーキングメモリの負担を減らすことができます。
作成方法はコード上の変数に丸付けて線を繋げています。

image.png

状態遷移図

計算内容を明示する表。
ステップごとの変数の値を各列に表示します。
複雑な計算を行うコードを理解するのに役立つ表です。

u v 行動 or 条件 結果 minDistance
0 -1 頂点0が使用されていないかつ最小 !isUsed[u]（!true） minDistance[u]（0） < minDistance[v]（undefined） v = u（0) 0,1000,1000,1000,1000,1000,1000
0 0 頂点0から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（0）, minDistance[v]（0） + edge[v][u] 0, 0+0 minDistance[u]（0）=0 0,1000,1000,1000,1000,1000,1000
1 0 頂点0から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（1）, minDistance[v]（0） + edge[v][u] 1000, 0+2 minDistance[u]（1）=2 0,1000,1000,1000,1000,1000,1000
2 0 頂点0から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（2）, minDistance[v]（0） + edge[v][u] 1000, 0+5 minDistance[u]（2）=5 0,2,1000,1000,1000,1000,1000
3 0 頂点0から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（3）, minDistance[v]（0） + edge[v][u] 1000, 0+1000 minDistance[u]（3）=1000 0,2,5,1000,1000,1000,1000
4 0 頂点0から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（4）, minDistance[v]（0） + edge[v][u] 1000, 0+1000 minDistance[u]（4）=1000 0,2,5,1000,1000,1000,1000
5 0 頂点0から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（5）, minDistance[v]（0） + edge[v][u] 1000, 0+1000 minDistance[u]（5）=1000 0,2,5,1000,1000,1000,1000
6 0 頂点0から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（6）, minDistance[v]（0） + edge[v][u] 1000, 0+1000 minDistance[u]（6）=1000 0,2,5,1000,1000,1000,1000
1 -1 頂点1が使用されていないかつ最小 !isUsed[u]（!true） minDistance[u]（2） < minDistance[v]（undefined） v = u（1) 0,2,5,1000,1000,1000,1000
0 1 頂点1から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（0）, minDistance[v]（1） + edge[v][u] 0, 2+2 minDistance[u]（0）=0 0,2,5,1000,1000,1000,1000
1 1 頂点1から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（1）, minDistance[v]（1） + edge[v][u] 2, 2+0 minDistance[u]（1）=2 0,2,5,1000,1000,1000,1000
2 1 頂点1から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（2）, minDistance[v]（1） + edge[v][u] 5, 2+4 minDistance[u]（2）=5 0,2,5,1000,1000,1000,1000
3 1 頂点1から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（3）, minDistance[v]（1） + edge[v][u] 1000, 2+6 minDistance[u]（3）=8 0,2,5,1000,1000,1000,1000
4 1 頂点1から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（4）, minDistance[v]（1） + edge[v][u] 1000, 2+10 minDistance[u]（4）=12 0,2,5,8,1000,1000,1000
5 1 頂点1から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（5）, minDistance[v]（1） + edge[v][u] 1000, 2+1000 minDistance[u]（5）=1000 0,2,5,8,12,1000,1000
6 1 頂点1から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（6）, minDistance[v]（1） + edge[v][u] 1000, 2+1000 minDistance[u]（6）=1000 0,2,5,8,12,1000,1000
2 -1 頂点2が使用されていないかつ最小 !isUsed[u]（!true） minDistance[u]（5） < minDistance[v]（undefined） v = u（2) 0,2,5,8,12,1000,1000
0 2 頂点2から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（0）, minDistance[v]（2） + edge[v][u] 0, 5+5 minDistance[u]（0）=0 0,2,5,8,12,1000,1000
1 2 頂点2から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（1）, minDistance[v]（2） + edge[v][u] 2, 5+4 minDistance[u]（1）=2 0,2,5,8,12,1000,1000
2 2 頂点2から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（2）, minDistance[v]（2） + edge[v][u] 5, 5+0 minDistance[u]（2）=5 0,2,5,8,12,1000,1000
3 2 頂点2から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（3）, minDistance[v]（2） + edge[v][u] 8, 5+2 minDistance[u]（3）=7 0,2,5,8,12,1000,1000
4 2 頂点2から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（4）, minDistance[v]（2） + edge[v][u] 12, 5+1000 minDistance[u]（4）=12 0,2,5,7,12,1000,1000
5 2 頂点2から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（5）, minDistance[v]（2） + edge[v][u] 1000, 5+1000 minDistance[u]（5）=1000 0,2,5,7,12,1000,1000
6 2 頂点2から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（6）, minDistance[v]（2） + edge[v][u] 1000, 5+1000 minDistance[u]（6）=1000 0,2,5,7,12,1000,1000
3 -1 頂点3が使用されていないかつ最小 !isUsed[u]（!true） minDistance[u]（7） < minDistance[v]（undefined） v = u（3) 0,2,5,7,12,1000,1000
0 3 頂点3から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（0）, minDistance[v]（3） + edge[v][u] 0, 7+1000 minDistance[u]（0）=0 0,2,5,7,12,1000,1000
1 3 頂点3から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（1）, minDistance[v]（3） + edge[v][u] 2, 7+6 minDistance[u]（1）=2 0,2,5,7,12,1000,1000
2 3 頂点3から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（2）, minDistance[v]（3） + edge[v][u] 5, 7+2 minDistance[u]（2）=5 0,2,5,7,12,1000,1000
3 3 頂点3から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（3）, minDistance[v]（3） + edge[v][u] 7, 7+0 minDistance[u]（3）=7 0,2,5,7,12,1000,1000
4 3 頂点3から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（4）, minDistance[v]（3） + edge[v][u] 12, 7+1000 minDistance[u]（4）=12 0,2,5,7,12,1000,1000
5 3 頂点3から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（5）, minDistance[v]（3） + edge[v][u] 1000, 7+1 minDistance[u]（5）=8 0,2,5,7,12,1000,1000
6 3 頂点3から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（6）, minDistance[v]（3） + edge[v][u] 1000, 7+1000 minDistance[u]（6）=1000 0,2,5,7,12,8,1000
4 -1 頂点4が使用されていないかつ最小 !isUsed[u]（!true） minDistance[u]（12） < minDistance[v]（undefined） v = u（4) 0,2,5,7,12,8,1000
5 4 頂点5が使用されていないかつ最小 !isUsed[u]（!true） minDistance[u]（8） < minDistance[v]（12） v = u（5) 0,2,5,7,12,8,1000
0 5 頂点5から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（0）, minDistance[v]（5） + edge[v][u] 0, 8+1000 minDistance[u]（0）=0 0,2,5,7,12,8,1000
1 5 頂点5から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（1）, minDistance[v]（5） + edge[v][u] 2, 8+1000 minDistance[u]（1）=2 0,2,5,7,12,8,1000
2 5 頂点5から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（2）, minDistance[v]（5） + edge[v][u] 5, 8+1000 minDistance[u]（2）=5 0,2,5,7,12,8,1000
3 5 頂点5から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（3）, minDistance[v]（5） + edge[v][u] 7, 8+1 minDistance[u]（3）=7 0,2,5,7,12,8,1000
4 5 頂点5から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（4）, minDistance[v]（5） + edge[v][u] 12, 8+3 minDistance[u]（4）=11 0,2,5,7,12,8,1000
5 5 頂点5から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（5）, minDistance[v]（5） + edge[v][u] 8, 8+0 minDistance[u]（5）=8 0,2,5,7,11,8,1000
6 5 頂点5から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（6）, minDistance[v]（5） + edge[v][u] 1000, 8+9 minDistance[u]（6）=17 0,2,5,7,11,8,1000
4 -1 頂点4が使用されていないかつ最小 !isUsed[u]（!true） minDistance[u]（11） < minDistance[v]（undefined） v = u（4) 0,2,5,7,11,8,17
0 4 頂点4から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（0）, minDistance[v]（4） + edge[v][u] 0, 11+1000 minDistance[u]（0）=0 0,2,5,7,11,8,17
1 4 頂点4から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（1）, minDistance[v]（4） + edge[v][u] 2, 11+10 minDistance[u]（1）=2 0,2,5,7,11,8,17
2 4 頂点4から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（2）, minDistance[v]（4） + edge[v][u] 5, 11+1000 minDistance[u]（2）=5 0,2,5,7,11,8,17
3 4 頂点4から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（3）, minDistance[v]（4） + edge[v][u] 7, 11+0 minDistance[u]（3）=7 0,2,5,7,11,8,17
4 4 頂点4から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（4）, minDistance[v]（4） + edge[v][u] 11, 11+1000 minDistance[u]（4）=11 0,2,5,7,11,8,17
5 4 頂点4から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（5）, minDistance[v]（4） + edge[v][u] 8, 11+3 minDistance[u]（5）=8 0,2,5,7,11,8,17
6 4 頂点4から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（6）, minDistance[v]（4） + edge[v][u] 17, 11+5 minDistance[u]（6）=16 0,2,5,7,11,8,17
6 -1 頂点6が使用されていないかつ最小 !isUsed[u]（!true） minDistance[u]（16） < minDistance[v]（undefined） v = u（6) 0,2,5,7,11,8,16
0 6 頂点6から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（0）, minDistance[v]（6） + edge[v][u] 0, 16+1000 minDistance[u]（0）=0 0,2,5,7,11,8,16
1 6 頂点6から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（1）, minDistance[v]（6） + edge[v][u] 2, 16+1000 minDistance[u]（1）=2 0,2,5,7,11,8,16
2 6 頂点6から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（2）, minDistance[v]（6） + edge[v][u] 5, 16+1000 minDistance[u]（2）=5 0,2,5,7,11,8,16
3 6 頂点6から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（3）, minDistance[v]（6） + edge[v][u] 7, 16+1000 minDistance[u]（3）=7 0,2,5,7,11,8,16
4 6 頂点6から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（4）, minDistance[v]（6） + edge[v][u] 11, 16+5 minDistance[u]（4）=11 0,2,5,7,11,8,16
5 6 頂点6から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（5）, minDistance[v]（6） + edge[v][u] 8, 16+9 minDistance[u]（5）=8 0,2,5,7,11,8,16
6 6 頂点6から行ける頂点に対して、最小のコストを更新する。 minDistance[u]（6）, minDistance[v]（6） + edge[v][u] 16, 16+0 minDistance[u]（6）=16 0,2,5,7,11,8,16

参考資料

プログラミングコンテストチャレンジブック [第2版]　マイナビ　p96

プログラマー脳　秀和システム
p73 python tutor
p71 状態遷移表　
p69 依存関係グラフ

githubコミット部分

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?