scipy.stats.truncnorm.rvs の高速化

scipy.stats.truncnorm.rvs の高速化

切断正規分布に従う逆関数法を用いた乱数生成を自前で実装したら scipy.stats.truncnorm.rvs よりだいぶ速かった話.
後述するがバージョンに強く依存して SciPy 1.9 で大幅に緩和されている.

import numpy as np
from scipy.stats import truncnorm
rng = np.random.default_rng()

from scipy.special import erf, erfinv
import matplotlib.pyplot as plt

import scipy.version
print('numpy', np.version.full_version)
print('scipy', scipy.version.full_version)

numpy 1.21.5
scipy 1.7.3

scipy.stats による切断正規分布 (の乱数生成)

cf. 切断正規分布 - NtRand

SciPy には scipy.stats に各種確率分布を扱うクラスが実装されていて, scipy.stats.truncnorm クラスで切断正規分布を扱える.
乱数生成は scipy.stats.hogehoge.rvs で行う.

切断正規分布のパラメータは 下限, 上限, 平均, 標準偏差の4つ.
scipy.stats.truncnorm で扱う場合, 下限, 上限は標準化した状態で考えて, 平均, 標準偏差は切断しない状態の正規分布のものを与える.
実際の下 (上) 限は,

平均+標準偏差*下 (上) 限

で算出される.
実際の平均, 標準偏差は後述の誤差関数を使って計算することができ, パラメータとしての平均, 標準偏差とは異なる値になるので注意.
具体的な式は上で挙げたサイト等を参照.

scipy.stats.truncnorm (及びその他の確率分布クラス) にはパラメータを配列で渡せて, 異なるパラメータ毎の乱数生成を一行で書ける.
乱数生成器に numpy.random.Generator を使いたいなら scipy.stats.truncnorm.rvs の random_state オプションに渡す.

# データパラメータ # サンプル数, 次元
n = 10**3
d = 5*10**2

# truncnorm のパラメータ
# 適当に成分毎に乱数で設定
stdmin = rng.uniform(-2, -1, size=d)
stdmax = rng.uniform(1, 2, size=d)
mean = rng.normal(size=d)
std = np.exp(rng.normal(size=d))

# サンプリング & 時間計測 & 比較
%time truncnorm.rvs(stdmin, stdmax, mean, std, size=[n, d], random_state=rng)
%time rng.normal(mean, std, size=[n, d])

Wall time: 64.5 ms
Wall time: 12.1 ms

500 次元 1000 サンプルずつで切断正規分布が正規分布の5倍程度の時間.
確率分布が少し複雑だからこんなもんかという感じもする.

ところがサンプル数/次元のバランスを変えてみると...

# サンプル数, 次元を調整
n = 10**0
d = 5*10**5

stdmin = rng.uniform(-2, -1, size=d)
stdmax = rng.uniform(1, 2, size=d)
mean = rng.normal(size=d)
std = np.exp(rng.normal(size=d))

%time truncnorm.rvs(stdmin, stdmax, mean, std, size=[n, d], random_state=rng)
%time rng.normal(mean, std, size=[n, d])

Wall time: 40.3 s
Wall time: 15.8 ms

numpy.random.Generator を使った正規分布の乱数が数 ms 増で誤差の範囲なのに対して scipy.stats.truncnorm.rvs による切断正規分布の乱数は 1000 倍弱.
確率分布が少し複雑だからとはいえさすがに...な遅さ.
精査してないけど次元 1000 倍で実行時間約 1000 倍なのとソースにパラメータ配列について while 文を回してるっぽいところがあるのでここに原因がありそう.
cf. https://github.com/scipy/scipy/blob/38cd478334a07b6e9dfe224a3ff66ad356c53524/scipy/stats/_continuous_distns.py#L8251

逆関数法による切断正規分布の乱数生成

SciPy は NumPy を使った科学技術計算ライブラリなので, NumPy と条件を合わせてるのに SciPy だけ実行速度が大きく変わるのはちょっと気持ち悪い.
というわけで切断正規分布の乱数生成関数を自前で実装してみる.

一般の確率分布に従う乱数の生成方法の 1 つに逆関数法がある.
逆関数法自体の解説は他に任せるが, 切断正規分布の場合も逆関数法による乱数生成法が知られている.
一様分布に従うサンプル $Z$ と正規分布の累積分布関数 $\Phi$ によって,

$$ X_\mathrm{std} = \Phi^{-1}((\Phi(b)-\Phi(a))Z+\Phi(a)), $$

と変換すると下限 $a$, 上限 $b$ の切断標準正規分布 (標準正規分布 $\mathcal{N}(0, 1)$ を $[a, b]$ で切断した分布) に従うサンプル $X_\mathrm{std}$ が生成され, これを $\sigma$ 倍して $\mu$ を足すことで平均パラメータ $\mu$, 標準偏差パラメータ $\sigma$ の切断標準正規分布に従う乱数が得られる.

正規分布の累積分布関数には SciPy 等に実装されている誤差関数を使うといい.
cf, 誤差関数と正規分布-01
$\Phi$ は誤差関数 $\mathrm{erf}$ を使って,

$$ \Phi(x) = \frac{1}{2}\left(1+\mathrm{erf}\left(\frac{x}{\sqrt{2}}\right)\right), $$

と書けて, 上の式に代入して整理すると,

$$ X_\mathrm{std} = \sqrt{2}\mathrm{erf}^{-1}\left(\left(\mathrm{erf}\left(\frac{b}{\sqrt{2}}\right)-\mathrm{erf}\left(\frac{a}{\sqrt{2}}\right)\right)Z+\mathrm{erf}\left(\frac{a}{\sqrt{2}}\right)\right), $$

と書き直される.
SciPy での誤差関数とその逆関数はそれぞれ scipy.special.erf, scipy.special.erfinv.

n = 10**0
d = 5*10**5

stdmin = rng.uniform(-2, -1, size=d)
stdmax = rng.uniform(1, 2, size=d)
mean = rng.normal(size=d)
std = np.exp(rng.normal(size=d))

def truncnorm_rvs(stdmin, stdmax, mean, std, size):
    # 1. 一様分布に従ってサンプリング
    Z = rng.uniform(size=size)
    # 2. erf, erfinv を使って標準切断正規分布に従うサンプルに変換
    emin = erf(stdmin/np.sqrt(2))
    emax = erf(stdmax/np.sqrt(2))
    Xstd = np.sqrt(2)*erfinv((emax-emin)*Z+emin)
    # 3. mean と std で目的の平均, 標準偏差に変換
    return mean+std*Xstd

%time truncnorm_rvs(stdmin, stdmax, mean, std, size=[n, d])

Wall time: 55.7 ms

はっや.
さすがに numpy.random.Generator による正規分布よりは遅いが 500 次元 1000 サンプルの scipy.stats.truncnorm.rvs より速くなるとは思ってなかった.

検算 (目視)

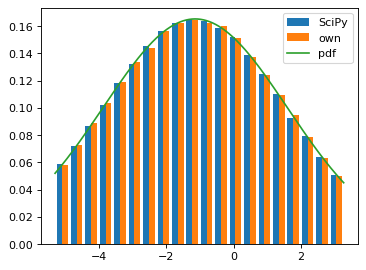
念のためちゃんと目的の切断正規分布に従うサンプルになっているかヒストグラムで目視検算¹してみる².
scipy.stats.truncnorm.rvs によるサンプル, 自前実装によるサンプル, 確率密度関数のグラフを重ねて描画.
ヒストグラムは matplotlib.pyplot.hist にオプションで density=True とすれば確率密度関数とスケールを合わせられる.

# パラメータ, サンプル生成
n = 5*10**5
stdmin = rng.uniform(-1, 0)-1
stdmax = rng.uniform(0, 1)+1
mean = rng.normal()
std = np.exp(rng.normal())
x_sp = truncnorm.rvs(stdmin, stdmax, mean, std, size=n, random_state=rng)
x_my = truncnorm_rvs(stdmin, stdmax, mean, std, size=n)

# 確率密度関数グラフのデータ生成
a = mean+std*stdmin
b = mean+std*stdmax
t = np.linspace(a, b, 1000)
emin = erf(stdmin/np.sqrt(2))
emax = erf(stdmax/np.sqrt(2))
Z = 0.5*(emax-emin)
y = 1/np.sqrt(2*np.pi)/std*np.exp(-0.5*np.square((t-mean)/std))/Z

# 描画
bins = 20
plt.hist([x_sp, x_my], bins=bins, density=True, label=['SciPy', 'own'])
plt.plot(t, y, label='pdf')
plt.show()

完全に一致.

SciPy 1.9.3 の場合

探したら GitHub に Issue が上がっていて SciPy 1.9 で修正されたとのこと.
cf. truncnorm.rvs is painfully slow on version 1.5.0rc2 · Issue #12370 · scipy/scipy · GitHub
手元に SciPy 1.9.3 の環境もあったので試してみた.

import numpy as np
from scipy.stats import truncnorm
from scipy.special import erf, erfinv
rng = np.random.default_rng()

def truncnorm_rvs(stdmin, stdmax, mean, std, size):
    Z = rng.uniform(size=size)
    emin = erf(stdmin/np.sqrt(2))
    emax = erf(stdmax/np.sqrt(2))
    Xstd = np.sqrt(2)*erfinv((emax-emin)*Z+emin)
    return mean+std*Xstd

import scipy.version
print('numpy', np.version.full_version)
print('scipy', scipy.version.full_version)

numpy 1.23.5
scipy 1.9.3

n = 10**0
d = 5*10**5

stdmin = rng.uniform(-2, -1, size=d)
stdmax = rng.uniform(1, 2, size=d)
mean = rng.normal(size=d)
std = np.exp(rng.normal(size=d))

%time truncnorm.rvs(stdmin, stdmax, mean, std, size=[n, d], random_state=rng)
%time truncnorm_rvs(stdmin, stdmax, mean, std, size=[n, d])
%time rng.normal(mean, std, size=[n, d])

CPU times: total: 109 ms
Wall time: 110 ms
CPU times: total: 46.9 ms
Wall time: 46.8 ms
CPU times: total: 0 ns
Wall time: 0 ns

大幅に改善されていた.
それでも自前実装の方が速いが³.

1. 検「算」ではないが. ↩

2. コルモゴロフ-スミノルフ検定等を使ってもいいが手間の割に安定しないので目視で済ます. ↩

3. そんなことより NumPy 1.21 -> 1.23 で numpy.random.Generator が爆速になってる方が目を引く. ↩