LoginSignup
13
9

More than 1 year has passed since last update.

@RAD0N

[python] kd木を使った最近傍探索

Last updated at Posted at 2022-02-25

説明

k-最近傍法（k-NN）アルゴリズムの勉強をしている時に、最近傍点を探すのにすべての点に対して計算していく（線形探索と呼ばれる）ととても効率が悪いということを聞いた。
効率よく探索する方法の一つにkd木というデータ構造をつかうものがあるらしいので、それを自分で実装してみた。
そして実際どの程度はやいのか、線形探索とkd木、そしてsklearnのNearestNeighborsを比較した。

参考：Kd-treeと最近傍探索 https://hope.c.fun.ac.jp/mod/resource/view.php?id=15284

実行環境

  • Intel(R) Core(TM) i7-8700 6コア12スレッド
  • メモリ16GB
  • windows10 64bit
  • 仮想8コア、物理4コア
  • Python 3.8.11
  • ANACONDA
  • JupyterLab 3.1.7

コード

モジュール

modules
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import time

線形探索

Linear
class Linear:
    def __init__(self,pointlist):
        self.pointlist = np.array(pointlist)
    def search(self,point,q=1):
        length = []
        for i in self.pointlist:
            length.append([self.L2(i,point),list(i)])
        if q == 1:
            return [i[1] for i in sorted(length)][0]
        else:
            return [i[1] for i in sorted(length)][:q]
    def L2(self,point1,point2):  #L2ノルムの意味。ユークリッド距離を計算する
        point1 = np.array(point1)
        point2 = np.array(point2)
        return np.linalg.norm(point1-point2)

動作テスト

Linear-test
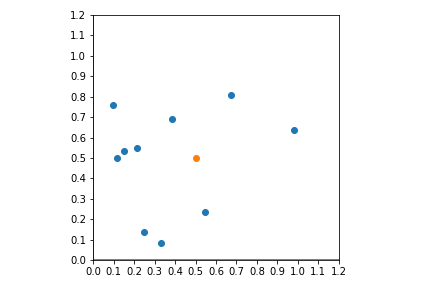
np.random.seed(19)

#0~1の乱数による10×2のnumpy配列(二次元の点10個とする）
data = np.random.random_sample((10,2))
point = [0.5,0.5]#この点からもっとも近い点を調べる

#グラフに示す
plt.scatter([i[0] for i in data],[i[1] for i in data])
plt.scatter(point[0],point[1])
plt.axis('square')
x,y = 1.1,1.1
plt.xlim(0,x) #x軸範囲指定
plt.ylim(0,y) #y軸範囲指定
plt.xticks(np.arange(0, x+0.1, step=0.1))
plt.yticks(np.arange(0, y+0.1, step=0.1))
plt.axhline(0, linewidth=2, color="gray")
plt.axvline(0, linewidth=2, color="gray")
plt.show()

a = Linear(data)
print(a.search(point))

データ（青い点）とクエリで示された点（オレンジ）
img.png

answer
[0.387006768446549, 0.6883273834221644]

おそらくちゃんと機能している

kd木

仕組み

とても説明しづらいがざっくりと説明したい
自分の説明はわかりづらいので以下のpdfを見ることをお勧めする。
Kd-treeと最近傍探索 https://hope.c.fun.ac.jp/mod/resource/view.php?id=15284

今回説明するkd木はあくまで自分が採用した方法であり、他にも微妙に違ったkd木の作り方とかあるらしい。
二次元データを例として使う
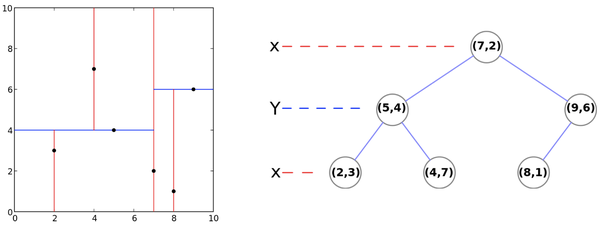
kd-tree
[出典] https://medium.com/@schmidt.jerome/k-d-trees-and-nearest-neighbors-81b583860144
kd木のデータ構造は、データの軸をずらしながら、それぞれの軸の中央値を取ることで作ることができる
中央値といっても厳密な意味ではなくデータ数が偶数の時は中央らしき二つの点のうち大きい方になる

具体的には上の図のように、はじめx軸のみを見て6つの点のうち4番目にある(7,2)が初めに来る。
その左には、図で(7,2)より左側にある3つの点をy軸で見たときに中央に位置する(5,4)が来る。
反対に右には(7,2)より右側の2つの点のうちy軸から見て中央として計算される(9,6)が来る。
そして(5,4)の左右には(5,4)で分割された(2,3)と(4,7)がくる。
(9,6)は右がなく左に(8.1)がくることとなる。

このように空間が長方形で区切られる。
二次元データに限らずこういう風にしてkd木を作ることができる。

そしてこのデータ構造を使った最近傍点の探し方だがこれが複雑である。
まず上の図の例で(4,3)に最も近い点を探したいとする。
kd木にこの点をあてはめる。図の右側の木を見たとき、(4,3)のxの値4は(7,2)の7より小さいので(7,2)の左にあり、次に(4,3)のyの値の3は(5,4)の4より小さいので(5,4)の左側（左側の図でいうと下側）に来るので(2,3)と一緒になる。
ここで最後に行きついた(2,3)の点と与えられた点(4,3)との距離を計算しておく(今回値は1)。
そして今度は木を上に向かってさかのぼる。まず親の(5,4)を見てy軸の値を比較する。
親(5,4)と(4,3)のyの値の差は1であり、これは先ほど計算しておいた1以下の値である。
これはつまり(5,4)とその右に位置するノードの中に(2,3)よりも(4,3)に近い点が存在する可能性があるということなので(5,4)とその右側の(4,7)を最近傍点の候補として保持する。
さらに(5,4)の親の(7,2)についてみる。(7,2)と(4,3)のxの値の差は3であり、この値は計算しておいた値(1だった)よりも大きい。つまり(7,2)自身とそれより右側の点はすべて計算する必要がないことが分かる。
最後に、行きついた点(2,3)と候補になっていた(5,4)と(4,7)と与えられた点(4,3)との距離を計算し、結局(5,4)が最最近傍点であるとわかる。

このようにどれかの軸についての絶対値を比較するという簡単な計算で絶対に最近傍点の存在しない領域を排除することができる。
kd木の探索を図であらわすと以下のように、いきついた点との距離を半径として与えられた点を中心とする円とかぶさる長方形の中の点のみを調べているということがわかる。
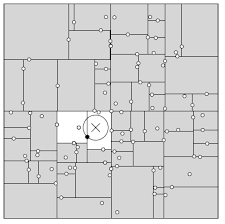
kd-tree
[出典] Kd-treeと最近傍探索 https://hope.c.fun.ac.jp/mod/resource/view.php?id=15284

コード

kd-tree
class KD:
    def kdtree(self,pointList, depth=0):#kd木を構築
        pointList = np.array(pointList)
        if not len(pointList):
            return
        pointList = pointList.tolist()
        k = len(pointList[0]) # 全ての点が同じ次元を持つと仮定
        axis = depth % k
    
        # 点のリストをソートし、中央値の点を選択する
        pointList.sort(key=lambda x:x[axis])
        median = len(pointList)//2 # 中央値を選択
        
        pointList = np.array(pointList)
        # ノードを作成し、部分木を構築する
        kd = KD()
        kd.axis = depth % k
        kd.pointList = pointList
        kd.location = pointList[median]
        kd.leftChild = self.kdtree(pointList[0:median], depth+1)
        kd.rightChild = self.kdtree(pointList[median+1:], depth+1)
        self.kd = kd 
        return kd
    
    
    def L2(self,point1,point2):#L2ノルム
        point1 = np.array(point1)
        point2 = np.array(point2)
        return np.linalg.norm(point1-point2)
    
    def search(self,point,q=1):#入力された点(point)の最近傍点を探す
        for i in range(q):
            trees = [self.kd]
            notice_list = []
            while len(trees) > 0:
                if trees[0]==None:
                    del trees[0]
                    continue
                data = self.neighbourhood(trees[0],point)
                notice_list+=data[0]
                trees+=data[1]
                del trees[0]
            min_point = None
            length = float("inf")
            for j in [(self.L2(i.location,point),i) for i in notice_list]:
                if length > j[0]:
                    min_point = j[1]
                    length = j[0]
            return min_point
    
    def neighbourhood(self, start_tree,point):
        #searchのための関数。start_treeから順番に、与えられた点に近いほうへ進んでいく。
        axis = start_tree.axis
        tree = start_tree
        p = []
        while True:
            if tree == None:
                break
            s = point[axis] - tree.location[axis]
            if s <= 0:
                p.append((abs(s),tree.rightChild,tree))
                tree = tree.leftChild
            elif s > 0:
                p.append((abs(s),tree.leftChild,tree))
                tree = tree.rightChild
            axis+=1
            axis = axis%len(point)
        l2 = self.L2(p[-1][2].location,point)
        return ([p[-1][2]]+[i[2] for i in p if i[0]<=l2],[i[1] for i in p if i[0]<=l2])

動作テスト

kdtree-test
np.random.seed(19)

data = np.random.random_sample((10,2))
point = [0.5,0.5]

plt.scatter([i[0] for i in data],[i[1] for i in data])
plt.scatter(point[0],point[1])
plt.axis('square')
x,y = 1.1,1.1
plt.xlim(0,x) #x軸範囲指定
plt.ylim(0,y) #y軸範囲指定
plt.xticks(np.arange(0, x+0.1, step=0.1))
plt.yticks(np.arange(0, y+0.1, step=0.1))
plt.axhline(0, linewidth=2, color="gray")
plt.axvline(0, linewidth=2, color="gray")
plt.show()

b = KD()
tree = b.kdtree(data)#kd木構築
print(b.search(point).location)#探索

データ（青い点）とクエリで示された点（オレンジ）
img.png

answer
[0.38700677 0.68832738]

機能しているようだ。
線形探索の時に比較して桁数が足りていないように見えるが、これはnumpy配列で表示しているからであり、pythonのリストに変換して確かめるとちゃんと値が一致していることが分かる

sklearn

sklearnも試しておく。非常に使いやすい。

sklearn
from sklearn.neighbors import NearestNeighbors 

np.random.seed(19)

data = np.random.random_sample((10,2))
point = [0.5,0.5]

knn_model = NearestNeighbors(n_neighbors=1, algorithm='ball_tree').fit(data) 
distances, indices = knn_model.kneighbors([point])

print(data[indices[0]][0])
answer
[0.38700677 0.68832738]

比較

これまでの線形探索とkd木、sklearnを比較する

比較用の関数

comparison
def comparison(data,point,size=1,seed=None,d=2):
    if seed:
        np.random.seed(seed)
    data = np.random.rand(data,max(2,d))*1000
    points = np.random.rand(point,max(2,d))*1000

    plt.scatter([i[0] for i in data],[i[1] for i in data],s=size)
    plt.scatter([i[0] for i in points],[i[1] for i in points],color='red',s=size)
    
    plt.axis('square')
    x,y = 1000,1000
    plt.xlim(0,x) #x軸範囲指定
    plt.ylim(0,y) #y軸範囲指定
    plt.xticks(np.arange(0, x+1, step=100))
    plt.yticks(np.arange(0, y+1, step=100))
    plt.axhline(0, linewidth=2, color="gray")
    plt.axvline(0, linewidth=2, color="gray")
    plt.show()
    start_time = time.perf_counter()
    a = closest(data)
    ans1 = []
    for i in points:
        ans1.append(a.search(i))
    end_time = time.perf_counter()
    print("線形探索の答え : ",ans1[:3],"......")
    print("線形探索の時間 : ",end_time-start_time)
    
    
    start_time = time.perf_counter()
    b = KD()
    tree = b.kdtree(data)
    ans2 = []
    for i in points:
        ans2.append(b.search(i).location)
    end_time = time.perf_counter()
    print("kd木の答え : ",ans2[:3],"......")
    print("kd木の時間 : ",end_time-start_time)


    from sklearn.neighbors import NearestNeighbors 
    start_time = time.perf_counter()
    knn_model = NearestNeighbors(n_neighbors=1, algorithm='ball_tree').fit(data) 
    distances, indices = knn_model.kneighbors(points)
    ans3 = [data[i] for i in np.ravel(indices)]
    end_time = time.perf_counter()
    print("sklearnの答え : ",ans3[:3],"......")
    print("sklearnの時間 : ",end_time-start_time)

この関数を実行することで1~1000までのランダムな数の集合について、与えられたランダムな点のリストすべての最近傍点を計算した、線形探索、kd木、sklearnの結果と実行時間を見ることができる。
またデータの初めの2要素のみ平面にプロットする
引数はdataがもとの点の数、pointが最近傍点を求めたい点の数、sizeが表示するグラフの点の大きさ、seedが乱数のシード値（指定しなければランダム）、dがデータの次元（デフォルトで2次元データ）

実際に比較する

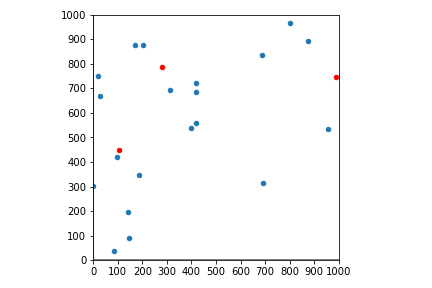
20個のデータの中から3個の点それぞれの最近傍点を出す

まずは20個のデータから3個の点の最近傍点を調べてみる

test
comparison(data=20,point=3,size=20,seed=1)

graph

ans
線形探索の答え :  [[876.3891522960383, 894.6066635038474], [313.42417815924284, 692.3226156693141], [98.3468338330501, 421.10762500505217]] ......
線形探索の時間 :  0.0007680000016989652
kd木の答え :  [array([876.3891523, 894.6066635]), array([313.42417816, 692.32261567]), array([ 98.34683383, 421.10762501])] ......
kd木の時間 :  0.0011911999972653575
sklearnの答え :  [array([876.3891523, 894.6066635]), array([313.42417816, 692.32261567]), array([ 98.34683383, 421.10762501])] ......
sklearnの時間 :  0.0006977999983064365

sklearnが微妙に線形探索よりもはやく、その二つよりkd木が遅い。
kd木の構築のプログラムがネックになっていると思われる。

10000個のデータの中から10個の点それぞれの最近傍点を出す

次に少しデータを増やして10000個のデータから10個の点の最近傍点を調べてみる

test
comparison(data=10000,point=10,size=1,seed=1)

グラフに意味がなくなった
graph

ans
線形探索の答え :  [[808.7170955700695, 538.131802303424], [879.1175147772752, 949.5105912291732], [835.1899366371584, 993.8457804675411]] ......
線形探索の時間 :  0.9039671999999825
kd木の答え :  [array([808.71709557, 538.1318023 ]), array([879.11751478, 949.51059123]), array([835.18993664, 993.84578047])] ......
kd木の時間 :  0.16292650000002595
sklearnの答え :  [array([808.71709557, 538.1318023 ]), array([879.11751478, 949.51059123]), array([835.18993664, 993.84578047])] ......
sklearnの時間 :  0.0045610999999894375

sklearnがすさまじくはやいが、kd木が線形探索を抜かした。
kd木の説明の最後の図のように、元のデータが多いとkd木で排除できる点が多いので計算量が少なくて済むのだろう。
sklearnのプログラムは謎である。

10000個のデータの中から100個の点それぞれの最近傍点を出す

今度はさらに調べる点の数を増やして10000個のデータから100個の点の最近傍点を調べてみる

test
comparison(data=10000,point=100,size=1,seed=1)

graph

ans
線形探索の答え :  [[808.7170955700695, 538.131802303424], [879.1175147772752, 949.5105912291732], [835.1899366371584, 993.8457804675411]] ......
線形探索の時間 :  98.44023679999998
kd木の答え :  [array([808.71709557, 538.1318023 ]), array([879.11751478, 949.51059123]), array([835.18993664, 993.84578047])] ......
kd木の時間 :  0.5181100000000356
sklearnの答え :  [array([808.71709557, 538.1318023 ]), array([879.11751478, 949.51059123]), array([835.18993664, 993.84578047])] ......
sklearnの時間 :  0.009022799999968356

線形探索がいかに遅いかということがよくわかる結果となった。線形探索はkd木の約200もの時間がかかっている。これは、線形探索は最近傍点の知りたいデータ一つ一つについて、元のデータすべてとの距離を計算しているのに対し、kd木が先ほど述べたように計算量を大きく削減しているからである。
この差はより多くのデータに対して最近傍点を探索しようとすると、さらに大きくなっていく。
sklearnはまた桁違いでkd木の50分の1の時間で終わっている。
どのようなアルゴリズムを使っているのか見当もつかない

次元を増やす

詳しい理屈は知らないが、kd木は次元数を増やすと計算量があまり削減できなくなるという話を聞いた。
試してみようと思う
先ほどの例を10次元にしてみる

test
comparison(data=10000,point=100,size=1,seed=1,d=10)
ans
線形探索の答え :  [[351.1195174462909, 581.5991613909572, 136.65488859355546, 556.662647361485, 786.3959709414942, 636.9884337395181, 706.8418775762096, 42.2006166438752, 343.427919387712, 282.72487579193563], [866.8730265976224, 219.30754511904894, 389.01282952543016, 217.85420169671931, 60.959104237129466, 92.4262267827537, 498.02905563951686, 873.6334168665475, 786.433939315744, 354.1145481627519], [962.569934373361, 968.6646245962836, 952.4107797833416, 259.0817165778683, 723.9252012772273, 9.691044119441328, 163.87095551164677, 88.38034391817884, 709.9605421187368, 636.3093144380106]] ......
線形探索の時間 :  104.9682029999999
kd木の答え :  [array([351.11951745, 581.59916139, 136.65488859, 556.66264736,
       786.39597094, 636.98843374, 706.84187758,  42.20061664,
       343.42791939, 282.72487579]), array([866.8730266 , 219.30754512, 389.01282953, 217.8542017 ,
        60.95910424,  92.42622678, 498.02905564, 873.63341687,
       786.43393932, 354.11454816]), array([962.56993437, 968.6646246 , 952.41077978, 259.08171658,
       723.92520128,   9.69104412, 163.87095551,  88.38034392,
       709.96054212, 636.30931444])] ......
kd木の時間 :  169.5636930999999
sklearnの答え :  [array([351.11951745, 581.59916139, 136.65488859, 556.66264736,
       786.39597094, 636.98843374, 706.84187758,  42.20061664,
       343.42791939, 282.72487579]), array([866.8730266 , 219.30754512, 389.01282953, 217.8542017 ,
        60.95910424,  92.42622678, 498.02905564, 873.63341687,
       786.43393932, 354.11454816]), array([962.56993437, 968.6646246 , 952.41077978, 259.08171658,
       723.92520128,   9.69104412, 163.87095551,  88.38034392,
       709.96054212, 636.30931444])] ......
sklearnの時間 :  0.13422899999977744

なんとkd木が線形探索よりも遅くなった。
これはkd木が高次元だとほぼ探索するデータを削減することができないので、結果kd木を構築したり探索するときにリストを繰り返し書き換えたりする時間がかさんで線形探索よりも遅くなるのだと考えられる。
sklearnはまた凄い速さである

自分でkd木を実装してみて仕組みが理解できたのはとてもよかった。

実際のプログラム上ではsklearnのNearestNeighborsを使いましょう

13
9
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
13
9