概要
『LMIによるシステム制御 ロバスト制御系設計のための体系的アプローチ』 (蛯原義雄, 森北出版)の1章の問題をPython(cvxpy)で実装してみた.
この記事で得られること:
- Pythonを用いて、線形行列不等式(LMI; Linear Matrix Inequality)を解く.
- Pythonを用いて、制御器を設計し、倒立振り子の数値シミュレーションを行う.
- 具体的な例を通して、cvxpyの使い方をまとめる.
何で書こうと思ったか
PythonでLMIを解くときには、限られた選択肢しかない.(参考:PythonのSDP実行時間比較)
さらに、困ったことに、cvxpyでLMIを解く日本語の記事がほっっとんどない.
そのため、cvxpy 公式ドキュメントを読んで、試行錯誤...
その結果を、今後のためにも備忘録的にまとめておくことにした.
問題設定と求解すべきLMI
問題設定
台車型倒立振り子を以下の連続時間の状態空間表現でモデル化する.
\dot{x}(t) = Ax(t)+Bu(t) \\
y(t) = Cx(t)
ここで、入力を$u(t)$, 状態を $ x(t)=[z, \theta, \dot{z}, \dot{\theta}]^T $ , 出力を $ y(t)=[z, \theta]^T $ とし、係数行列を以下で与える. (入力はモータに流れる電流、$z$は台車位置、$\theta$は振り子の角度)
A = \begin{bmatrix}
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
0 & -m^2gl^2 & -FqW & cmlW \\
0 & mglpW & FmlW & -cpW
\end{bmatrix}, \ \ B=\begin{bmatrix} 0 \\ 0 \\ aqW \\ -amlW \end{bmatrix} \ \
C = \begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
\end{bmatrix} \\ \left( p = M + m + \frac{J_c}{r^2}, \ q = J_p + ml^2, \ W = \frac{1}{pq - m^2l^2} \right)
(詳しいパラメータの意味や値は本質的ではないので、ここでは割愛)
この制御対象に対し、
- 閉ループシステムを安定化する
- 初期状態が平衡状態からずれていても、すみやかに平衡状態に整定する
- 角度が $ \pi / 36 $ から制御を開始した時の制御入力の振幅が1.2を超えない (初期状態が $x(0)=B_{w_2}=[0, \pi / 36, 0, 0]^T$ から制御を開始したとき)
という要件を満たす状態フィードバック制御器 $ u=Ky $ を設計する.
LMI
設計仕様を定式化すると、次のLMIを満たす $X, Y$ を求め、$K = YX^{-1}$ で定めればよい.(導出は参考文献の本をご確認ください)
\begin{bmatrix}
\mathrm{He} (AX+BY) & * \\
C_{z_2}X+D_{z_2u} Y & -\gamma I_5 \\
\end{bmatrix} \prec 0, \ \
\begin{bmatrix}
X & * \\
B_{w_2} & 1
\end{bmatrix} \succ 0, \ \
\begin{bmatrix}
X & * \\
Y & 1.2^2
\end{bmatrix} \succ 0
ただし、$C_{z_2}, D_{z_2u}$ は以下.
C_{z_2} = [I_4, 0_{4, 1}]^T, \ \ D_{z_2u}=[0_{1, 4} 1]^T
また、$\mathrm{He}(A)=A+A^T$である.
実際に求解する際には、上のLMIを制約として、$\gamma$を最小化する半正定値計画問題を解くことになる. ()
使用するライブラリ
ここでは、以下のライブラリを使用する.
- numpy
- matplotlib
- control (制御工学ライブラリ)
- cvxpy (LMIを求解するためのライブラリ)
import numpy as np
from matplotlib import pyplot as plt
from control import matlab
import cvxpy as cp
プログラム
- 状態方程式の作成
- LMI条件の作成
- 求解
- 制御器の復元
- シミュレーション
状態方程式の作成
パラメータの宣言
l = 0.15
m = 0.0402
Jp = 0.00030142
M = 0.6862
Jt = 1.34 * 10**(-4)
Jm = 1.30 * 10**(-7)
Jc = Jt + Jm
r = 0.02485
F = 0.36
c = 0.0015
g = 9.80665
a = 1.9
p = M + m + Jc/(r*r)
q = Jp + m*l*l
W = 1/(p * q - m * m * l * l)
係数行列の作成
A = np.array([
[0, 0, 1, 0],
[0, 0, 0, 1],
[0, -m*m*g*l*l*W, -F*q*W, c*m*l*W],
[0, m*g*l*p*W, F*m*l*W, -c*p*W]
])
B = np.array([[0, 0, a*q*W, -a*m*l*W]]).T
C = np.array([[1, 0, 0, 0], [0, 1, 0, 0]])
D = np.zeros((2, 1))
# 今回は使わないが、状態空間の生成は以下
sys = matlab.ss(A, B, C, D)
そのほかの変数
LMI条件に必要な行列の宣言
Bw2 = np.array([[0, np.pi / 36, 0, 0 ]]).T # 初期状態
Cz2 = np.array(np.eye(5, 4)) # 対角成分が1. それ以外は0
Dz2u = np.array([[0, 0, 0, 0, 1]]).T
LMI条件の作成
変数宣言
cp.Variable()で、変数の宣言が可能. 第一引数に(必要であれば)行列の型をタプルで渡す.
symmetric=Trueとすると、対称行列であることを条件として課すことができる. (そのほか、nonneg=TrueやPSD=Trueなどがある1 )
X = cp.Variable((4, 4), symmetric=True)
Y = cp.Variable((1, 4))
gamma = cp.Variable()
LMI制約の定義
LMI制約に必要な関数 $\mathrm{He}(A)=A+A^T$ の定義.
def He(X):
return X + X.T
LMI制約を定義する.
cvxpyの変数を含んだ行列のブロック定義は cp.bmat()で行う.
混同注意!
cvxpyの変数を含まず、numpy配列のみで行列のブロック定義を行う場合は、np.block()で十分.
strictな正定(負定)条件M2 > 0はエラー(Strict inequalities are not allowed.)が出るので、半正定条件としておく(M2 >> 0).
M1 = cp.bmat([
[He(A @ X + B @ Y), (Cz2 @ X + Dz2u @ Y).T],
[Cz2 @ X + Dz2u @ Y, -gamma * np.eye(5,5) ]
])
M2 = cp.bmat([
[X, Bw2],
[Bw2.T, np.matrix(1)]
])
M3 = cp.bmat([
[X, Y.T],
[Y, np.matrix(1.2 * 1.2)]
])
# LMI制約の配列
constraints = [ M1 << 0 , M2 >> 0, M3 >> 0]
求解
cp.Problem()で問題の定義. 第一引数に目的、第二引数に制約を渡す.
cp.Problem().solve()で求解. 求解の詳細が知りたければ、引数としてverbose=Trueを記述しておく.
prob = cp.Problem(cp.Minimize(gamma), constraints)
prob.solve()
# prob.solve(verbose=True)
以上を実行すると、最小化された$\gamma$として、0.16157841825111297 が得られる.
制御器の復元
制御器は $K=YX^{-1}$で与えられる.
求解後のcvxpyの変数の値は、変数名.valueで取得できる.
K = Y.value @ np.linalg.inv(X.value)
シミュレーション
閉ループ系の構成
状態フィードバックをかけたときの閉ループ系は以下で与えられる.
\dot{x}(t)=(A+BK)x \\
y = Cx
これを構成する.
A_ = A + B @ K
B_ = np.zeros((4, 1))
C_ = C
D_ = D
sys_cl = matlab.ss(A_, B_, C_, D_) # 状態空間モデル
時間応答の観察
matlab.initialで、システムのゼロ入力応答を取得する.
# 初期値応答
Td = np.arange(0, 10, 0.01) #シミュレーション時間
x0 = Bw2 #初期値
z, t, x = matlab.initial(sys_cl, Td, x0 ,return_x=True)
以下でグラフの描画
# 初期値応答の描画
fig, ax = plt.subplots()
ax.plot(t, x[:, 0], label = '$z$')
ax.plot(t, x[:, 1], ls = '-.', label = '$theta$')
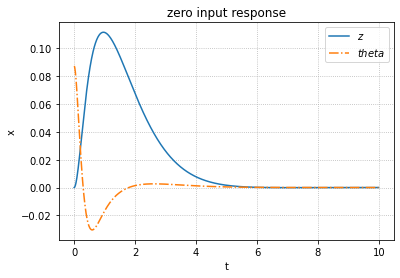
ax.set_title('zero input response')
ax.set_xlabel('t')
ax.set_ylabel('x')
ax.grid(ls=':')
ax.legend(loc='best')
plt.show()
描画結果:ちゃんと収束している.
まとめ
この記事では以下をPythonにより実装した.
- 倒立振り子の状態空間表現
- LMIの求解
- 制御器の作成と、時間応答シミュレーション
覚えたての備忘録なので、ミスは多めにみてもらえると嬉しいです. (機会があれば、出力フィードバック制御や、ロバスト制御のパターンも記事にしたい.)
参考文献
- 『LMIによるシステム制御 ロバスト制御系設計のための体系的アプローチ』(蛯原義雄, 森北出版, https://www.morikita.co.jp/books/mid/092101 )
- PythonのSDP実行時間比較 https://qiita.com/teatea/items/153f35af4b5eba873181
- cvxpy 公式ドキュメント https://www.cvxpy.org/index.html
- control.matlab 公式ドキュメント https://python-control.readthedocs.io/en/latest/matlab.html
-
詳しくは以下を参照されたい. https://www.cvxpy.org/api_reference/cvxpy.expressions.html#leaf ↩