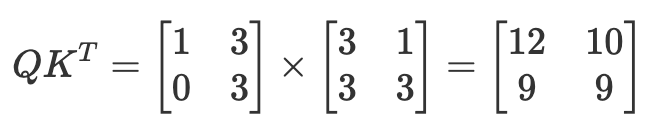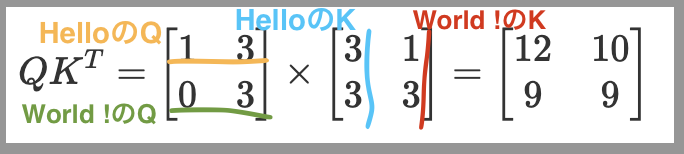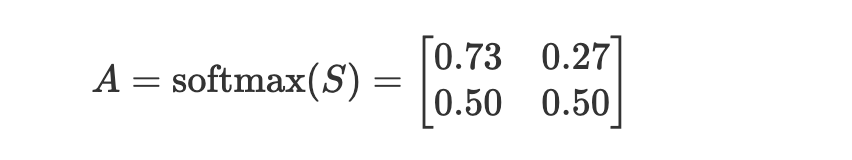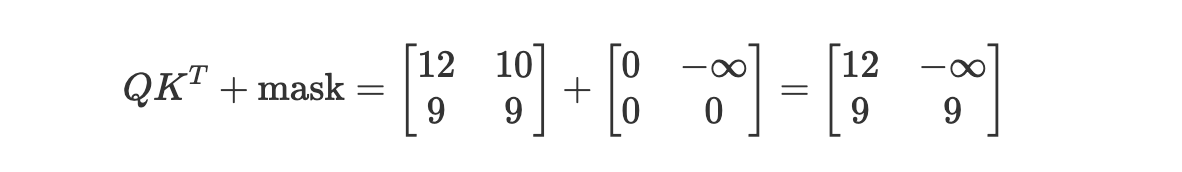注意
本記事はKaggleや決定木、NNを少しだけ触ったことのあるWebエンジニアがAttention機構理解のために調べながら書いています。
もっと詳しく知りたい方はぜひ「Attention Is All You Need」を読んでみてください
In This Article...
参画しているPJでViTやCNN等々を扱っていることもあり、根本理解をするためにTransformerで一般的に使われるAttentionの基本形として、Scaled Dot-Product Attention(以下SDPA)を題材に、Attention機構の仕組みを数学初心者でも追えるように噛み砕いて解説します。(というか自分も理解しながら書いていきます。ちなみに自分の嫌いな教科は数学と物理でした。)
今回は最初にそもそもSDPAがどんな問題を解く仕組みなのかを押さえ、その後推論過程において「Hello World!」という短い文字列を例にベクトル化 → 内積 → 行列計算の流れを確認し、最後に一般化した手順と PyTorch 実装をしようと思います。
この記事の目的
以下を理解すること
- Attentionとは何か?
- Scaled Dot-Product Attentionとは?
- SDPAの中では何が行われているのか?
想定読者
- 行列計算・確率統計が少しわかる
- 機械学習についてG検定レベルの前提知識がある
- (欲を言えば)Kaggleを少しやったことがある
- Attention機構の中身を理解したい
Attentionとは?
目線合わせとしてAttention機構とは?を説明します。
短くいうと、Attention = 「どの情報にどれだけ注目すべきか」を学習で決めて、重要な情報を取り出す仕組み。
人間が文章を読むとき「全部均等に読む」わけではなく、今の単語に関係の強い部分に注意を向けるように、transformerで「文章のどこに注意を向けるべきか?」を処理する仕組みが Attention。
このAttentionは以下の特徴を持つらしい。
ここら辺もこの記事で注目ポイントにできたらいいなと。
- 全ての単語が全ての単語を見られる(Self-Attention の場合)
- 「文脈理解」や「依存関係の抽出」に強い
- RNN のように順番に処理せず、一度に並列計算できる
Scaled Dot-Product Attentionとは?
2017年に公開されたTransformerを発表した論文「Attention Is All You Need」に記載のあるAttentionの最も基本形となるもの。
日本語にすると、正則化(Scaled)内積(Dot-Product)注意(Attention)
内積とは行列計算のドット積のこと。
前述したが、Transformerで一般的に使われるAttentionの基本形になる。
SDPAで行われること
- 埋め込みベクトルから Query・Key・Value を線形変換で用意する
- Query と Key の内積を取り、必要に応じてマスクを掛けつつ
√d_kで割ってスケールする。 - スケール後のスコアにソフトマックスを適用し、アテンション重み(確率のような値)を得る。
- アテンション重みで Value を重み付き平均し、文脈を取り入れた出力ベクトルを作る(ドロップアウトなどを挿入する場合もある)。
という流れで動作する。
とはいえ、これだけではわからない部分が多いのでSPDAへの入力文字列が"Hello World !"だった時にどのようにこれが処理されるのかを見ていく。
Hello World!が処理される流れを追う
工程1. 文字列をトークンに分解する
自然言語処理では文字列をそのまま扱わず、まず単語やサブワード単位(トークン)のモデルが扱える最小単位に分割する。
これをトークナイゼーションという。
ここではシンプルに空白で区切り、文末記号も 1 つのトークンとする。
入力: "Hello World!"
トークン列: ["Hello", "World!"]
古くはMeCab, Juman, Sudachiなどの形態素解析ベースだったが、
今の大規模言語モデル(LLM)はBPE や SentencePiece によるサブワード分割が主流らしい。
形態素解析によるトークナイズ
例:「私は学生です」 → 「私 / は / 学生 / です」
統計的なサブワード分割
例:「私は学生です」 → 「▁私 / は / 学 / 生 / です」
こうすることで未知語にも強く、言語を問わず統一的に使えるとのこと。
つまり、どのような単位でモデルに文章を扱わせるか?が変わってきている。
工程2. 各トークンを埋め込みベクトルに変換する
機械学習モデルではトークンを数値のベクトルに置き換えて数値的に扱う。
これを埋め込み / Embeddingと呼び、ベクトルの列数は Dense(埋め込み次元)と表現される。
また、次元が増えると各トークンの特徴をより細かく表現できるようになる。
ただし、可愛さなのか、頻出度合いなのか、各次元が何を表しているのかはわからない。
一般的なTransformerでは200~1000程度の次元数を利用するとのこと。
行がトークン、列が次元という見た目になるため、表(行列)で眺めるとイメージしやすい。
LLMだととんでもない次元数で扱うが、今回は簡単のため次元数を3にする。
例として埋め込みベクトルが以下のようになったものとする。
| トークン | 埋め込みベクトル (Dense = 3) |
|---|---|
| Hello | [1, 2, 1] |
| World! | [0, 1, 2] |
この表を行列として書くと次のようになる。
HelloとWorld!のベクトルはどこからくる??
このHelloとWorld !にあたるベクトルは学習を通じて「似た文脈で使われる単語ほど近いベクトルになる」よう自動調整される。逆にいうとこのベクトルを作り出すのが学習という段階になる。
BERT や GPT などの大規模モデルでも同じで、膨大なコーパス(大量のテキストを集めたデータの集合)を使って埋め込みを更新しながら意味を捉える空間を作り上げていく。
つまり今回は事前の学習段階でHelloというトークンが[1,2,1]というベクトルに学習されたのち、推論過程でHello World!が入力され、Helloが[1,2,1]というベクトルにEmbeddingされたということになる。
工程3. 埋め込みベクトルに重み行列を掛けてQ, K, V をつくる
Q/K/Vは後で解説するとして、一旦この工程でやることだけ解説します。
SDPAでは埋め込みベクトルに3種類の重み行列(学習パラメータ)を掛けて、Query (Q)、Key (K)、Value (V) を作る。
重み行列は事前に行列数だけ決めておき、学習の中で調整される。
ここでは出力次元(Q/K/Vの次元)を2に揃えた例を示す。
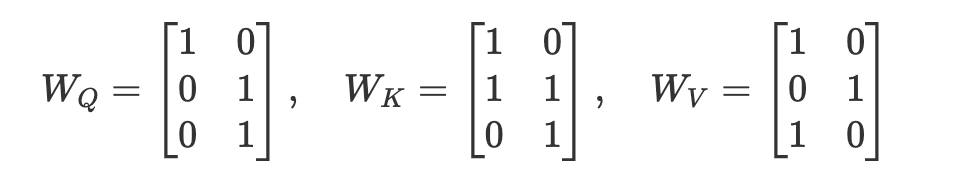
埋め込み行列 $E$ に左から掛けると、Q/K/V はそれぞれ次の 2 次元ベクトル(行列)になる。
- 行方向はトークン(Hello, World!)、
- 列方向は Q/K/V の次元(ここでは 2)
を表す
重み行列 WQ/WK/WVとは?
埋め込みベクトルにこれら三つを掛けることで、行列の一行一行になっているトークン達がそれぞれ何をしたいの?という情報を作り出せる行列のこと。
それぞれ以下の役割がある。
$W_Q$(Queryの重み)
あるトークンが「どんな情報を探したいか(文脈から何を拾いたいか)」を表現できるように変換する
$W_K$(Keyの重み)
トークン自身が「どんな特徴を提供できるか」を示すベクトルに変換する
$W_V$(Valueの重み)
実際に引き渡す内容(情報本体)を、後段が利用しやすい形に変換
各トークン(HelloとWorld!)の埋め込みベクトルに $W_Q$ を掛けると、「このトークンは今どんな情報を探したいのか」を表す Q ベクトルに変換されます。同様に $W_K$ を掛けると「自分はどんな情報を持っているか」を表す K ベクトルになる。
4. QとKを掛けて類似度(スコア)を測る
いきなりだが、内積(ドット積)は同じ方向をむくベクトル同士だと大きくなり、直交するベクトル同士だと小さくなる性質がある。
このことから、Query と Key の内積(ドット積)を計算すると、どのトークン同士が関連しそうかを数値化して大小比較できることになる。
これは先ほどのQ(どんな情報が欲しいか?)と、K(私はどんな情報を提供できる)という情報をトークン同士でマッチングさせるイメージに近い。
さらに踏み込むと、「探したい性質を持っているトークンほどスコアが高くなる」ように学習が行われているということになる。
計算としては以下のように行われる。
Kが転置(T)されているのは、Qの行方向の各トークンにKのトークン(行方向)を掛け合わせるため。
転置することで以下の画像のようになり
- HelloのQとHelloのKをかけたスコアの12(左上)
- HelloのQとWorld!のKを掛けたスコアの10(右上)
- World!のQとHelloのKをかけたスコアの9(左下)
- World!のQとWorld!のKをかけたスコアの9(右下)
を求めることができる。
この結果の解釈は、
右上の10の場合、HelloがWorldに10の注意を向けているという理解になる。
ただし、HelloがHello自身に12、HelloがWorld!に10の注意を向けていると言われても解釈しにくい。
また、このままだと次項で話す内積をとったままの値における課題が残るため、次の工程で内積の値の大小を揃え、どのトークンがどのトークンにどの程度注意を向けているかを確率的に解釈可能にする
工程5. スコアを確率として解釈可能にする
ここからScaled Dot-Product AttentionのScaledとAttentionが出てきます
5-1.内積をとったままの値における課題への対応
先ほどの例は二次元の話だったが、前述の通り一般的なTransformerの場合、200以上の次元が用いられる。
ベクトルの次元が大きいと、内積で掛け合わせ&足し合わせる項がその分増えるので、値がどんどん大きくなったり、あるいは極端に小さくなる部分が出やすくなる。
こうなると、極端に大きなトークンにのみ注意が向くことになり、他のトークンが無視されやすくなってしまう。
これを防ぐために、Key の次元数$d_k$の平方根で割ってスケール(正則化)する。
つまり極端にデカい、極端に小さい値の幅を小さくする。
→平均ではなく$√d_k$でスケールする理由は後述の”5−1 補足:平均ではなく√d_kでスケールする理由”を読んでほしい
これが、SPDAの先頭にScaledがついている理由。
5-2 確率への変換
ソフトマックス関数にかけ、各トークンがどのトークンに注意を向けているのか確率的に解釈できるようにする。
この$A$をアテンション重み(注意重み)といいます。
SPDAのAはAttentionでしたね!!!!!1
ソフトマックス関数は次の性質を保つためこれが可能になる
・値を0-1の範囲に収める
・合計が1になるため、各値が確率として解釈可能になる。
例えば、AにおけるHelloの部分を見てみると、
左上の0.73と右上の0.27を足すと1になり、
これは以下のような解釈が可能になる。
- HelloがHello自身に73%の注意を向けている
- HelloがWorld!に27%の注意を向けている
ここまでで、各トークンがどのトークンにどれだけ注意を向けているのかがわかるようになりました。
ただ忘れていないだろうか、重み付き行列として出てきた$W_V$の存在を。。
こいつがこの後伏線回収します。
工程6 文脈の情報を付与する。
お疲れ様です、これで最後の工程です!
この工程では$A$(Attention重み)からSPDAの最終出力である$O$(Output)を作ります。
ここまでHello World!がAttention重みへと変換される工程を見てきましたが、今の状態にも一つ問題があります。それは、文脈の情報を含んでいないということです。今までLLMやChatGPTを利用してきた中で、そっちの意味じゃないんだよな、、、という経験ありませんか?
例えば、今の「Hello World!」も、ソフトウェアエンジニアでなければ2019年公開のSF映画だと思う人もいるかもしれない。
そこで、最後にこのAttention重みに文脈の情報を付与します。
そこで出てくるのが工程3で出てきた$Q_V$(Valueの重み行列)
をかけることで、どういう文脈で使われている単語(トークン)なんだよ!をわかるようにしてあげます。
つまり、Vは学習段階において、Programmingという単語の近くにHello World!!が出るパターンと、映画という単語の近くにHello World!!が出るパターンをそれぞれ適切に処理できるように、プログラミングっぽさと映画っぽさを特徴として浮かび上がらせることができるように重みを調節して行っているわけですね。
というかそれができるように学習されてるV、すげえ
そして、最終的に、各トークンは周囲の文脈を取り入れた新しい特徴量を得て、後段の層(例: フィードフォワードネットワーク)に渡されていくのでした、、、
最後に
QKVを作れるようにしてるのすげえ。全てがQKVが学習段階で作られるために上記で説明したことが成り立っているわけで、それを作れるようにしたのすごいわ〜〜という感想。
ここまででScaled Dot-Product Attentionについて書いてきましたが、学習段階や、Multi-Head Attention、誤差逆伝播法など、まだまだちゃんと理解していないので引き続きQiitaを書いていきます!
補足
5-0 Attentionマスクについて
今回は推論時かつパディングがなく、KVキャッシュで過去の回答を取得するようなケースではなかったため省略したが、実務上・実装上は以下の二つのAttentionマスクをかけるとのこと。
どちらも、不要な位置に注意を向けないように -inf を入れてソフトマックス後の重みを 0 にする役割を持つ。
これがないと、学習段階で生成すべき文章がわかってしまったり、推論時に高速化するため、過去計算したキャッシュを流用すると、本来まだ生成していない文章に注意が向いてしまったりするらしい。
-
因果マスク
自己回帰モデルが未来トークンを覗いてズルをしないように、現在より後ろの位置を遮断する。
学習時:損失に影響しないよう常に除外。
推論時:パディングを参照するとノイズになるため常に無視。 -
パディングマスク
バッチ内で長さを揃えるために埋めた<pad>のようなダミートークンを完全に無視させる。
学習時:教師データには未来の単語が並んでいるので、マスクで隠す。
推論時:過去の K/V をキャッシュしつつ未来側へ注意が飛ぶのを防ぐ。
例えば、パディングや因果マスクをかける場合、このスコア行列に -inf を足してソフトマックス時に 0 になるようにする。
例えばシーケンス長 2 の因果マスクは以下のようなイメージ。
これを適用することで、学習時にHelloだけ生成した段階でWorldが見えてしまうのを防ぐ。
5−1 補足:平均ではなく√d_kでスケールする理由
結論を言えば、以下のアイデアを適用したもの。
- 確率統計では、値のばらつき(分散)を抑えるために標準偏差(√分散)で割る
なら、分散に比例して大きくなる値(次元数)を、分散の平方根である標準偏差(√次元数)で割ってやれば、標準偏差と同じように値のばらつきを抑えられるということ。
(正確には次元数に比例して分散が大きくなるわけだが。。。)
計算して確認する
以下の例を見てほしい。
例えば値のリスト $[10, 12, 14]$ を考えると、平均 $\mu = 12$、分散は
$$
\sigma^2 = \frac{1}{3}\Bigl((10-12)^2 + (12-12)^2 + (14-12)^2\Bigr) = 4
$$
となり、標準偏差は $\sigma = \sqrt{\sigma^2} = 2$ 。各値を標準偏差で割ると
$$
\left[\frac{10-12}{2},\ \frac{12-12}{2},\ \frac{14-12}{2}\right] = [-1, 0, 1]
$$
のように「ばらつきが 1 に揃った」形になる。SDPA で $\sqrt{d_k}$ で割るのも同じ発想で、内積スコアの分散が次元数に比例する性質を利用し、標準偏差(平方根)で割ってスケールを整えている。
Python実装
import torch
import torch.nn.functional as F
def scaled_dot_product_attention(q, k, v, mask=None, dropout_p=0.0):
"""
q, k, v: (batch, n_heads, seq_len, d_k)
mask: (batch, 1, seq_len_q, seq_len_k) # True=keep, False=mask
"""
#次元数を取得
d_k = q.size(-1)
# W_Q,W_Kからスコア計算 (batch, heads, seq_q, seq_k)
scores = torch.matmul(q, k.transpose(-2, -1)) / d_k**0.5
# マスク適用(Falseを極小値に置き換え)
if mask is not None:
scores = scores.masked_fill(~mask, float('-inf'))
# 正規化+ソフトマックス関数で、正規化されたアテンション重みを得る
attn = F.softmax(scores, dim=-1)
# ドロップアウト(必要に応じて)
if dropout_p > 0.0:
attn = F.dropout(attn, p=dropout_p)
# アテンション重み付きの値ベクトル(O)を計算
output = torch.matmul(attn, v)
return output, attn