Stacking - 計算編① -

1. はじめに

データコンペ界隈主導で、数%の精度を高める手法としてstacking・blendingが非常に流行っております(言わずもがなですが)。実務家として着目したいのは、数%の改善をする方法論だと思います。数%でチャリチャリ度合は全然違いますので、技術により利益貢献をするという目線で大変頼もしい手法です。StackingがKaggle主導で誕生した理由も、以下を覗くとうなずけます；

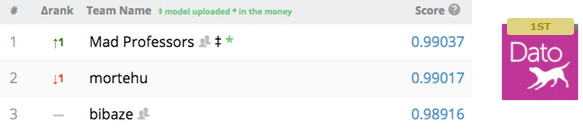
[http://goo.gl/T0OlsV より引用]
1位と2位の差が2bp(∝10^-4)とは全く驚きです。そこで本エントリーでは、Stackingの概要を整理した後、sklearnを使って実験を行い、Stackingにより得られる示唆を考察してみたいと思います。

2. Stackingとは

実のところ、何が正しいのか不明瞭なのですが、[4]を参照し解釈すると視点としては以下が挙げられると考えています；

• Subsamplingによりデータへの過適合を防ぐ(K fold)

• 観測したfeature(Design Matrix)は離散値 or 連続値で、モデルに通すことでDesign Matrixをアグリゲーションするだけでなく、featureをスムージングし、さらにfeature間の非線形性をモデル出力値(=meta feature)に反映させる

この中で、一番のメリットは後者ではないかと考えており、この3つに関し第2章で定性的に考察し、第8章では定量的な観点で再考します。なお、第3章で第2章にあげられた点をより具体的に整理した後、第4章で数値実験の概要・ねらいをまとめます。次に、第6章で取り扱ったデータについて簡単にふれ、結果を踏まえ、最終章で再度、Stackingについて考察してみたいと思います。

3. Stackingの利点

3.1 Subsamplingによりデータへの過適合を防ぐ

これは[4]で指摘されている通り

[http://goo.gl/MrV6qF より引用]

緑の決定境界を取得してもうれしくなく、黒が皆さんのご所望の結果だと思います。

3.2 Design Matrixのアグリゲーション

Stackingをする前と後で変わるのは、featureとして観測されたベクトルを直接用いるのか、モデルで変換されたベクトルを新たなfeatureとして使用する、という点だと思います。この際、新たなfeatureをmeta featureと呼ぶようです。
まとめると、変化前は

\begin{eqnarray}
\text{$X$ : Design Matrix, [n×d]} \\
\text{n : レコード数, d : feature次元数} \\
\end{eqnarray}

変化後は、

\begin{eqnarray}
\text{$\widetilde{X}$ : Transformed Design Matrix, [n×m]} \\
\text{n : レコード数, m : stackingで使用したモデル数} \\
\end{eqnarray}

Transformed Design Matrixの作り方がStackingと呼ばれる箇所なのですが、[4]をよく読んで下さいw。以下引用[4]、

Let’s say you want to do 2-fold stacking:

• Split the train set in 2 parts: train_a and train_b
• Fit a first-stage model on train_a and create predictions for train_b
• Fit the same model on train_b and create predictions for train_a
• Finally fit the model on the entire train set and create predictions for >the test set.
• Now train a second-stage stacker model on the probabilities from the first-stage model(s).

一般に、featureの次元dとStackingに使うモデル次元のmはd >> mですから、計画行列のサイズを大きく削減したことになります。

3.3 featureをスムージング

今、二値分類の問題を解きたいとします。予測モデルはSVMでもLRでもよく、(feature, ture label, predict label)となるはずです。この時、予測したラベルの確率を新たなfeatureとして使うという発想です。確率は[0,1]の値をとる正の実数ですから、離散値から連続値にスムージングされたことになります。離散値でない連続値の場合でもこの手法は有効ですので、生データが離散値・連続値の場合でも使用可能な手法という観点でも、使いやすい手法です。具体的な出力は下記の$\tilde{x}_i$です。

\begin{eqnarray}
f_i(X) = \tilde{x_i} \\
\text{$\tilde{x}_i$ : meta feature, i=1, ... , m} \\
\text{$dim(\tilde{x}_i)=n$} \\
\widetilde{X} = (\tilde{x}_1, \tilde{x}_2, ..., \tilde{x}_m) \\
\text{$X$ : Design Matrix, [n×d]} \\
\text{$f_i$ : Stackingに使用したi番目のモデル}
\end{eqnarray}

3.4 feature間の非線形性をモデル出力値に反映させる

さて、feature間の非線形性という話は常にデータ分析での悩みどころです。生データを非線形変換して線形データとして扱いやすくした後、処理する方法もあります。Stackingは、生データをモデルに投入し出力値をmeta featureとして扱う方法で、モデルに投入している箇所が非線形変換に相当していると考えられます。

4. データ

[9]の第3章参照。

5. scikit-learnを使ったねらい・実験概要

ねらいは明確で、数%の改善をする方法なのかを確認する点で、以前実験[9]した値をアウトパフォーム出来るかを比較してみます。
実験概要ですが、次のような2-Levelのアンサンブル学習を行いました。ただし、一般的には1-Levelで複数の学習器を使いますが、今回はSVMのみです。
0-Level : Feature Transformation by GBDT, [9]
1-Level : Stacked by SVM
2-Level : Final Prediction by LR
1-Levelの話は[7]、[8]が詳しいです。
使用したコードです、https://goo.gl/UNvhwL

6. 結果

	accuracy	precision	recall	f-value
Stacking	8.60E-01**	9.33E-01	8.88E-01	9.10E-01**
GBDR + LR	8.55E-01	9.23E-01	8.90E-01**	9.06E-01
LR	7.58E-01	9.72E-01**	7.70E-01	8.59E-01
注)
accuracy = float(TP + TN) / float(TP + FP + FN + TN)
precision = float(TP) / float(TP + FP)
recall = float(TP) / float(TP + FN)
f-value = 2.0 * precision * recall / (precision + recall)
TP : True Positive
TN : True Negative
FP : False Positive
FN : False Negative

7. 考察

数%の改善ができたかという観点では、このデータセットではマチマチという結果でした。以前の実験[9]自体がデータをGBDTで非線形変換し、LRしています。今回の実験で異なるのは、①Design Matrixの次元を削減②featureをスムージング、の2点で、これらが寄与しています。ただし、全体が改善していない事を鑑みると、あまり効果はなかったと・・・。他方、さらなる実験として2つをすべきだと考えています。1-Levelの設定で複数の学習器を実行していないという点と、生データをGBDTではなく、生のままか異なる手法を用いて0-Levelを設計できるなとも思っています。
1-Levelの設定について[9]の筆者は以下の様に述べています；

• Patience. Don't get lost in premature optimization with ensembles.
• The higher the stacking level, the shallower the models need to be

また、以下のような設計をStackNetと呼ぶそうです。

• A weighted rank average of multi-layer meta-model networks (StackNet).

この辺りはもしかすると、1-Levelから2-Levelでの線形和をNNで使う線形変換(W)を求めるBackPropagationの様に、教師あり学習として定式化出来るかもしれないとも思っています。
という事で、今回は以上です。次回以降はさらなる実験をする為に、1-Levelの設計テンプレートを作ろうかなと思っています。

8. 参考文献

[1] Wolpert, David H. Stacked generalization, Neural Networks, 5(2), 1992.
[2] Ting, etc, Issues in Stacked Generalization, Journal of Artificial Intelligence Research, Vol 10(1), 271-289, 1999.
[3] KM. Ting, etc, Stacked Generalization: when does it work?, IJCAI, Vol2, 866-871, 1997
[4] KAGGLE ENSEMBLING GUIDE, http://goo.gl/MrV6qF.
[5] Predicting a Biological Response. https://goo.gl/Q3jom5, Kaggle Data Competition, 2012.
[6] Dato Winners' Interview: 1st place, Mad Professors, http://goo.gl/T0OlsV, Kaggle Data Competition, 2015.
[7] puyokwの日記, stacked generalization, http://goo.gl/1917RD
[8] J.Sill, etc, Feature-Weighted Linear Stacking, arxiv, 0911.0460.
[9] Gradient Boostingについて - Scikit-Learnを使ったfeature transformation(GBDT + LR vs LR) - http://goo.gl/qwhpbJ