1. はじめに
Noise-Contrastive Estimation(NCE)とは、分配関数を陽に書き下せるものの数値積分が困難な場合や、MCMCではものすごく時間がかかる場合に対処するパラメータ推定方法の事です。物理で言えば1次元Ising Modelは転送行列を使って紙と鉛筆で計算できますが、2次元以上は解析解がありません(2次元で外場が無い場合は出来るそうです)。そこで、従来はMCMC等が用いられていましたが、異なる方法論としてNCEが提唱されました([M.U.Gutmann, etc]の論文中では画像処理)。
自然言語処理ではsoft-max関数で確率を計算する際よく用いられますが、NCEではその分母を直接計算するのではなく、分母をパラメータとして扱うため、モデルパラメータ + 分母が求めるパラメータとなります。有名な応用として[A.Mnih, etc]が挙げられます。
MCMCは分配関数を数値計算で近似しますが、NCEは目的関数を近似して計算します。ただし理論的に、NCEは一定条件の下、漸近的にMLEと類似した振舞をするという理論解析があり、安心できる推定方法です(難点はありますが)。
-
MLEの振る舞い
- 一致性を持つ
- 漸近正規性を持つ
- 推定量が漸近正規性を持つことの良い側面は、推定量の検定が出来る点にあると思います
- 例えば、χ二乗検定が出来るのは、検定統計量の漸近分布がχ二乗に一致するからで、所謂1-αはχ二乗のパーセンタイル点です
- 漸近有効性を持つ
- 漸近有効性という概念は、パラメータを分布として推定する際、結果の安定性を議論する量(推定量に関する分散の上限バウンド)です。
- 分散が小さいほうが結果が安定します。MLE > BE(Bayes Estimator)の順にバウンドがタイトだったはずです
- 参考
- [D.Sun, F.Xiao]にまとまっています。
-
NCEの振る舞い
- 一致性を持つ
- 漸近正規性をもつ
-
MLEとNCEの分散が近似的に一致する
- 分配関数が求まる場合に成立するものの、NCEを使うので現実的にはあり得ません(なので、近似的に成り立つという事です)。
- NCEは分配関数が直接的に計算できないこその推定方法なので、MLEとNCEの分散が近似的にも一致することはありません。
- ここでは、分配関数が求まると考えるならば、MLEとNCEの分散が近似的に一致するという話です。
- noiseサンプルが十分大きい場合に成立します
- 分配関数が求まる場合に成立するものの、NCEを使うので現実的にはあり得ません(なので、近似的に成り立つという事です)。
本投稿では、まずNCE問題を定式化した後、得られる推定量を性質(一致性・漸近正規性・MLEとの関連)を整理します。第5章にて、[M.U.Gutmann, etc]で例として挙げられている多変量正規分布のPrecision Matrixを推定する問題をやってみます。最後に考察を兼ねたまとめを記しておきます。
証明は[SlideShare]を参照して下さい(実は一番時間がかかった)。
2. NCE問題の定式化
\begin{eqnarray}
J_T(\mathbf{\theta})) &=& \sum_{t=1}^{T_d + T_n} C_t lnP(C_t=1 | \mathbf{u}_t;\mathbf{\theta}) + (1-C_t)lnP(C_t=0 | \mathbf{u}_t;\mathbf{\theta}) \\
&=& \sum_{t=1}^{T_d} lnP(C_t=1 | \mathbf{u}_t;\mathbf{\theta}) + \sum_{t=1}^{T_n} lnP(C_t=0 | \mathbf{u}_t;\mathbf{\theta}) \\
&=& \sum_{t=1}^{T_d} ln h(\mathbf{x}_t;\mathbf{\theta}) + \sum_{t=1}^{T_n} ln \left\{ 1 - h(\mathbf{y}_t;\mathbf{\theta}) \right\}
\end{eqnarray}
,where
\begin{eqnarray}
\mathbf{u}_t=\left\{ \begin{array}{ll}
\mathbf{x}_t & (\mathbf{u}_t \in {\cal X}) \\
\mathbf{y}_t & (\mathbf{u}_t \in {\cal Y})
\end{array} \right. \\
\end{eqnarray}
\begin{eqnarray}
P(C=1 | \mathbf{u};\mathbf{\theta}) &=& \frac{P(C=1)P(\mathbf{u} | C=1;\mathbf{\theta})}{{\cal Z}} \\
&=& \frac{p_m(\mathbf{u};\mathbf{\theta})}{p_m(\mathbf{u};\mathbf{\theta}) + \nu p_n(\mathbf{u})}, \\
&=& \left\{ 1 + \nu \frac{p_n(\mathbf{u})}{p_m(\mathbf{u};\mathbf{\theta})} \right\}^{-1} \\
&=& \frac{1}{1 + \nu * exp\left\{ lnp_n(\mathbf{u}) - lnp_m({\mathbf{u};\mathbf{\theta})} \right\}} \\
\Leftrightarrow h(\mathbf{u};\mathbf{\theta}) &=& r_{\nu}(G(\mathbf{u};\mathbf{\theta})). \\
\\
P(C=1 | \mathbf{u};\mathbf{\theta}) &=& h(\mathbf{u};\mathbf{\theta}), \\
G(\mathbf{u};\mathbf{\theta}) &=& lnp_m(\mathbf{u};\mathbf{\theta}) - lnp_n(\mathbf{u}), \\
r_{\nu}(\alpha) &=& \frac{1}{1 + \nu exp(-\alpha)} \\
lnp_m(\mathbf{u};\mathbf{\theta}) &=& lnp_m^{0}(\mathbf{u};\mathbf{\theta}) + c \\
& & \text{c is normalized constant }, c=ln({\cal Z}) \\
& & \text{$p_m^{0}$ is true model}. \\
\\
P(C=0 | \mathbf{x}_t;\mathbf{\theta}) &=& \frac{P(C=0)P(\mathbf{u} | C=0;\mathbf{\theta})}{{\cal Z}} \\
&=& \frac{\nu p_n(\mathbf{u};\mathbf{\theta})}{p_m(\mathbf{u};\mathbf{\theta}) + \nu p_n(\mathbf{u})}.
\end{eqnarray}
- データを下記の様に定義する
- $X \in R^{p \times T_d}$ : 観測データ
- $Y \in R^{p \times T_n}$ : ノイズとして観測したデータ。ただし、$T_n = \nu T_d$でノイズデータの分布は既知
- $p$ is feature dim
- NCEにおける最適化問題
\begin{eqnarray}
\hat{\mathbf{\theta}}_T &=& \ argmax \frac{1}{T_d} {\cal L}(\mathbf{\theta}) \\
\Leftrightarrow \hat{\mathbf{\theta}}_T &=& \ argmax J_T(\mathbf{\theta}) \\
\Leftrightarrow \hat{\mathbf{\theta}}_T &=& \ argmax \frac{1}{T_d} \sum_{1}^{T_d} ln \left\{ h(\mathbf{x}_t;\mathbf{\theta}) \right\} + \frac{\nu}{T_n} \sum_{1}^{T_n} ln \left\{ 1 - h(\mathbf{y}_t;\mathbf{\theta}) \right\}
\end{eqnarray}
3. NCEの条件
- $J(\theta)$は$lnp_m$が真のモデル($lnp_d$)で最大値をとる
- $p_d$が非ゼロの分布である時、常にノイズ分布$p_n$も非ゼロの分布をもつ
- データを観測したとき、必ず真の分布から発生したサンプルとノイズ分布から発生するサンプルが存在する
上記の条件も重要ですが漸近的($\nu \rightarrow \infty$)にMLEと同様の振る舞いするには別の条件が必要です。
大まかには
- $J_T(\mathbf{\theta})$のHessianが$T_d \rightarrow \infty$の時にある行列に確率収束し、
- NCEにおける$J_T$のHessianとMLEにおける対数尤度のHessianを比較する際に使います。
- つまり、MLEとNCEの分散を比較する際に使う量です。
- さらに分配関数が求まる状況の時($\nu \rightarrow \infty$)、NCEで計算した推定量はMLEにおける推定誤差(=$\mathbf{\theta} - \mathbf{\theta}^*$)と同じ分布(漸近正規性)を持つ
という事になります。
4. NCEの性質
- Theorem2(一致性)
\begin{eqnarray}
\hat{\mathbf{\theta}}_T &\rightarrow& \mathbf{\theta}^* \text{ in probability} \\
&& \text{where, } \mathbf{\theta}^* \text{is optimal}
\end{eqnarray}
SlideShareのP9を参照してください
- Theorem3(漸近正規性)
\begin{eqnarray}
\sqrt{T_d} (\hat{\mathbf{\theta}}_T - \mathbf{\theta}^*) &\rightarrow& N(\mathbf{0}, \Sigma)
\end{eqnarray}
SlideShareのP14を参照してください。ちなみに、Theorem3に至るにはLemma11, Lemma12, Lemma13, Lemma14が必要となり、詳細はP10～P13に記載してあります。
- Corollary5(MLEとNCEの分散が近似的に一致)
\begin{eqnarray}
\Sigma &=& I^{-1} - I^{-1} E[\mathbf{g}] E[\mathbf{g}^t] I^{-1} \\
&& \text{where, $I$ is Fisher Information Matrix.} \\
\end{eqnarray}
proof
\begin{eqnarray}
P_{\nu}(\mathbf{u}) &=& \frac{\nu p_n(\mathbf{u})}{p_m(\mathbf{u};\mathbf{\theta}) + \nu p_n(\mathbf{u})} \\
&=& \frac{p_n(\mathbf{u})}{\frac{1}{\nu} p_m(\mathbf{u};\mathbf{\theta}) + p_n(\mathbf{u})}. \\
\lim_{\nu \to \infty} P_{\nu}(\mathbf{u}) &=& 1 \\
\end{eqnarray}
From theorem3 and Lemma10,
\begin{eqnarray}
\Sigma &=& I^{-1} - (1+\frac{1}{\nu})I^{-1} E[P_{\nu} \mathbf{g}] E[P_{\nu} \mathbf{g}^t] I^{-1} \\
\mathbf{g}(\mathbf{u}) &=&\nabla_{\mathbf{\theta}} lnp_m(\mathbf{u};\mathbf{\theta}) |_{\mathbf{\theta}=\mathbf{\theta}^*}
\end{eqnarray}
Therefore, as $\nu$ goes infinity
\begin{eqnarray}
\Sigma &=& I^{-1} - I^{-1} E[\mathbf{g}] E[\mathbf{g}^t] I^{-1} \\
\end{eqnarray}
もし、分配関数がパラメータではない場合、$E[\mathbf{g}]$はゼロなので、MLEの分散と一致する。
5. シミュレーション例
- 問題設定
- 真のモデル:多変量標準正規分布
- $ln p_d(\mathbf{x}) = -\frac{1}{2} \mathbf{x}^t \Lambda^* \mathbf{x} + c^*$
- $c^* = -\frac{1}{2} ln | (\Lambda^{-1})^* | - \frac{n}{2}ln(2\pi)$
- $\Lambda^* = \Sigma^{-1}$
- $\Lambda^*$ = np.random.randn(3,3) / 10
- 推定モデル
- $ln p_m(\mathbf{x}) = ln p_m^0(\mathbf{x}) + c$
- $p_m^0(\mathbf{x}) \sim N(\mu, \Lambda^{-1})$と仮定
- $p_n \sim N(\mathbf{0}, diag(1,1,1))$と仮定
- 推定パラメータ
- $\mathbf{\theta} = \mu, \Lambda, c$
- 真のモデル:多変量標準正規分布
- 見どころ
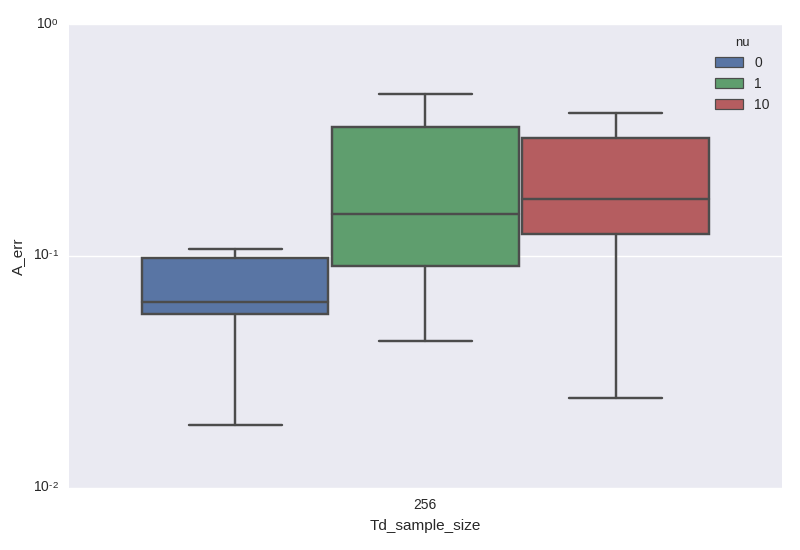
- $\nu$を大きくすると推定量の分散が小さくなるはずので、それを確認する
- 結果
- 今回、PrecisionMatrixは$3 \times 3$の行列で、推定するのは、その各々の成分
- Errは$\frac{1}{9}\sum_{i,j} (\Lambda_{i,j}^{*} - \Lambda_{i,j})^2$として計算
- $\nu=0$がMLE
- $\nu$を大きくするとNCEで推定したPrecisionMatrixの分散が小さくなっている事が確認できます。
- 一方で、中央値がさがってない・・・
- ちなみに、まとめでふれますが$\nu$を大きくしすぎると$J_T$が発散してしまいます
6. まとめ
5.1 NCEが魅力的に映る
繰り返しになりますが、NCEによる推定量が①一致性を持つ②漸近正規性をもつ③MLEとNCEの分散が近似的に一致するという性質が非常に望ましいことを述べさせていただきます。
6.2 ノイズサンプルは大きくし過ぎない
注意といいますが、$\nu$を大きくし過ぎると死にます。理由は次の通りです；
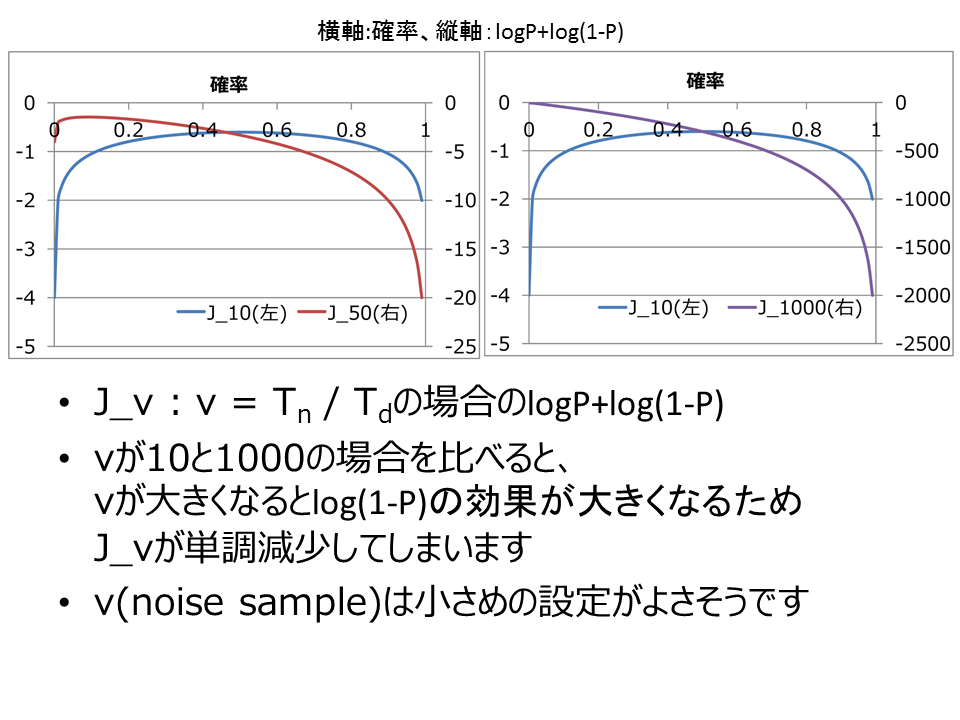
一応これが正しいことも確認しておきます。最大化したい目的関数は以下でした；
\frac{1}{T_d} \sum_{1}^{T_d} ln \left\{ h(\mathbf{x}_t;\mathbf{\theta}) \right\} + \frac{\nu}{T_n} \sum_{1}^{T_n} ln \left\{ 1 - h(\mathbf{y}_t;\mathbf{\theta}) \right\}
簡単の為、ln{h}とln{1-h}が等しい値をとると仮定します。$T_n=\nu T_d$でしたので、$\frac{1}{T_d}=\frac{\nu}{T_n}$です。つまり、足し上げる回数が多い方が全体に占める比重が支配的になります。結果、$\nu$が大きい場合、目的関数はノイズ分布からのサンプルに影響されます。図でいうと紫(J_1000)をみると一目瞭然で、ノイズ分布からのサンプルが強く、単調減少しているように見えます。
ですので、$\nu$は大きくし過ぎないほうがいいと思います。計算していたら、紫のように発散しましたw
6.3 レアイベント予測に関する最適化問題への応用
異なる視点としてNCEはクリック予測など、レアイベント予測に関する最適化問題を解くことに相性が良い方法なのではないかと考えています。それは、目的関数 = 真の分布からのサンプル + ノイズ分布のサンプルと分解しているからです。通常、レアイベント予測では観測できるラベルデータが少ないか、偏りが強いためパラメータ推定が困難です（ViewThroughClick、ClickThroughConversionもありますね）。正則化・不均衡データ・ハイパーパラメータ調整などにより処理するのが通常かと思います。私も訓練データを不均衡データとして扱い、パラメータ学習に使うサンプルをある経験分布に従いサンプルしたり、ある基準で閾値を決めて訓練データを限定したりします。この限定という操作は目的関数を設計していないのものの、NCEにより目的関数の設計をすることで、限定を理論的に整理できるかもと最近考えています。恐らく、NCEでのノイズ分布からのサンプル = 不均衡データでの経験分布に従うサンプル、という対応がある気がしています。
明日は、@antimon2さんによる「AdaBoostについて実験した結果」です、お楽しみに!
参考文献
[M.U.Gutmann, etc] Noise-Contrastive Estimation of Unnormalized Statistical Models, with Applications to Natural Image Statistics, Journal of Machine Learning Research, 13, 307-361, 2012
[A.Mnih, etc] Learning word embeddings efficiently with noise-contrastive estimation, Advances in Neural Information Processing Systems 26, NIPS, 2013
[D.Sun, F.Xiao] Likelihood Theory with Score Function
[SlideShare] Note : Noise constastive estimation of unnormalized statictics methods