パズドラの初期盤面生成アルゴリズムを暴く

「パズドラの初期盤面ではドロップが揃わないようになっている」
本当に ?

tl;dr

3DS版パズドラであるパズドラZを用いて検証・解析を行いました。
パズドラZでの初期盤面生成処理は以下のようになっています。

各マス、ランダムにドロップ種類を決める (この時点ではドロップが揃っている可能性がある)
左下のドロップから順に見ていく。今見ているドロップをXとする。Xを含むコンボがあるならば、Xを火, 水, 木, 光, 闇, 回復の順に変えていき、Xを含むコンボが $1$ つもなくなった時点でXに対する処理を終了とし、次のドロップに行く。ただし、この際ダンジョンの指定色(3色ダンジョンなど)により生成されるべきでない種類への置き換えは試さず。その色はスキップする。色を全部試してもコンボが解消されなかったら、Xは最後に試した色のままにして次のドロップに行く。
なお、「左下のドロップから順に」は以下の2通り考えられるが、これらは全く同じ結果を生み、区別する意味はない。(実際は右になっている)

したがって、回復含めて $4$ 色 (以下) のダンジョンでは稀に初期盤面でドロップが揃っていることがあります。
また、初期盤面ではドロップは火, 水, 木, 光, 闇, 回復の順に多く生成されます。例えば火,水,木,回復のダンジョンでは、最も出やすい火ドロップが最も出にくい回復ドロップより平均で $1.5$ 個程度多く出ます。

また、例えば(回復込みで) $4$ 色のダンジョンでは上記の方法で生成され得る初期盤面 (=揃ったドロップの存在しない盤面) が $1.4 \times 10^{17}$ 通りあるのに対して実際にはそのうち $65536$ 通りしか出てきません。どういう仕組みかは後述。

パズドラの概要

パズドラ (パズル＆ドラゴンズ) では通常、6x5のグリッド状の盤面に以下の6種類のドロップが配置されます。

火(赤)
水(青)
木(緑)
光(黄)
闇(紫)
回復(ピンク)

以下はドロップ配置の例です。

バトルでは同じ種類のドロップを縦または横に $3$ つ以上並べて消す「コンボ」¹を使って攻撃を行うのですが、このパズルの詳細については本筋からそれるのでこの記事では省略します。

初期盤面生成

パズドラでは戦闘開始時にランダムな盤面が生成されます。
しかし、全ての盤面が生成され得るわけではありません。少し遊んでいると、初期盤面にはコンボが発生する箇所が出てこないことが分かります。
では、コンボが発生しないような盤面の生成処理はどのように行われているのでしょうか ?
当初、普通は以下のような処理をするものだと思っていました。

説A (揃わなくなるまで再生成)

全てのマスについて、6種類の中から独立かつ一様ランダムにドロップを決める
同じ種類のドロップが揃っている箇所がある限り、1.に従って盤面全体を生成し直す

しかし、後述しますがどうやらこれは誤りのようです。

先行研究

このツイートに、にる/HumanNil氏によるスマホ版パズドラの初期盤面生成アルゴリズムの調査結果がまとめられています。
これによると、どうやら以下のような処理が行われているようです。

説B (コンボ箇所を火から順に置換)

全マス適当にランダムにドロップを決める
盤面の左側(上から下からかは不明)からドロップを見ていき、コンボが発生している所を火, 水, 木, 光, 闇, 回復の順に置き換えていき、コンボが解消した時点で置き換えを停止する

これは、初期盤面には火ドロップが一番多く生成されると主張しています。「そんなバカな」と言いたいところですが確かめてみないことにはなんとも言えません。

検証

できれば今一番メジャーなスマホ版パズドラで検証したいのですが、「スタミナ」という邪悪概念が行く手を阻みます。
「統率力」と言ってみたり「ライブボーナス」と言ってみたり、ソシャゲはだいたい遊ぶとゲーム内で何か消費されるものです。
これでは重課金まっしぐらなので、買い切りソフトである3DS版パズドラ(パズドラZ)で実験することにしました。発売から $10$ 年経っていますが、スマホ版も同じ頃から存在しているのでひどい違いはないだろうと踏んでのことです。

盤面画像の採取

盤面生成のアルゴリズムの仮説を検証するにはそれなりに多くの盤面を生成してデータを取る必要があります。人間の手でやると日が暮れてしまう以上に単調すぎて気が狂いそうなので自動化したいところです。
ありがたいことに3DSにはcitraというPC向けエミュレータが存在しています。
ゲームソフトのファイル(拡張子.cia)は、CFW(Custom Firmware)の入った実機でカセットから吸い出せます。決して怪しいところから取ってきてはいけません。
このエミュレータ、スクリプトやAPIでボタン/タッチ入力するような機能はなさそうなので、Windowsのレベルでマウス操作を自動化してしまえとなりました。そのためのツールがAutoHotkeyです。更に、画面のスクリーンショットを取れるコマンドラインツールnircmdを導入して、AutoHotkeyのスクリプトから呼び出すことにしました。
これにより、「ダンジョンに入って初期盤面が見えたらスクリーンショットを取って抜ける」というのをひたすら繰り返す自動機構ができました。
この際つまづいた箇所は以下です :

AutoHotkeyスクリプトからのキーボード入力がcitraには効かない
citraがもっと下のレイヤでキー入力をキャプチャしているのかなと思ったり。マウスクリックは効いたので全部そっちでやることにしました。
AutoHotkey上でのスクリーンショット
標準ではそのような機能はなく、検索すると出てくるGdipとやらのライブラリもメンテナンスが止まっていてAutoHotkey v2の最新バージョンだと動きません。面倒なので先述の通りスクリーンショットを取るコマンドを呼び出す方式にしました。

citraのエミュレーション速度を200%(2倍速)などにすればスピードアップができ、毎時 $450$ サンプルほどが取れるようになります。
丸一日回しておけば $10000$ サンプル集まります。

盤面画像の処理

次にスクリーンショットからドロップ配置を読み取る必要があります。
機械学習は分からないので力技で判別します。
基本的には、ドロップ内の色平均(RGBごとの平均)をとったものの色相を見れば良いです。以下に各種類のだいたいの色相($0$ 以上 $1$ 以下)を載せておきます

火(赤) : 0.02
水(青) : 0.58
木(緑) : 0.41
光(黄) : 0.14
闇(紫) : 0.82
回復(ピンク) : 0.90

曲者なのがZドロップ(下画像で輝いているドロップ)です。
Zドロップは攻撃力3倍のドロップなのですが、こいつ周りにキラキラしたのをまき散らしやがります。画像でもZドロップの右や右上の火ドロップがピンクっぽくなったり下の木ドロップが青緑っぽくなったりしているのが分かります。

特にキラキラにまみれた木ドロップとキラキラにまみれた水ドロップは、色相の大小(?)が一貫しておらず判別ができません。
そのため以下のような方法を取りました。

Zドロップが含まれない画像を手動で $100$ 枚ほどピックアップする
1.の画像を読み込み、平均色の色相でドロップを自動判別し、各位置及び色についてドロップの画像を保存する。$100$ 枚もあれば全ての位置及び色についてドロップの画像が得られる。
ここで、各色でなく各位置及び色としたのは、後に行うドロップの一致判定が割と単純なピクセルごとの $2$ 乗誤差などなので、同じ種類のドロップでも場所が違うとわずかに画像に差異が出てしまい判別に影響を及ぼすためである
本データでドロップを判別するときは、対応する位置の各色のドロップの画像(2.で得られた)とピクセルごとの平均二乗誤差を求め、それが最小となる色をそのドロップの色とする。平均二乗誤差の数値的に判定が微妙なものを出力し、目視で確認したが誤りはなかった。

無理矢理感ありますが、動けば正義です。

仮説の検証

盤面生成のアルゴリズムの仮説が複数あったときに、検証結果がどれと整合するかを確かめるために以下のようなことをします。

盤面の特徴量を決める
例えば、$1$ つの盤面内の火ドロップの個数を特徴量にすれば説A(揃わなくなるまで再生成)と説B(コンボ箇所を火から順に置換)との区別に使えます。
C++による当該アルゴリズムのシミュレーションをし、実際のデータと合うか比べる

結果

試しに上の方法で、火水木+回復の$3$ 色ダンジョン(ドロップは回復を含めて $4$ 種類)であるシャングリラエリア妖精の森ステージ $3$ 妖精の宮殿に出入りして、合計 $49318$ 盤面取得しました。

解析1. ドロップ種類ごとの偏り

まず、説Bで特徴的な、$1$ つの盤面における各ドロップの平均出現頻度を見ます。

火 : 8.36205847763494 +- 0.008351056540703677
水 : 7.59708422888195 +- 0.008638541912877344
木 : 7.129384808791921 +- 0.008687017449026807
回復 : 6.9114724846911875 +- 0.0088865391659797

明らかに均等ではなく、火ドロップが多く出ています。まじか...
説A(揃わなくなるまで再生成)では全て均等に(7.5個ずつ)出るはずなので、矛盾しています。
また、他に「コンボがあったらバトル中と同様それを消して上からドロップを降らせることを繰り返す」という説も同様にドロップの種類に関する対称性があるのでこの結果に矛盾します。
では説Bとは本当に乖離しないのかというと... ?
説BのC++のシミュレーション($10^9$ サンプル)との対応なし $t$ 検定の $t$ 値は以下の通り (形式 : エミュレータの結果の結果の平均/シミュレーションの結果の平均 t=t値)

火 : 8.36206/8.34403 t=2.15484
水 : 7.59708/7.59656 t=0.0606562
木 : 7.12938/7.12041 t=1.02932
回復 : 6.91147/6.93899 t=-3.09055

有意差が出てしまった...
ただ、説Aなどよりは遥かに合致しているので、説Bまたは説Bのマイナーチェンジが正しいのではないかと考えて続行します。

解析2. 置換処理の順序

説Bが正しいとして、にる氏の調査では左列から置換処理が行われていることは分かるが、上からか下からかは分からないということだったので、置換処理の順番を特定したいと思います。(ついでに左から処理が行われていることを確認したいと思います)
以下の量を特徴量にとることを考えます :

$\mathrm{RXX0} : $ 縦方向の連続した $3$ ドロップであって、上から順に火XX(Xは火以外)という並びのものの数
$\mathrm{RXX1} : $ 縦方向の連続した $3$ ドロップであって、下から順に火XX(Xは火以外)という並びのものの数
$\mathrm{RXX2} : $ 横方向の連続した $3$ ドロップであって、左から順に火XX(Xは火以外)という並びのものの数
$\mathrm{RXX3} : $ 横方向の連続した $3$ ドロップであって、右から順に火XX(Xは火以外)という並びのものの数

もし処理が左から行われていたとすると、横方向のコンボの解消の際に「左から順に火XX」のパターンが生成されやすくなるので、本来左右の対称性から等しくなるなるはずの $\mathrm{RXX2}$ と $\mathrm{RXX3}$ が $\mathrm{RXX2} > \mathrm{RXX3}$ となるはずです。
同様に処理が上からならば $\mathrm{RXX0} > \mathrm{RXX1}$ , 下からならば $\mathrm{RXX0} < \mathrm{RXX1}$ となるはずです。
以下がエミュレータの検証結果です。

RXX #0 : 0.9072346810495154 +- 0.003929124710445291
RXX #1 : 1.2365667707530719 +- 0.004413960495543689
RXX #2 : 1.346891601443692 +- 0.004580549668363306
RXX #3 : 1.0139097286994607 +- 0.004106158090058048

この結果から、処理は確かに左から、そして下から行われていることが分かります。
シミュレーションとの比較は以下の通り。

RXX #0 : 0.907235/0.906775 t=0.117525
RXX #1 : 1.23657/1.23315 t=0.772916
RXX #2 : 1.34689/1.34728 t=-0.0853807
RXX #3 : 1.01391/1.0175 t=-0.872494

こちらは合致しています。
ここで、(冒頭tl;drの項に載せましたが) 「左から、下から」なら以下の $2$ パターンのどっちなんだという疑問が生じます。(これ以外の可能性もないとは言えませんが正気の実装をしていたらこの $2$ つのどちらかでしょう)

実は、同じ盤面から処理を始めると、この $2$ つのどちらの順序で処理をしても常に同じ結果の盤面になるので、これらは区別不能です。

証明

上の $2$ つの処理順序パターンをそれぞれ順序A, 順序Bとする。
例えば下図で赤で囲まれたドロップ(Xとする)を今見ているとする。Xを見終わったときにXがどの種類になっているかは緑で囲まれたドロップがその時点でどうなっているかのみに依存する。
ここでオレンジの部分のドロップは順序AでもBでも今までにまだ見られていないドロップなので、順序A, Bの間で同じである。従って「白色部分の種類がその時点で順序A, B間で同じならば、Xは順序A, B間で同じ種類のドロップに変化する」が成立する。
白色部分のドロップは順序AでもBでも既に見終わっていて、$1$ 度見終わったドロップの種類は最後まで変わらないので、「白色部分のドロップの最終的な種類が順序A, B間で同じならば、赤で囲んだドロップの最終的な種類も順序A, B間で同じ」が成立し、数学的帰納法が回る。

というわけで無事置換処理の順序を特定することができました。

解析3. 初期盤面でのコンボ

にる氏の元ツイートに対するリプでも指摘されていましたが、説Bには問題があります。
回復込みで $4$ 色のダンジョンでは、あるドロップの周り4方向に相異なる $4$ 色が $2$ 個ずつ連なっている場合、置き換えを全色試してもコンボが解消されないのです。
これに対しては今回の検証で決定的な結果が得られました。なんと初期盤面でドロップが揃ってしまっている例が見られたのです。
以下はその例です。上から $3$ 行目、左から $5$ 列目の火ドロップはもともと木ドロップだったと考えられます。

回復込みで $4$ 色のダンジョンにおける $49318$ 回の生成で $5$ 回そのような例が発生しました。そして揃っていたのは毎回ハートだったのです。
つまり、「ハートまで試して全部だめだったら仕方ないから諦めてハートのままにして次に行く」ということをやっている可能性が高いのです。
この時、ハートのコンボが上または右方向に伸びていれば、以後そのドロップが再度置き換えられてコンボは解消されますが、下または左方向に伸びていた場合、そのコンボは解消されることなく初期盤面に入り込んでくるというわけです。

解析4. 謎の重複

以上から、冒頭tl;drの項に書かれているような初期盤面生成アルゴリズムである可能性が高いと推定できました。
一件落着かと思われたのですが、得られたデータを解析していると奇妙なことに気が付きます。
得られた約 $49318$ 盤面から全く同じ盤面が出ていないか探すと...

$14826$ 個の重複があったのです。(正確には、得られた盤面から重複を除くと $14826$ 個減ってしまうという意味です)
$4$ 色を $5 \times 6$ の $30$ マスに配置する方法は $1.2 \times 10^{18}$ 通り、そのうちコンボが無いのは $1.4 \times 10^{17}$ 通りあります。上記のコンボ解消方法によって各盤面が生成される確率が多少偏ったところで $50000$ 個のうち $14000$ 個も重複するなどあり得ないのです。

この重複度合いからシミュレーションで推定した結果によると、生成され得る盤面は全部でだいたい $65000$ 種類しかないということになります。
どうしてこんなことに...
私は以下のことを考えました

1. 盤面取得の自動操作の際、なんかのはずみに同じ盤面を $2$ 回連続で撮ってしまったのではないか ?

→ 得られたスクリーンショットを撮影時刻順に処理し、連続して同じ盤面が出る回数を数えたところ、$3$ 回だけだった。また、そのような $2$ 枚のスクリーンショットでは助っ人が異なっていたので本当にたまたまだと考えられる。つまり $\frac{1}{65000}$ を $50000$ 回やって $3$ 回当てたというだけである。

2. 乱数生成器が雑で、状態が $2^{16} = 65536$ くらいしかないんじゃないか ?

→ 数字が近くてもっともらしいのだが
1. 同じ盤面のスクリーンショットを見比べると、敵の種類や残りターン数(これもランダムであろうと思われる)が異なっている。もし敵と盤面を同じ乱数生成器で連続して生成していたと仮定すると敵も同じになっているはずである。
2. 盤面生成の最初のステップで盤面全体をランダムに決める際、盤面のどこかの角から縦横どちらかの方向で順にドロップを決めていると仮定すると、乱数生成器の状態が少ないならば「Aの1~5列目とBの2~6列目が一致」や「Aの1~4行目とBの2~5行目が一致」となるような盤面の組 (A, B) が(その後のコンボ解消で乱される可能性を考えても)それなりの割合で発生するはずだが、そのようなものは $1$ つもなかった。

ことから可能性が低いと考えた。

3. 乱数生成器はちゃんとしているが、与えられるシードがなんらかの原因で $65000$ 通りくらいしかないのではないか ?

→ 2.の項に書いてある問題のうち2.は解決するが、依然として1.の問題は残る。とはいえ、敵と盤面に別シードの乱数生成器を用いていたり、両者の生成の間にシードを与えていたりという可能性から、あり得る話ではある。

4. エミュレータになんらかの原因(提供する時刻や乱数が雑など)があるんじゃないか

→ 実機で手動で $15$ 盤面生成したところ、うち $10$ 盤面がエミュレータで生成された約 $35000$ 種類の盤面のいずれかに一致した。そのため実機でも、生成され得る盤面はエミュレータと同じ約 $65000$ 種類の盤面のセットに制限されているものと思われる。

5. 実はゲームのリソースに $65000$ 通り埋め込まれていて、そこから選んでいるんじゃないか ?

→ .ciaファイル内の、ゲームリソースが埋め込まれているromfsと呼ばれる領域を展開して中身を見たものの、自分の技量ではあまりそれっぽいものは見つからなかった。$4, 5, 6$ 色ダンジョン全てについてデータがあるとすると合計 $1 \, \mathrm{MB}$ くらいにはなるので、あれば見つかりそうなものなのだが。(もっとも、パズドラZのゲームファイルは $700 \, \mathrm{MB}$ 以上あるのでごく一部と言えばごく一部である)

この原因の特定には難儀しました。

上に挙げた仮説のうち強い否定的な証拠が無いのは3と5です。5もあり得るのですが、これをやっていたとしたら何が起こってそんなことになったのか聞きたいようなひどい実装なので、3の線で考えます。何をシードにしているのでしょうか ?

リバースエンジニアリングパート

シードとしてよくあるのは時刻です。3DSのシステムで時間系の情報を取得するAPIは自分が調べた限り以下になります。

システム時刻を取得する、ptm:gets GetSystemTime
CPUの電源onからのクロック数を返す svcGetSystemTick (svc)

あとは本来暗号化通信に使われてそうな乱数を生成するAPIくらい :

ssl:c GenerateRandomData

svcGetSystemTick はシステムコール、それ以外はシステムコールを介したプロセス間通信によるAPIです。
エミュレータcitraはこれらのAPIを実装しているので、citraのソースを書き換えれば色々といじれます。
結論から言うと呼ばれていたのはsvcGetSystemTickのみでした。ただ、$1$ 秒間に $1000$ 回ほど呼び出されていてどの呼び出しが何に使われているのか分かりません。
そこで svcGetSystemTick に以下のような細工をしました。

戻り値の下位 $22 \, \mathrm{bit}$ を $0$ にしてしまう。(old)3DSのクロックは $268 \, \mathrm{MHz}$ なので、これによって生じる誤差は $16 \, \mathrm{ms}$ 程度に相当する。
更に戻り値の下から $29 \, \mathrm{bit}$ 目 (1-indexed) から上位も $0$ にしてしまう。これによって svcGetSystemTick の戻り値はだいたい $1$ 秒ごとにループすることとなる。

こうすると svcGetSystemTick が返す値は $64$ 通りしかなくなってしまいます。(ひどいですね)
この状態でパズドラZを起動すると、後者の細工によってループアニメーションが $1$ 秒おきにリセットされたりなどの軽微なグリッチが生じましたが、ダンジョンの出入りに支障はありませんでした。そして、試しに盤面生成をしてみると...

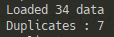
$34$ 盤面生成して $7$ 個重複したのです。前に生成した約 $50000$ の盤面のいずれかと一致したのが $7$ 個ではなく、$34$ 個の中で $7$ 個一致したのです。
つまり、パズドラZは svcGetSystemTick の結果をシードにしているということが分かりました。

ここから盤面生成アルゴリズムを解剖していきます。
実行コードを逆アセンブルして svcGetSystemTick に対応する命令 svc 0x00000028を探し、そこから乱数生成器のコードを見つけることができました。
使われている疑似乱数のアルゴリズムは以下のようになっていました。(これは手動で書き直したものです)

#include <stdint.h>
typedef uint32_t u32;

u32 rand_buf[8];
static inline u32 advance(size_t index) {
	rand_buf[index] = rand_buf[index] * (u32) 0x343FD + (u32) 0x269EC3; // MSVCのrandにも使われている有名パラメータ
}

void seed_rand() {
    rand_buf[0] = svcGetSystemTick() & 0xFFFFFFFF;
    for (size_t i = 1; i < 8; i++) {
        advance(0);
        rand_buf[i] = rand_buf[0] >> 16; // !
    }
    advance(0);
    // この後にrand_buf[0]を使って、メルセンヌツイスターと思われる別の乱数生成器の
    // 初期化が行われているが、盤面生成には使われていない。
}

// [0, 2^16)の範囲からランダムな整数を生成
u32 rand(size_t index) {
    advance(index);
    return rand_buf[i] >> 16;
}

$8$ つの独立した $\mathrm{mod} \hspace{4pt} 2^{32}$ 線形合同法の乱数生成器があり、seed_randはそれら全てを svcGetSystemTick を用いて初期化します。
ところが、よく見ると各乱数生成器に与えられる初期状態は $16 \, \mathrm{bit}$ 分しかありません。(// ! 部分)
これで謎が解けました。説3. 「乱数生成器はちゃんとしているが、与えられるシードがなんらかの原因で $65000$ 通りくらいしかないのではないか ?」が正しいのです。(線形合同法がちゃんとしているかは微妙だが、初期化部分以外にそんなにまずいところはなさそうである)
でもだからといって // ! の箇所で右シフトを何もしないと、初期化後に乱数生成器 $1$ を $1$ 回使った瞬間その状態が乱数生成器 $2$ と同じになってしまいます。

このコードは、$8$ つの乱数生成器を別々の用途に使おうというわけです。これは、盤面が同じなのに敵が異なる場合があることにも整合します。

ちなみに盤面生成は上のコードを用いて以下のようなアルゴリズムになっています。

// int board[16][16];
// int dungeon_n_allowed_drop_types
// int dungeon_allowed_drop_types[]

seed_rand();
for (int i = 0; i < 16; i++) for (int j = 0; j < 16; j++)
    board[i][j] = dungeon_allowed_drop_types[(rand(2) * dungeon_n_allowed_drop_types) >> 16];
for (int i = 0; i < 5; i++) for (int j = 0; j < 6; j++) {
    if (/* board[0...4][0...5]の範囲だけ見た時にboard[i][j]を含むコンボがある */) {
        for (int k = 0; k < dungeon_n_allowed_drop_types; k++) {
            board[i][j] = dungeon_allowed_drop_types[k];
            if (/* board[0...4][0...5]の範囲だけ見た時にboard[i][j]を含むコンボがない */) break;
        }
    }
}
// board[i][j] : 下からi番目、左からj番目のドロップの種類を表す整数 (0 <= i < 5, 0 <= j < 6)
// この後にZドロップの生成を行う

全ていままでの推定と合致しています。
なお、エミュレータによる結果で回復ドロップの出現頻度の $t$ 値の絶対値が $3$ を超えていた理由は分かりませんでした。試しに上の解析を元に、あり得る $65536$ 通りを全て生成してシミュレーションと比較すると、火ドロップの出現頻度に関して $t = 4.8$ などという事態に。
一般に(rand(2) * dungeon_n_allowed_drop_types) >> 16は一様に分布しないという話もありますが、dungeon_n_allowed_drop_types = 4 ではこの問題は起こりません。線形合同法の連続した出力が独立でないことに何か原因があるのかもしれません

完結

最初からアセンブリ読めば良かったじゃんという声が聞こえてきそうですが、だいたいどういうことをやってそうかの見当がついているのといないのとではアセンブリ読む難易度が大分違うはずなので今回のも悪くなかったんじゃないかなと思います。
HSV色空間, 統計, 自動操作, アセンブリ読解といろいろ学べたのでむしろ良かったかも。

GitHubリポジトリにエミュレータによって得られた盤面データと、生成され得る $65536$ 通りの盤面を書き出すプログラムを公開しています。

左右にも上下にもドロップ種類についても対称性がないとは驚きです。
某ゲームのように秒単位の時刻をシードにしたりはしていないので乱数調整はできなさそうで残念
乱数とそれによる盤面の重複はさすがに改善されていると思いますが、それ以外は現行のスマホ版パズドラに残っていてもおかしくない仕様です。
特にドロップの種類ごとの出現率の偏りは場合によっては攻略に影響してくるかもしれません。

記事には書いていない試行錯誤が多数あります。大変でした、ぽ

正確には、そのようにドロップが揃って消えるのが $2$ 回以上起こることをコンボと呼びますが、この記事ではドロップが $3$ つ揃っていること自体をコンボと呼ぶことにします。 ↩