1. はじめに
画像の前処理の技術力向上のためにこちらを実践 画像処理100本ノック!!
とっかかりやすいようにColaboratoryでやります。
目標は２週間で完了できるようにやっていきます。丁寧に解説します。質問バシバシください！
001 - 010 は右のリンク 画像処理100本ノック!!(001 - 010)丁寧にじっくりと
011 - 020 は右のリンク 画像処理100本ノック!!(011 - 020)序盤戦
021 - 030 は右のリンク 画像処理100本ノック!!(021 - 030)一息入れたい・・・
2. 前準備
ライブラリ等々を以下のように導入。
# ライブラリをインポート
from google.colab import drive
import numpy as np
import matplotlib.pyplot as plt
import cv2
from google.colab.patches import cv2_imshow
# 画像の読み込み
img = cv2.imread('画像のパス/imori.jpg')
img_noise = cv2.imread('画像のパス/imori_noise.jpg')
img_dark = cv2.imread('画像のパス/imori_dark.jpg')
img_gamma = cv2.imread('画像のパス/imori_gamma.jpg')
# グレースケール画像
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
gray_noise = cv2.cvtColor(img_noise, cv2.COLOR_BGR2GRAY)
gray_dark = cv2.cvtColor(img_dark, cv2.COLOR_BGR2GRAY)
# 画像保存用
OUT_DIR = '出力先のパス/OUTPUT/'
3.解説
Q.31. アフィン変換(スキュー)
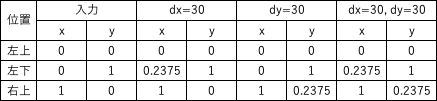
1)アフィン変換を用いて、出力(1)のようなX-sharing(dx = 30)画像を作成せよ。
(2)アフィン変換を用いて、出力2のようなY-sharing(dy = 30)画像を作成せよ。
(3)アフィン変換を用いて、出力3のような幾何変換した(dx = 30, dy = 30)画像を作成せよ。
このような画像はスキュー画像と呼ばれ、画像を斜め方向に伸ばした画像である。
出力(1)の場合、x方向にdxだけ引き伸ばした画像はX-sharingと呼ばれる。
出力(2)の場合、y方向にdyだけ引き伸ばした画像はY-sharingと呼ばれる。
それぞれ次式のアフィン変換で実現できる。 ただし、元画像のサイズがh x wとする。
A31
def affine_skew(img, dx, dy):
"""
params
------------------------------
param1: numpy.ndarray形式のimage
param2: x軸方向のスキュー
param2: y軸方向のスキュー
returns
------------------------------
numpy.ndarray形式のimage
"""
# 画像の高さ、幅、色を取得
H, W = img.shape[:2]
# xy座標をnp.float32型(3点分のxy座標)
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = src.copy()
# 変換後の3点の座標
dest[:,0] += (dx / W * (src[:,1])).astype(np.float32)
dest[:,1] += (dy / H * (src[:,0])).astype(np.float32)
"""
アフィン変換の変換行列を生成: cv2.getAffineTransform(src, dest)
src: 変換前の3点の座標
dest: 変換後の3点の座標をNumPy配列ndarrayで指定
"""
affine = cv2.getAffineTransform(src, dest)
"""
アフィン変換
cv2.warpAffine(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]])
第一引数に元画像（NumPy配列ndarray）、
第二引数に2 x 3の変換行列（NumPy配列ndarray）、
第三引数に出力画像のサイズ（タプル）を指定する。
"""
return cv2.warpAffine(img, affine, (W+dx, H+dy))
# X-sharing(dx = 30)画像
out1 = affine_skew(img, 30, 0)
# Y-sharing(dy = 30)画像
out2 = affine_skew(img, 0, 30)
# 幾何変換した(dx = 30, dy = 30)画像
out3 = affine_skew(img, 30, 30)
# 結果を保存する
cv2.imwrite(OUT_DIR + 'ans31_1.jpg', out1)
cv2.imwrite(OUT_DIR + 'ans31_2.jpg', out2)
cv2.imwrite(OUT_DIR + 'ans31_3.jpg', out3)
# 画像を表示
cv2_imshow(out1)
cv2_imshow(out2)
cv2_imshow(out3)
cv2.waitKey(0)
cv2.destroyAllWindows()
座標の変換イメージは下記参照
参考: 完全に理解するアフィン変換
Q.32. フーリエ変換
二次元離散フーリエ変換(DFT)を実装し、imori.jpgをグレースケール化したものの周波数のパワースペクトルを表示せよ。 また、逆二次元離散フーリエ変換(IDFT)で画像を復元せよ。
二次元離散フーリエ変換(DFT: Discrete Fourier Transformation)とはフーリエ変換の画像に対する処理方法である。
通常のフーリエ変換はアナログ信号や音声などの連続値かつ一次元を対象に周波数成分を求める計算処理である。
一方、ディジタル画像は[0,255]の離散値をとり、かつ画像はHxWの二次元表示であるので、二次元離散フーリエ変換が行われる。
二次元離散フーリエ変換(DFT)は次式で計算される。
K = [0, W-1], l = [0, H-1], 入力画像を I として
ここでは画像をグレースケール化してから二次元離散フーリエ変換を行え。
パワースペクトルとは Gは複素数で表されるので、Gの絶対値を求めることである。 今回のみ画像表示の時はパワースペクトルは[0,255]にスケーリングせよ。
逆二次元離散フーリエ変換(IDFT: Inverse DFT)とは周波数成分Gから元の画像を復元する手法であり、次式で定義される。
x = [0, W-1], y = [0, H-1] として
上が定義式ですがexp(j)は複素数の値をとってしまうので、実際にコードにするときはぜ下式のように絶対値を使います
シンプルに全部for文で回すと128^4の計算になるので、時間がかかってしまいます。numpyをうまく活用すれば計算コストを減らすことができます。（解答は128^2まで減らしました。）
A32
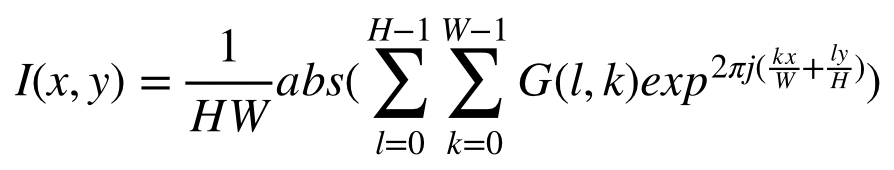
# 2次元離散フーリエ変換 (DFT)のハイパーパラメーター
K, L = 128, 128
channel = 3
def dft(img):
"""
2次元離散フーリエ変換 (DFT)
params
--------------------------------------
param: numpy.ndarray形式のimage
returns
------------------------------
周波数成分G
"""
# 画像の高さ、幅を取得
H, W = img.shape[:2]
# DFT係数(np.complex: 複素数を扱うための型)
G = np.zeros((L, K, channel), dtype=np.complex)
# 元のイメージと一致(NumPy配列ndarrayをタイル状に繰り返し並べるnp.tile)
x = np.tile(np.arange(W), (H, 1)) # >>> [0 1 2 ・・・・ 125 126 127]
y = np.arange(H).repeat(W).reshape(H, -1) # >>> [0 0 0 0]・・・・[127 127 127・・・]
# DFTの計算(周波数成分G)
for c in range(channel):
for l in range(L):
for k in range(K):
G[l, k, c] = np.sum(img[..., c] * np.exp(-2j * np.pi * (x * k / K + y * l / L))) / np.sqrt(K * L)
return G
# IDFT(逆二次元離散フーリエ変換)
def idft(G):
"""
逆二次元離散フーリエ変換 (IDFT)
params
--------------------------------------
param: 周波数成分G
returns
------------------------------
numpy.ndarray形式のimage
"""
# 画像の高さ、幅を取得
H, W = G.shape[:2]
# DFT係数(np.complex: 複素数を扱うための型)
out = np.zeros((H, W, channel), dtype=np.float32)
# 元のイメージと一致(NumPy配列ndarrayをタイル状に繰り返し並べるnp.tile)
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# IDFT(逆二次元離散フーリエ変換)
for c in range(channel):
for l in range(H):
for k in range(W):
out[l, k, c] = np.abs(np.sum(G[..., c] * np.exp(2j * np.pi * (x * k / W + y * l / H)))) / np.sqrt(W * H)
# clipping(NumPy配列ndarrayを任意の最小値・最大値に収めるclip)
# 0 ~ 255の範囲
out = np.clip(out, 0, 255)
out = out.astype(np.uint8)
return out
# 2次元離散フーリエ変換
G = dft(img)
# 周波数のパワースペクトル
ps = (np.abs(G) / np.abs(G).max() * 255).astype(np.uint8)
cv2.imwrite("out_ps.jpg", ps)
# 逆二次元離散フーリエ変換
out = idft(G)
# 保存
cv2_imshow(out)
cv2.waitKey(0)
cv2.imwrite("img32.jpg", out)
OpenCVがカラーでできないのが残念
参考: 【Python/OpenCV】高速フーリエ変換でパワースペクトルの算出
参考: フーリエ変換
Q.33. フーリエ変換 ローパスフィルタ
imori.jpgをグレースケール化したものをDFTし、ローパスフィルタを通してIDFTで画像を復元せよ。
DFTによって得られた周波数成分は左上、右上、左下、右下に近いほど低周波数の成分を含んでいることになり、中心に近いほど高周波成分を示す。
画像における高周波成分とは色が変わっている部分（ノイズや輪郭など）を示し、低周波成分とは色があまり変わっていない部分（夕日のグラデーションなど）を表す。 ここでは、高周波成分をカットし、低周波成分のみを通すローパスフィルタを実装せよ。ここでは低周波数の中心から高周波までの距離をrとすると0.5rまでの成分を通すとする。
A33
# 2次元離散フーリエ変換 (DFT)のハイパーパラメーター
K, L = 128, 128
channel = 3
def dft(img):
"""
2次元離散フーリエ変換 (DFT)
params
--------------------------------------
param: numpy.ndarray形式のimage
returns
------------------------------
周波数成分G
"""
# 画像の高さ、幅を取得
H, W = img.shape[:2]
# DFT係数(np.complex: 複素数を扱うための型)
G = np.zeros((L, K, channel), dtype=np.complex)
# 元のイメージと一致(NumPy配列ndarrayをタイル状に繰り返し並べるnp.tile)
x = np.tile(np.arange(W), (H, 1)) # >>> [0 1 2 ・・・・ 125 126 127]
y = np.arange(H).repeat(W).reshape(H, -1) # >>> [0 0 0 0]・・・・[127 127 127・・・]
# DFTの計算(周波数成分G)
for c in range(channel):
for l in range(L):
for k in range(K):
G[l, k, c] = np.sum(img[..., c] * np.exp(-2j * np.pi * (x * k / K + y * l / L))) / np.sqrt(K * L)
return G
# IDFT(逆二次元離散フーリエ変換)
def idft(G):
"""
逆二次元離散フーリエ変換 (IDFT)
params
--------------------------------------
param: 周波数成分G
returns
------------------------------
numpy.ndarray形式のimage
"""
# 画像の高さ、幅を取得
H, W = G.shape[:2]
# DFT係数(np.complex: 複素数を扱うための型)
out = np.zeros((H, W, channel), dtype=np.float32)
# 元のイメージと一致(NumPy配列ndarrayをタイル状に繰り返し並べるnp.tile)
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# IDFT(逆二次元離散フーリエ変換)
for c in range(channel):
for l in range(H):
for k in range(W):
out[l, k, c] = np.abs(np.sum(G[..., c] * np.exp(2j * np.pi * (x * k / W + y * l / H)))) / np.sqrt(W * H)
# clipping(NumPy配列ndarrayを任意の最小値・最大値に収めるclip)
# 0 ~ 255の範囲
out = np.clip(out, 0, 255)
out = out.astype(np.uint8)
return out
def lpf(G, ratio=0.5):
"""
ローパスフィルタ: 信号の低周波数成分のみを通過
params
--------------------------------------
param1: 周波数成分G
param2: 割合
returns
------------------------------
周波数成分G
"""
# 画像の高さ、幅を取得
H, W = G.shape[:2]
# 元の配列と同じ形状の配列を生成
_G = np.zeros_like(G)
# 第1象限と第3象限、第1象限と第4象限を入れ替え
_G[:H//2, :W//2] = G[H//2:, W//2:]
_G[:H//2, W//2:] = G[H//2:, :W//2]
_G[H//2:, :W//2] = G[:H//2, W//2:]
_G[H//2:, W//2:] = G[:H//2, :W//2]
# fsrc = np.fft.fftshift(src)
# 元のイメージと一致(NumPy配列ndarrayをタイル状に繰り返し並べるnp.tile)
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# フィルターの作成
_x = x - W // 2
_y = y - H // 2
r = np.sqrt(_x ** 2 + _y ** 2)
# マスクの作成
mask = np.ones((H, W), dtype=np.float32)
mask[r > (W // 2 * ratio)] = 0
mask = np.repeat(mask, channel).reshape(H, W, channel)
# フィルタリング
_G *= mask
# 入れ替え
G[:H//2, :W//2] = _G[H//2:, W//2:]
G[:H//2, W//2:] = _G[H//2:, :W//2]
G[H//2:, :W//2] = _G[:H//2, W//2:]
G[H//2:, W//2:] = _G[:H//2, :W//2]
return G
H, W, C = img.shape
# 2次元離散フーリエ変換
G = dft(img)
# ローパスフィルタ
G = lpf(G)
# 逆二次元離散フーリエ変換
out = idft(G)
# 保存
cv2_imshow(out)
cv2.waitKey(0)
cv2.imwrite("img33.jpg", out)
参考: 【Python/OpenCV】フーリエ変換+ローパスフィルタでノイズ除去
##Q.34. フーリエ変換 ハイパスフィルタ
imori.jpgをグレースケール化したものをDFTし、ハイパスフィルタを通してIDFTで画像を復元せよ。
ここでは、低周波成分をカットし、高周波成分のみを通すハイパスフィルタを実装せよ。
ここでは低周波数の中心から高周波までの距離をrとすると0.1rからの成分を通すとする。
A34
# 2次元離散フーリエ変換 (DFT)のハイパーパラメーター
K, L = 128, 128
channel = 3
def dft(img):
"""
2次元離散フーリエ変換 (DFT)
params
--------------------------------------
param: numpy.ndarray形式のimage
returns
------------------------------
周波数成分G
"""
# 画像の高さ、幅を取得
H, W = img.shape[:2]
# DFT係数(np.complex: 複素数を扱うための型)
G = np.zeros((L, K, channel), dtype=np.complex)
# 元のイメージと一致(NumPy配列ndarrayをタイル状に繰り返し並べるnp.tile)
x = np.tile(np.arange(W), (H, 1)) # >>> [0 1 2 ・・・・ 125 126 127]
y = np.arange(H).repeat(W).reshape(H, -1) # >>> [0 0 0 0]・・・・[127 127 127・・・]
# DFTの計算(周波数成分G)
for c in range(channel):
for l in range(L):
for k in range(K):
G[l, k, c] = np.sum(img[..., c] * np.exp(-2j * np.pi * (x * k / K + y * l / L))) / np.sqrt(K * L)
return G
# IDFT(逆二次元離散フーリエ変換)
def idft(G):
"""
逆二次元離散フーリエ変換 (IDFT)
params
--------------------------------------
param: 周波数成分G
returns
------------------------------
numpy.ndarray形式のimage
"""
# 画像の高さ、幅を取得
H, W = G.shape[:2]
# DFT係数(np.complex: 複素数を扱うための型)
out = np.zeros((H, W, channel), dtype=np.float32)
# 元のイメージと一致(NumPy配列ndarrayをタイル状に繰り返し並べるnp.tile)
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# IDFT(逆二次元離散フーリエ変換)
for c in range(channel):
for l in range(H):
for k in range(W):
out[l, k, c] = np.abs(np.sum(G[..., c] * np.exp(2j * np.pi * (x * k / W + y * l / H)))) / np.sqrt(W * H)
# clipping(NumPy配列ndarrayを任意の最小値・最大値に収めるclip)
# 0 ~ 255の範囲
out = np.clip(out, 0, 255)
out = out.astype(np.uint8)
return out
def hpf(G, ratio=0.1):
"""
ハイパスフィルタは、信号の高周波数成分のみを通過させる。
params
--------------------------------------
param: 周波数成分G
returns
------------------------------
周波数成分G
"""
H, W = G.shape[:2]
# 第1象限と第3象限、第1象限と第4象限を入れ替え
_G = np.zeros_like(G)
_G[:H//2, :W//2] = G[H//2:, W//2:]
_G[:H//2, W//2:] = G[H//2:, :W//2]
_G[H//2:, :W//2] = G[:H//2, W//2:]
_G[H//2:, W//2:] = G[:H//2, :W//2]
# 中心からの距離
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# フィルター作成
_x = x - W // 2
_y = y - H // 2
r = np.sqrt(_x ** 2 + _y ** 2)
# マスクの作成
mask = np.ones((H, W), dtype=np.float32)
mask[r < (W // 2 * ratio)] = 0
mask = np.repeat(mask, channel).reshape(H, W, channel)
# フィルタリング
_G *= mask
# 入れ替え
G[:H//2, :W//2] = _G[H//2:, W//2:]
G[:H//2, W//2:] = _G[H//2:, :W//2]
G[H//2:, :W//2] = _G[:H//2, W//2:]
G[H//2:, W//2:] = _G[:H//2, :W//2]
return G
# DFT
G = dft(img)
# HPF
G = hpf(G)
# IDFT
out = idft(G)
# 画像表示
cv2_imshow(out)
cv2.waitKey(0)
cv2.imwrite("img34.jpg", out)
OpenCVでやろうとしたがうまくいかず、実行もかなり遅い。要改善。
##Q.35. フーリエ変換 バンドパスフィルタ
imori.jpgをグレースケール化したものをDFTし、ハイパスフィルタを通してIDFTで画像を復元せよ。
ここでは、低周波成分と高周波成分の中間の周波数成分のみを通すハイパスフィルタを実装せよ。
ここでは低周波数の中心から高周波までの距離をrとすると0.1rから0.5rまでの成分を通すとする。
A35
# 2次元離散フーリエ変換 (DFT)のハイパーパラメーター
K, L = 128, 128
channel = 3
def dft(img):
"""
2次元離散フーリエ変換 (DFT)
params
--------------------------------------
param: numpy.ndarray形式のimage
returns
------------------------------
周波数成分G
"""
# 画像の高さ、幅を取得
H, W = img.shape[:2]
# DFT係数(np.complex: 複素数を扱うための型)
G = np.zeros((L, K, channel), dtype=np.complex)
# 元のイメージと一致(NumPy配列ndarrayをタイル状に繰り返し並べるnp.tile)
x = np.tile(np.arange(W), (H, 1)) # >>> [0 1 2 ・・・・ 125 126 127]
y = np.arange(H).repeat(W).reshape(H, -1) # >>> [0 0 0 0]・・・・[127 127 127・・・]
# DFTの計算(周波数成分G)
for c in range(channel):
for l in range(L):
for k in range(K):
G[l, k, c] = np.sum(img[..., c] * np.exp(-2j * np.pi * (x * k / K + y * l / L))) / np.sqrt(K * L)
return G
# IDFT(逆二次元離散フーリエ変換)
def idft(G):
"""
逆二次元離散フーリエ変換 (IDFT)
params
--------------------------------------
param: 周波数成分G
returns
------------------------------
numpy.ndarray形式のimage
"""
# 画像の高さ、幅を取得
H, W = G.shape[:2]
# DFT係数(np.complex: 複素数を扱うための型)
out = np.zeros((H, W, channel), dtype=np.float32)
# 元のイメージと一致(NumPy配列ndarrayをタイル状に繰り返し並べるnp.tile)
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# IDFT(逆二次元離散フーリエ変換)
for c in range(channel):
for l in range(H):
for k in range(W):
out[l, k, c] = np.abs(np.sum(G[..., c] * np.exp(2j * np.pi * (x * k / W + y * l / H)))) / np.sqrt(W * H)
# clipping(NumPy配列ndarrayを任意の最小値・最大値に収めるclip)
# 0 ~ 255の範囲
out = np.clip(out, 0, 255)
out = out.astype(np.uint8)
return out
def bpf(G, ratio1=0.1, ratio2=0.5):
"""
バンドパスフィルタ: ある帯域のみを通したいときに使います
params
--------------------------------------
param1: 周波数成分G
param2: 成分範囲
param3: 成分範囲
returns
------------------------------
周波数成分G
"""
H, W, _ = G.shape
# 第1象限と第3象限、第1象限と第4象限を入れ替え
_G = np.zeros_like(G)
_G[:H//2, :W//2] = G[H//2:, W//2:]
_G[:H//2, W//2:] = G[H//2:, :W//2]
_G[H//2:, :W//2] = G[:H//2, W//2:]
_G[H//2:, W//2:] = G[:H//2, :W//2]
# 中心からの距離
x = np.tile(np.arange(W), (H, 1))
y = np.arange(H).repeat(W).reshape(H, -1)
# フィルター作成
_x = x - W // 2
_y = y - H // 2
r = np.sqrt(_x ** 2 + _y ** 2)
# マスクの作成
mask = np.ones((H, W), dtype=np.float32)
# 範囲を指定
mask[(r < (W // 2 * ratio1)) | (r > (W // 2 * ratio2))] = 0
mask = np.repeat(mask, channel).reshape(H, W, channel)
# フィルタリング
_G *= mask
# 入れ替え
G[:H//2, :W//2] = _G[H//2:, W//2:]
G[:H//2, W//2:] = _G[H//2:, :W//2]
G[H//2:, :W//2] = _G[:H//2, W//2:]
G[H//2:, W//2:] = _G[:H//2, :W//2]
return G
# DFT
G = dft(img)
# BPF
G = bpf(G)
# IDFT
out = idft(G)
# 画像表示
cv2_imshow(out)
cv2.waitKey(0)
cv2.imwrite("img35.jpg", out)
参考: 画像処理におけるフーリエ変換④〜pythonによるフィルタ設計〜
Q.36. JPEG圧縮 (Step.1)離散コサイン変換
imori.jpgをグレースケール化し離散コサイン変換を行い、逆離散コサイン変換を行え。
離散コサイン変換(DCT: Discrete Cosine Transformation)とは、次式で定義される周波数変換の一つである。
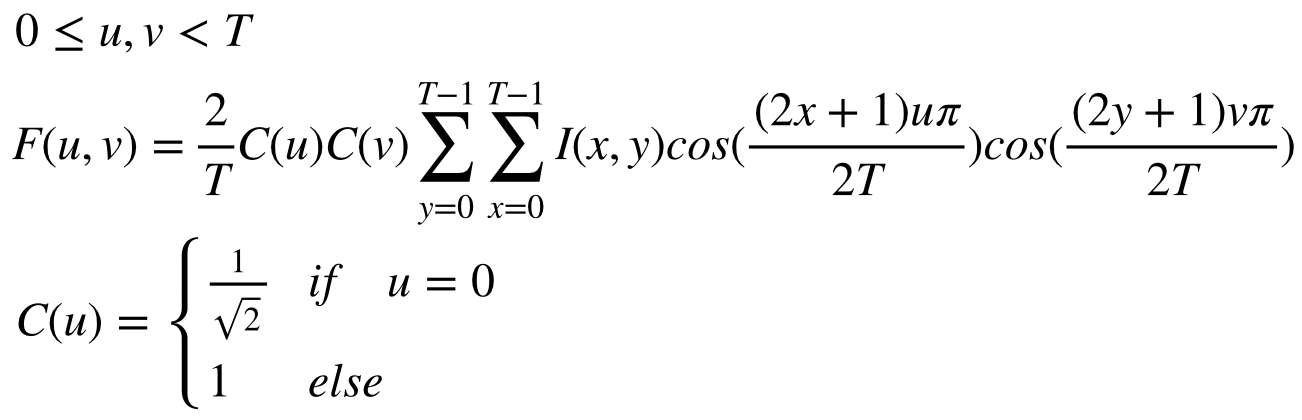逆離散コサイン変換(IDCT: Inverse Discrete Cosine Transformation)とは離散コサイン変換の逆（復号）であり、次式で定義される。 ここでいう K は復元時にどれだけ解像度を良くするかを決定するパラメータである。 K = Tの時は、DCT係数を全部使うのでIDCT後の解像度は最大になるが、Kが１や２などの時は復元に使う情報量（DCT係数）が減るので解像度が下がる。これを適度に設定することで、画像の容量を減らすことができる。
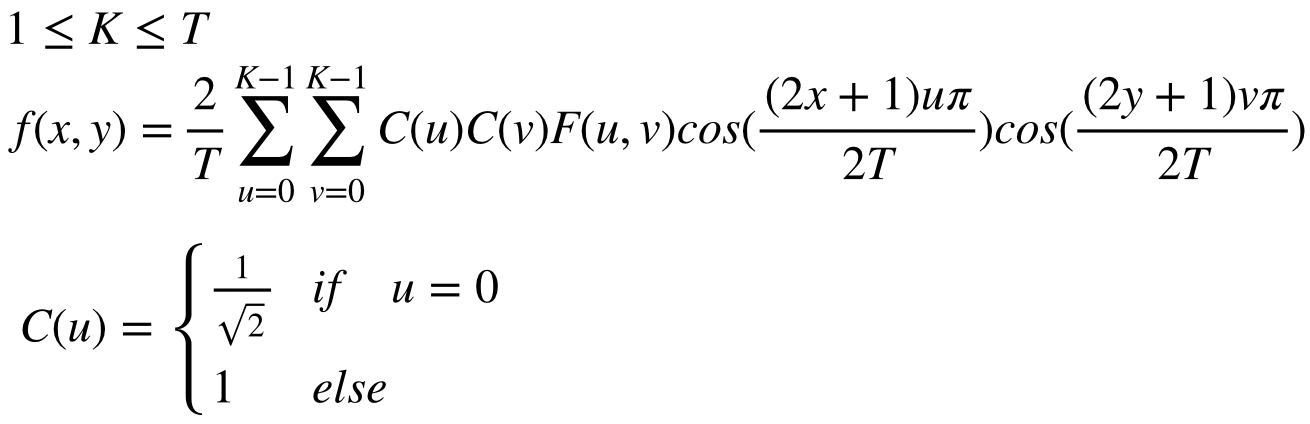ここでは画像を8x8ずつの領域に分割して、各領域で以上のDCT, IDCTを繰り返すことで、jpeg符号に応用される。 今回も同様に8x8の領域に分割して、DCT, IDCTを行え。
A36
# DCT hyoer-parameter
T = 8
K = 8 # 復元時にどれだけ解像度を良くするかを決定するパラメータ
channel = 3
# DCT weight
def w(x, y, u, v):
"""
離散コサイン変換(DCT: Discrete Cosine Transformation) の係数
params
-------------------------------
returns
-------------------------------
係数
"""
cu = 1.
cv = 1.
if u == 0:
cu /= np.sqrt(2)
if v == 0:
cv /= np.sqrt(2)
theta = np.pi / (2 * T)
return (( 2 * cu * cv / T) * np.cos((2*x+1)*u*theta) * np.cos((2*y+1)*v*theta))
# DCT
def dct(img):
"""
離散コサイン変換(DCT: Discrete Cosine Transformation)
params
-----------------------------
img: numpy.ndarray形式のimage
returns
-----------------------------
離散コサイン変換(DCT: Discrete Cosine Transformation)
"""
# 画像の高さ、幅を取得
H, W, _ = img.shape
# 0を要素とする配列を生成する
F = np.zeros((H, W, channel), dtype=np.float32)
# rgbそれぞれのチャネル
for c in range(channel):
# 縦方向にT(8)の間隔
for yi in range(0, H, T):
# 横方向にT(8)の間隔
for xi in range(0, W, T):
for v in range(T):
for u in range(T):
for y in range(T):
for x in range(T):
# 各画素に対して離散コサイン変換
F[v+yi, u+xi, c] += img[y+yi, x+xi, c] * w(x,y,u,v)
return F
# IDCT
def idct(F):
"""
逆離散コサイン変換
params
-----------------------------
F： 離散コサイン変換
returns
-----------------------------
逆離散コサイン変換
"""
# 画像の高さ、幅を取得
H, W, _ = F.shape
# 0を要素とする配列を生成する
out = np.zeros((H, W, channel), dtype=np.float32)
for c in range(channel):
for yi in range(0, H, T):
for xi in range(0, W, T):
for y in range(T):
for x in range(T):
for v in range(K):
for u in range(K):
out[y+yi, x+xi, c] += F[v+yi, u+xi, c] * w(x,y,u,v)
# clipping(NumPy配列ndarrayを任意の最小値・最大値に収めるclip)
out = np.clip(out, 0, 255)
out = np.round(out).astype(np.uint8)
return out
# DCT
F = dct(img)
# IDCT
out = idct(F)
# 画像表示
cv2_imshow(out)
cv2.waitKey(0)
cv2.imwrite("img36.jpg", out)
参考: 「離散コサイン変換」４－７【４章 三角関数、数学大百科事典】
こちらに関しては説明が難しい・・・
##Q.37. PSNR
IDCTで用いるDCT係数を8でなく、4にすると画像の劣化が生じる。 入力画像とIDCT画像のPSNRを求めよ。また、IDCTによるビットレートを求めよ。
**PSNR(Peak Signal to Noise Ratio)**とは信号対雑音比と呼ばれ、画像がどれだけ劣化したかを示す。
PSNRが大きいほど、画像が劣化していないことを示し、次式で定義される。 v_maxは取りうる値の最大値で[0,255]の表示なら v_max=255 となる。
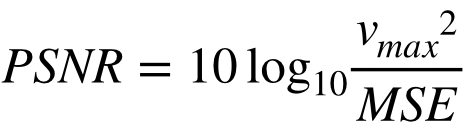式中のMSEは**Mean Squared Error(平均二乗誤差)**と呼ばれ、二つの画像の差分の二乗の平均値を示す。
ビットレートとは8x8でDCTを行い、IDCTでKxKの係数までを用いた時に次式で定義される。
A37
# DCT hyoer-parameter
T = 8
K = 4
channel = 3
# DCT weight
def w(x, y, u, v):
"""
離散コサイン変換(DCT: Discrete Cosine Transformation) の係数
params
-------------------------------
returns
-------------------------------
係数
"""
cu = 1.
cv = 1.
if u == 0:
cu /= np.sqrt(2)
if v == 0:
cv /= np.sqrt(2)
theta = np.pi / (2 * T)
return (( 2 * cu * cv / T) * np.cos((2*x+1)*u*theta) * np.cos((2*y+1)*v*theta))
# DCT
def dct(img):
"""
離散コサイン変換(DCT: Discrete Cosine Transformation)
params
-----------------------------
img: numpy.ndarray形式のimage
returns
-----------------------------
離散コサイン変換(DCT: Discrete Cosine Transformation)
"""
# 画像の高さ、幅を取得
H, W, _ = img.shape
# 0を要素とする配列を生成する
F = np.zeros((H, W, channel), dtype=np.float32)
# rgbそれぞれのチャネル
for c in range(channel):
# 縦方向にT(8)の間隔
for yi in range(0, H, T):
# 横方向にT(8)の間隔
for xi in range(0, W, T):
for v in range(T):
for u in range(T):
for y in range(T):
for x in range(T):
# 各画素に対して離散コサイン変換
F[v+yi, u+xi, c] += img[y+yi, x+xi, c] * w(x,y,u,v)
return F
# IDCT
def idct(F):
"""
逆離散コサイン変換
params
-----------------------------
F： 離散コサイン変換
returns
-----------------------------
逆離散コサイン変換
"""
# 画像の高さ、幅を取得
H, W, _ = F.shape
# 0を要素とする配列を生成する
out = np.zeros((H, W, channel), dtype=np.float32)
for c in range(channel):
for yi in range(0, H, T):
for xi in range(0, W, T):
for y in range(T):
for x in range(T):
for v in range(K):
for u in range(K):
out[y+yi, x+xi, c] += F[v+yi, u+xi, c] * w(x,y,u,v)
# clipping(NumPy配列ndarrayを任意の最小値・最大値に収めるclip)
out = np.clip(out, 0, 255)
out = np.round(out).astype(np.uint8)
return out
# MSE
def MSE(img1, img2):
"""
平均二乗誤差
params
-----------------------------
img1: numpy.ndarray形式のimage
img2: numpy.ndarray形式のimage
returns
-----------------------------
平均二乗誤差の値 class 'numpy.float64'
"""
# 画像の高さ、幅を取得
H, W, _ = img1.shape
# 二つの画像の差分の二乗
mse = np.sum((img1 - img2) ** 2) / (H * W * channel) # 47.437601725260414
return mse
# PSNR
def PSNR(mse, vmax=255):
"""
信号対雑音比: イメージ間のピーク S/N 比 (PSNR) の計算
params
------------------------------
mse: 平均二乗誤差の値
vmax: 値の最大値で[0,255]
returns
------------------------------
信号対雑音比 class 'numpy.float64'
"""
return 10 * np.log10(vmax * vmax / mse) # 31.369576363256535
# bitrate
def BITRATE():
"""
ビットレート class 'float'
"""
return 1. * T * K * K / T / T #2.0
# DCT
F = dct(img)
# IDCT
out = idct(F)
# MSE
mse = MSE(img, out)
# PSNR
psnr = PSNR(mse)
# bitrate
bitrate = BITRATE()
print("MSE:", type(mse))
print("PSNR:", type(psnr))
print("bitrate:", type(bitrate))
# 画像表示
cv2_imshow(out)
cv2.waitKey(0)
cv2.imwrite("img37.jpg", out)
参考: MathWorks
##Q.38. JPEG圧縮 (Step.2)DCT+量子化
DCT係数を量子化し、IDCTで復元せよ。また、その時の画像の容量を比べよ。
DCT係数を量子化することはjpeg画像にする符号化で用いられる手法である。
量子化とは、値を予め決定された区分毎に値を大まかに丸め込む作業であり、floorやceil, roundなどが似た計算である。
JPEG画像ではDCT係数を下記で表される量子化テーブルに則って量子化する。 この量子化テーブルはjpeg団体の仕様書から取った。 量子化では8x8の係数をQで割り、四捨五入する。その後Qを掛けることで行われる。 IDCTでは係数は全て用いるものとする。
Q = np.array(((16, 11, 10, 16, 24, 40, 51, 61),
(12, 12, 14, 19, 26, 58, 60, 55),
(14, 13, 16, 24, 40, 57, 69, 56),
(14, 17, 22, 29, 51, 87, 80, 62),
(18, 22, 37, 56, 68, 109, 103, 77),
(24, 35, 55, 64, 81, 104, 113, 92),
(49, 64, 78, 87, 103, 121, 120, 101),
(72, 92, 95, 98, 112, 100, 103, 99)), dtype=np.float32)
量子化を行うと画像の容量が減っていることから、データ量が削減されたことが伺える。
A38
# DCT hyoer-parameter
T = 8
K = 4
channel = 3
# DCT weight
def w(x, y, u, v):
"""
離散コサイン変換(DCT: Discrete Cosine Transformation) の係数
params
-------------------------------
returns
-------------------------------
係数
"""
cu = 1.
cv = 1.
if u == 0:
cu /= np.sqrt(2)
if v == 0:
cv /= np.sqrt(2)
theta = np.pi / (2 * T)
return (( 2 * cu * cv / T) * np.cos((2*x+1)*u*theta) * np.cos((2*y+1)*v*theta))
# DCT
def dct(img):
"""
離散コサイン変換(DCT: Discrete Cosine Transformation)
params
-----------------------------
img: numpy.ndarray形式のimage
returns
-----------------------------
離散コサイン変換(DCT: Discrete Cosine Transformation)
"""
# 画像の高さ、幅を取得
H, W, _ = img.shape
# 0を要素とする配列を生成する
F = np.zeros((H, W, channel), dtype=np.float32)
# rgbそれぞれのチャネル
for c in range(channel):
# 縦方向にT(8)の間隔
for yi in range(0, H, T):
# 横方向にT(8)の間隔
for xi in range(0, W, T):
for v in range(T):
for u in range(T):
for y in range(T):
for x in range(T):
# 各画素に対して離散コサイン変換
F[v+yi, u+xi, c] += img[y+yi, x+xi, c] * w(x,y,u,v)
return F
# IDCT
def idct(F):
"""
逆離散コサイン変換
params
-----------------------------
F： 離散コサイン変換
returns
-----------------------------
逆離散コサイン変換
"""
# 画像の高さ、幅を取得
H, W, _ = F.shape
# 0を要素とする配列を生成する
out = np.zeros((H, W, channel), dtype=np.float32)
for c in range(channel):
for yi in range(0, H, T):
for xi in range(0, W, T):
for y in range(T):
for x in range(T):
for v in range(K):
for u in range(K):
out[y+yi, x+xi, c] += F[v+yi, u+xi, c] * w(x,y,u,v)
# clipping(NumPy配列ndarrayを任意の最小値・最大値に収めるclip)
out = np.clip(out, 0, 255)
out = np.round(out).astype(np.uint8)
return out
def quantization(F):
"""
DCT係数を量子化
params
-------------------------------
F: DCT係数
returns
-------------------------------
DCT係数を量子化
"""
# 画像の高さ、幅を取得
H, W, _ = F.shape
# 量子化では8x8の係数をQで割り、四捨五入
Q = np.array(((16, 11, 10, 16, 24, 40, 51, 61),
(12, 12, 14, 19, 26, 58, 60, 55),
(14, 13, 16, 24, 40, 57, 69, 56),
(14, 17, 22, 29, 51, 87, 80, 62),
(18, 22, 37, 56, 68, 109, 103, 77),
(24, 35, 55, 64, 81, 104, 113, 92),
(49, 64, 78, 87, 103, 121, 120, 101),
(72, 92, 95, 98, 112, 100, 103, 99)), dtype=np.float32)
for ys in range(0, H, T):
for xs in range(0, W, T):
for c in range(channel):
F[ys: ys + T, xs: xs + T, c] = np.round(F[ys: ys + T, xs: xs + T, c] / Q) * Q
return F
def MSE(img1, img2):
"""
平均二乗誤差
params
-----------------------------
img1: numpy.ndarray形式のimage
img2: numpy.ndarray形式のimage
returns
-----------------------------
平均二乗誤差の値 class 'numpy.float64'
"""
# 画像の高さ、幅を取得
H, W, _ = img1.shape
# 二つの画像の差分の二乗
mse = np.sum((img1 - img2) ** 2) / (H * W * channel)
return mse
# PSNR
def PSNR(mse, vmax=255):
"""
信号対雑音比: イメージ間のピーク S/N 比 (PSNR) の計算
params
------------------------------
mse: 平均二乗誤差の値
vmax: 値の最大値で[0,255]
returns
------------------------------
信号対雑音比 class 'numpy.float64'
"""
return 10 * np.log10(vmax * vmax / mse)
def BITRATE():
"""
ビットレート class 'float'
"""
return 1. * T * K * K / T / T
# DCT
F = dct(img)
# quantization
F = quantization(F)
# IDCT
out = idct(F)
# MSE
mse = MSE(img, out)
# PSNR
psnr = PSNR(mse)
# bitrate
bitrate = BITRATE()
print("MSE:", mse)
print("PSNR:", psnr)
print("bitrate:", bitrate)
# 画像表示
cv2_imshow(out)
cv2.waitKey(0)
cv2.imwrite("img38.jpg", out)
参考: 量子化行列のナゾ～その１
##Q.39. JPEG圧縮 (Step.3)YCbCr表色系
YCbCr表色形において、Yを0.7倍してコントラストを暗くせよ。
YCbCr表色系とは、画像を明るさを表すY、輝度と青レベルの差Cb、輝度と赤レベルの差Crに分解する表現方法である。
これはJPEG変換で用いられる。
A39
def y_change(img, y):
"""
brg => YCrCbへ変換し、コントラストを変える
YCrCb => bgrへ変換
params
---------------------------------
img: numpy.ndarray形式のimage
y: yのコントラストの数値(倍数)
returns
---------------------------------
numpy.ndarray形式のimage
"""
# rgb => YCrCbへ変換
YCrCb = cv2.cvtColor(img, cv2.COLOR_BGR2YCR_CB)
# Yを0.7倍
YCrCb[..., 0] = YCrCb[..., 0] * 0.7
# YCrCb => bgrへ変換
out = cv2.cvtColor(YCrCb, cv2.COLOR_YCrCb2BGR)
return out
# YCbCr表色系
out = y_change(img, 0.7)
# 保存
cv2_imshow(out)
cv2.waitKey(0)
cv2.imwrite("img39.jpg", out)
参考: Python OpenCV：YCbCrをRGBに戻す方法は？
##Q.40. JPEG圧縮 (Step.4)YCbCr+DCT+量子化
YCbCr表色系にし、DCT後、Yを量子化テーブルQ1、CbとCrをQ2で量子化し、IDCTで画像を復元せよ。 また、画像の容量を比較せよ。
アルゴリズムは、
- RGB を YCbCrに変換
- YCbCrをDCT
- DCTしたものを量子化
- 量子化したものをIDCT
- IDCTしたYCbCrをRGBに変換
これはJPEGで実際に使われるデータ量削減の手法であり、Q1,Q2はJPEGの仕様書に則って次式で定義される。
A40
def BGR2YCbCr(img):
"""
bgr => YCrCbへ変換
params
---------------------------------
img: numpy.ndarray形式のimage
returns
---------------------------------
numpy.ndarray形式のimage
"""
# rgb => YCrCbへ変換
YCrCb = cv2.cvtColor(img, cv2.COLOR_BGR2YCR_CB)
return YCrCb
def YCbCr2BGR(img):
"""
YCbCr => bgrへ変換
params
---------------------------------
img: numpy.ndarray形式のimage
returns
---------------------------------
numpy.ndarray形式のimage
"""
# YCbCr => bgへ変換
bgr = cv2.cvtColor(YCrCb, cv2.COLOR_YCrCb2BGR)
return bgr
# DCT hyoer-parameter
T = 8
K = 4
channel = 3
# DCT weight
def w(x, y, u, v):
"""
離散コサイン変換(DCT: Discrete Cosine Transformation) の係数
params
-------------------------------
returns
-------------------------------
係数
"""
cu = 1.
cv = 1.
if u == 0:
cu /= np.sqrt(2)
if v == 0:
cv /= np.sqrt(2)
theta = np.pi / (2 * T)
return (( 2 * cu * cv / T) * np.cos((2*x+1)*u*theta) * np.cos((2*y+1)*v*theta))
# DCT
def dct(img):
"""
離散コサイン変換(DCT: Discrete Cosine Transformation)
params
-----------------------------
img: numpy.ndarray形式のimage
returns
-----------------------------
離散コサイン変換(DCT: Discrete Cosine Transformation)
"""
# 画像の高さ、幅を取得
H, W, _ = img.shape
# 0を要素とする配列を生成する
F = np.zeros((H, W, channel), dtype=np.float32)
# rgbそれぞれのチャネル
for c in range(channel):
# 縦方向にT(8)の間隔
for yi in range(0, H, T):
# 横方向にT(8)の間隔
for xi in range(0, W, T):
for v in range(T):
for u in range(T):
for y in range(T):
for x in range(T):
# 各画素に対して離散コサイン変換
F[v+yi, u+xi, c] += img[y+yi, x+xi, c] * w(x,y,u,v)
return F
# IDCT
def idct(F):
"""
逆離散コサイン変換
params
-----------------------------
F： 離散コサイン変換
returns
-----------------------------
逆離散コサイン変換
"""
# 画像の高さ、幅を取得
H, W, _ = F.shape
# 0を要素とする配列を生成する
out = np.zeros((H, W, channel), dtype=np.float32)
for c in range(channel):
for yi in range(0, H, T):
for xi in range(0, W, T):
for y in range(T):
for x in range(T):
for v in range(K):
for u in range(K):
out[y+yi, x+xi, c] += F[v+yi, u+xi, c] * w(x,y,u,v)
# clipping(NumPy配列ndarrayを任意の最小値・最大値に収めるclip)
out = np.clip(out, 0, 255)
out = np.round(out).astype(np.uint8)
return out
def quantization(F):
"""
DCT係数を量子化
params
-------------------------------
F: DCT係数
returns
-------------------------------
DCT係数を量子化
"""
# 画像の高さ、幅を取得
H, W, _ = F.shape
# 量子化では8x8の係数をQで割り、四捨五入
Q = np.array(((16, 11, 10, 16, 24, 40, 51, 61),
(12, 12, 14, 19, 26, 58, 60, 55),
(14, 13, 16, 24, 40, 57, 69, 56),
(14, 17, 22, 29, 51, 87, 80, 62),
(18, 22, 37, 56, 68, 109, 103, 77),
(24, 35, 55, 64, 81, 104, 113, 92),
(49, 64, 78, 87, 103, 121, 120, 101),
(72, 92, 95, 98, 112, 100, 103, 99)), dtype=np.float32)
for ys in range(0, H, T):
for xs in range(0, W, T):
for c in range(channel):
F[ys: ys + T, xs: xs + T, c] = np.round(F[ys: ys + T, xs: xs + T, c] / Q) * Q
return F
def JPEG(img):
"""
jpeg圧縮
params
------------------------------------
img: numpy.ndarray形式のimage
returns
------------------------------------
numpy.ndarray形式のimage
"""
# BGR -> YCbCr
YCbCr = BGR2YCbCr(img)
# DCT
F = dct(YCbCr)
# DCT係数を量子化
F = quantization(F)
# IDCT
YCbCr = idct(F)
# Y Cb Cr -> BGR
out = YCbCr2BGR(YCbCr)
return out
def MSE(img1, img2):
"""
平均二乗誤差
params
-----------------------------
img1: numpy.ndarray形式のimage
img2: numpy.ndarray形式のimage
returns
-----------------------------
平均二乗誤差の値 class 'numpy.float64'
"""
# 画像の高さ、幅を取得
H, W, _ = img1.shape
# 二つの画像の差分の二乗
mse = np.sum((img1 - img2) ** 2) / (H * W * channel)
return mse
# PSNR
def PSNR(mse, vmax=255):
"""
信号対雑音比: イメージ間のピーク S/N 比 (PSNR) の計算
params
------------------------------
mse: 平均二乗誤差の値
vmax: 値の最大値で[0,255]
returns
------------------------------
信号対雑音比 class 'numpy.float64'
"""
return 10 * np.log10(vmax * vmax / mse)
def BITRATE():
"""
ビットレート class 'float'
"""
return 1. * T * K * K / T / T
# JPEG
out = JPEG(img)
# MSE
mse = MSE(img, out)
# PSNR
psnr = PSNR(mse)
# bitrate
bitrate = BITRATE()
print("MSE:", mse)
print("PSNR:", psnr)
print("bitrate:", bitrate)
# 画像表示
cv2_imshow(out)
cv2.waitKey(0)
cv2.imwrite("img40.jpg", out)
感想
内容が賀くんと難しくなった。うまく説明できていない部分は随時更新していく