優先順位付きキューを理解してみた

はじめに

新年の目標として毎日leetcodeのdaily challengeを解くようにしていますが、今日の問題は以下のものでした。

🤔🤔🤔🤔🤔

水たまりにどれだけ水が溜まっているかを計算するということだけはわかりました。

まず1時間をかけて格闘してみたのですが、解けず...

諦めてsolutionを見るとMin heap(最小ヒープ)、優先順位キュー、完全２分木などのワードが出てきていました。バイナリーツリーについて概念は知っているけど...

ということで今回は優先順位付きキューについて理解してみました！

Heap（ヒープ）とは？

Web開発をしているとブラウザのヒープメモリを使う、みたいな言葉はよく聞いていたのですが、そもそもヒープとはなんでしょう？

定義

英語での言葉の意味だけで見ると、「集合体」のような意味合いを持ちます。

そして、コンピューターサイエンス的には以下のような意味です。

ヒープ（heap）とは、データ構造の一種で、木構造(ツリー構造)のうち、親要素が子要素より常に大きい(あるいは小さい)という条件を満たすもの。また、コンピュータプログラムが利用するメモリ領域の種類の一つで、実行時に任意のタイミングで確保や解放が可能なものをヒープ領域というが、これをヒープと略す場合がある。

優先度がつけられている

要するに、ヒープは優先順位がある大きな箱です。

救急病院だと、患者が来た時緊急度をもとに診療を行う必要があります。
先着順ではなく緊急度を考える必要がありますよね。

このような時にヒープを使うことができます。

種類

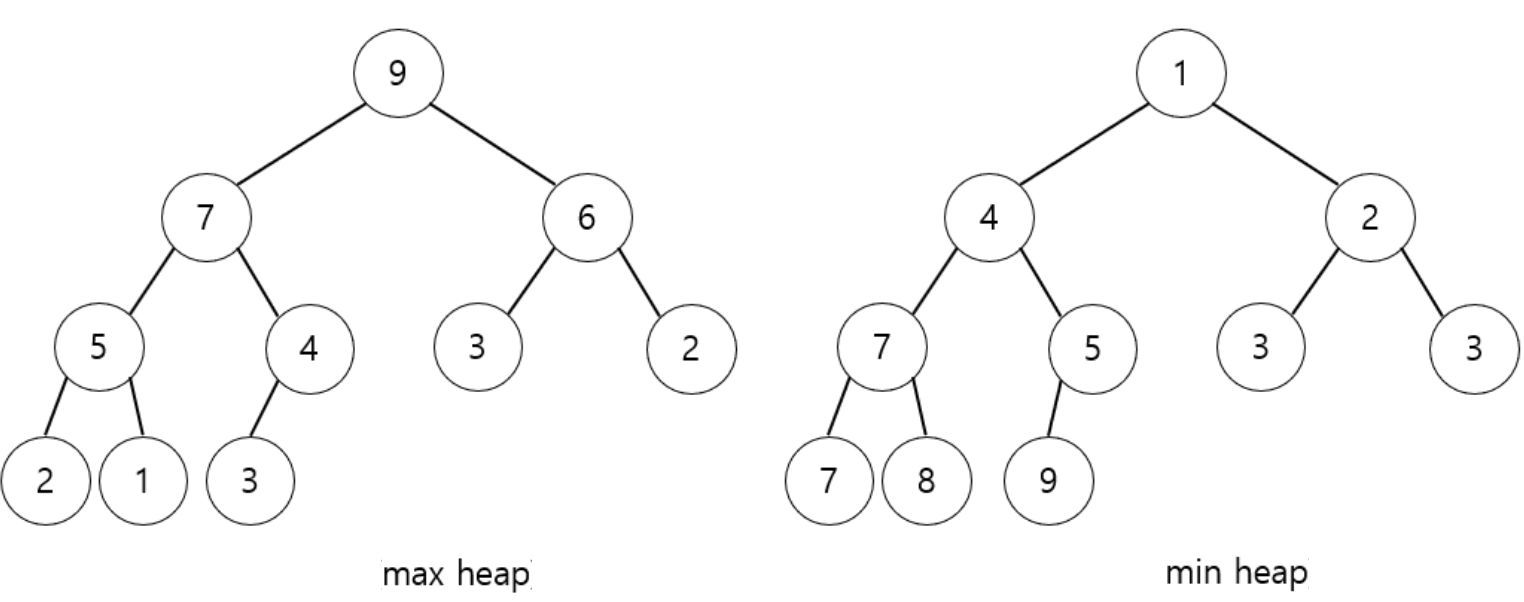
このヒープは大きな数字から並べるとMax Heap（最大ヒープ）、小さい数字から並べるとMin Heapで分けられます。

以下図のようなイメージです。

特性

1. 親は子より小さい（Min Heap)か大きい（Max Heap）
2. 必ず左から埋める必要がある（空きを許さない）

このような特性を持つ構造を完全２分木と呼びます。

上の図を見るとわかるように、２分探索木と違って重複があってもいいです。

概念の整理

ヒープ、優先順位付き、完全２分木という言葉が出てきて少しわかりにくくなりましたね。
ここで一旦概念を整理したいと思います。

完全二分木

以下のような形だけを表す概念です

• 最下層を除いて、全ての層がノードで埋まっている
• 最下層は左から順に詰めて配置される

これは「構造」を説明する用語です。

ヒープ

完全二分木の形を持ちながら、親子間の大小関係が決まっているデータ構造

データ構造のことです。

優先度付きキュー

優先度の高い要素から順に取り出せるもの全てを指す言葉です。
その実装方法の1つとしてヒープがよく使われるって感じです。

抽象的な「データの型」を意味します。

Insert

ヒープを使うと何が嬉しいかを知るために、ヒープの挿入演算について考えていきたいと思います。

引き続き救急病院のケースで、以下のようなヒープを考えてみましょう。
勝手に症状に優先度をつけてみています。

　1(心臓麻痺)
   /   \
3(骨折) 4(風邪)

ここで、2(急性アレルギー反応)という新しい患者が入ってきたとします。
そうすると以下のようなロジックで患者を処理して行きます。

1. とりあえずヒープの最後に入れる

　　　1
   /   \
  4     3
 /
2

1. 親と比較する
   2は4より小さい？　→ 「はい」であるため2と4の位置を交換します。

     1
   /   \
  2     3
 /
4

1. 続けて親と比較
   2は1より小さい？　→ 「いいえ」であるため、処理を止める

そうやって新しい値は

1. 最も深い層の左に詰めて入れて
2. 親より小さかったら上に登って
3. 親より大きかったら止まる

処理を続けることによって正しい優先順位の位置を探して入ります。

おわりに

やはりデータ構造やアルゴリズム自体を知らないとどう頑張っても解けない問題がありますよね...

思考の範囲を広げるためにももっと勉強していきたいですね！

出典