この記事では木構造に関するアルゴリズム**「HL 分解 (Heavy-Light Decomposition,HLD とも)」について紹介します.このアルゴリズムを理解すると,様々な「木のパスに対するクエリ」**に対応できるようになります.
HL 分解は少し難易度が高いですが,この記事では図を使って視覚的に理解できます.是非 HL 分解をものにしてください!
1. HL 分解とは
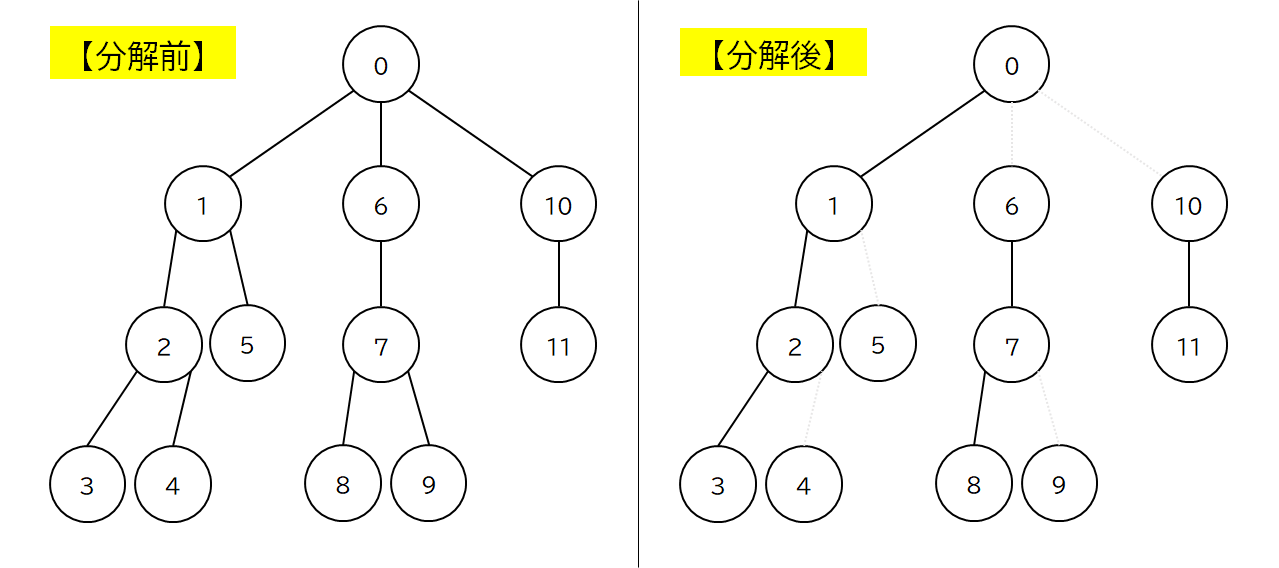
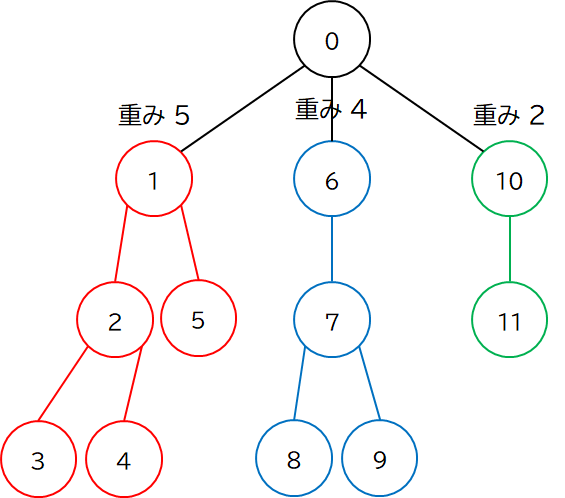
HL 分解では 根つき木 をバラバラに分解していきます (普通の木を根つき木にしながら HL 分解することもできます).
まずは分解後どうなるのか見てみましょう.
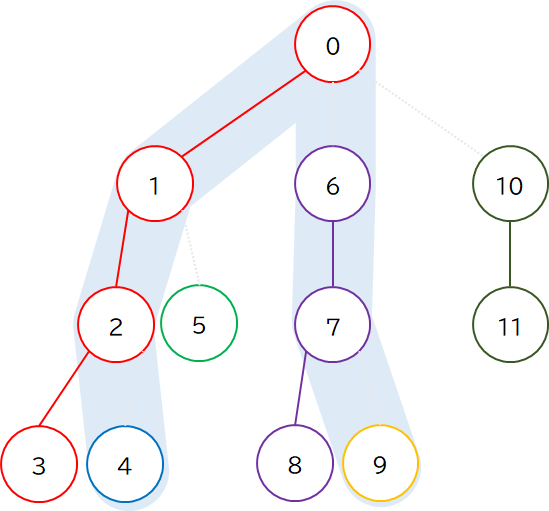
上図のうち,灰色点線になっている辺が,分解されて切られた辺です.
Heavy な頂点だけつなぐ
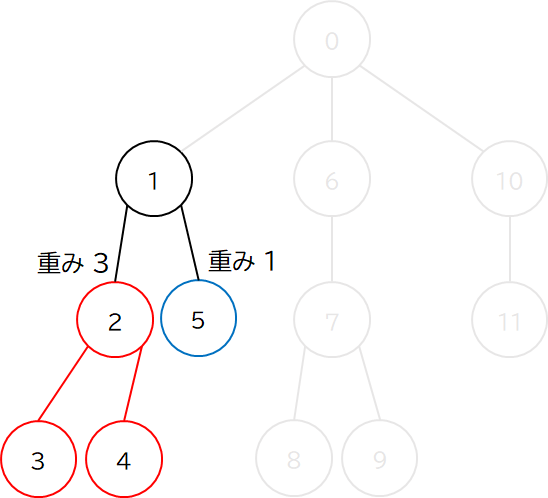
Heavy-Light 分解というからには,各頂点 (または辺) の**「重み」**が重要になってきます.ここでは,各頂点について「重み」を その頂点を根とする部分木の要素数 と定義します.部分木の要素数が多ければ多いほど,Heavy な頂点ということになります.
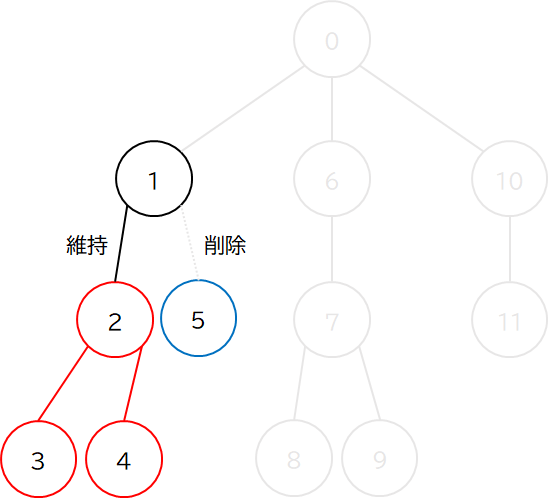
そして,ある頂点について,その子供たちのうち,最も重みが大きい頂点 (Heavy な頂点) との辺だけを維持します.それ以外の頂点 (Light な頂点) との辺は切ってしまいます.
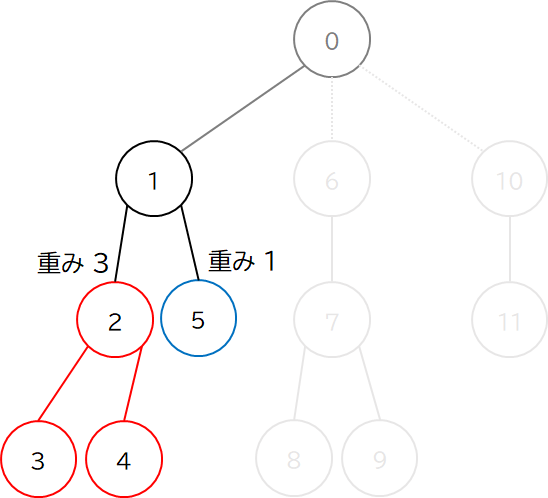
例えば上図の頂点 1 の場合,子は 2 個あって,頂点 2 は重み 3,頂点 5 は重み 1 です,よって,頂点 2 は Heavy な頂点なので頂点 2 との辺は維持し,頂点 5 は Light な頂点なので頂点 5 との辺は切ってしまいます.
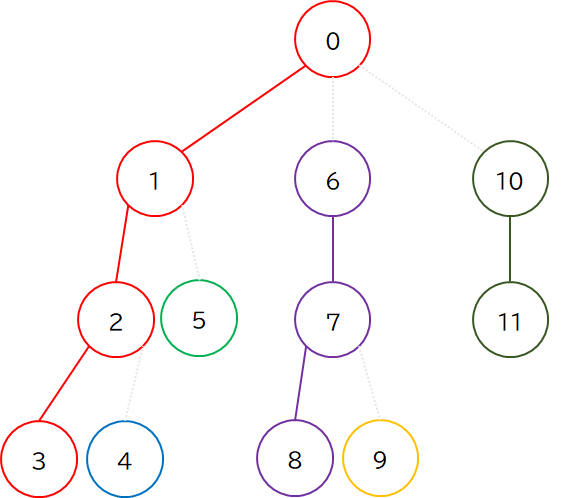
この分解をすべての頂点について行うと,次のような結果が得られます.このとき,どの色の連結成分も 枝分かれが無い直線状 になっているのがポイントです.(ある頂点から出ている辺は多くても,親への辺と子のうち 1 個との辺の 2 辺しかなく,つまりどの頂点も次数 2 以下であることから示されます.)
2. HL 分解の実装方針
なぜ HL 分解がパスクエリに強いのか気になるかもしれませんが,先に具体的な実装方法を見ていきます.
HL 分解は根から 再帰的に 行うと実装が楽です.まずは根 (図の頂点 0) について,子供たちの重みを比べます.
この場合,頂点 1 が一番重い (Heavy) なので,頂点 1 との辺だけ維持して,他の辺はすべて切ってしまいます.
次に Heavy な頂点に推移して,再帰的に HL 分解をします.
今度は頂点 2 が Heavy なので,頂点 2 との辺だけ維持して,頂点 5 との辺を切ってしまいます.
これを繰り返すと,図のような分解結果が得られます.(各頂点に振られた番号は,再帰関数でたどる順番になっています.)
辺を繋いだままにする子は 1 つだけで,それ以外はすべて切ってしまうので,実際は HL 結合と言えるかもしれません.Heavy な頂点だけ結合していきます.
これで,HL 分解は完了です!
なお,各部分木の大きさ,つまり重みを求めるときに,毎回再帰関数を回すと毎回 $O(N)$ かかるので,メモ化しましょう.
分解結果をデータ構造に割り当てる
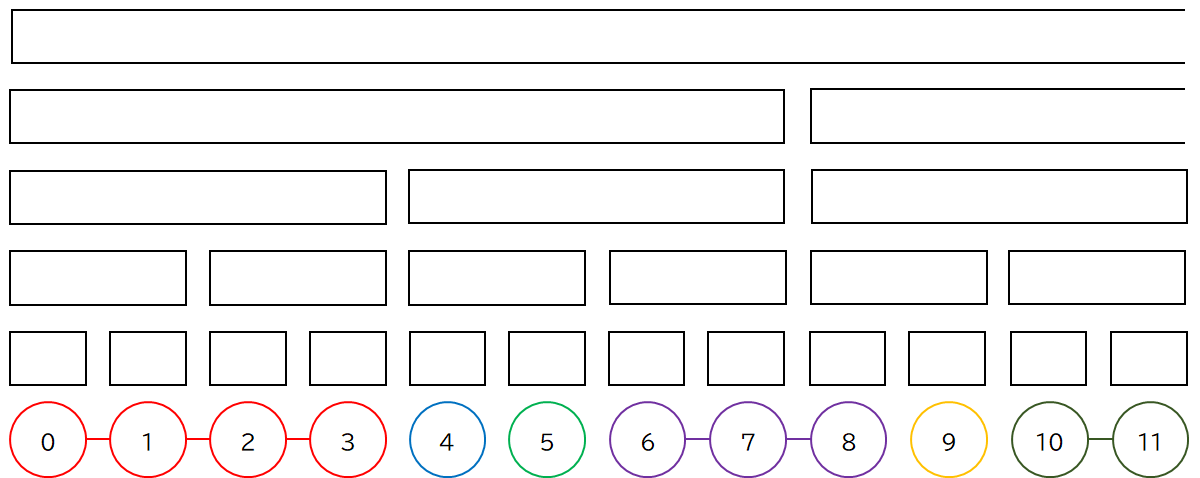
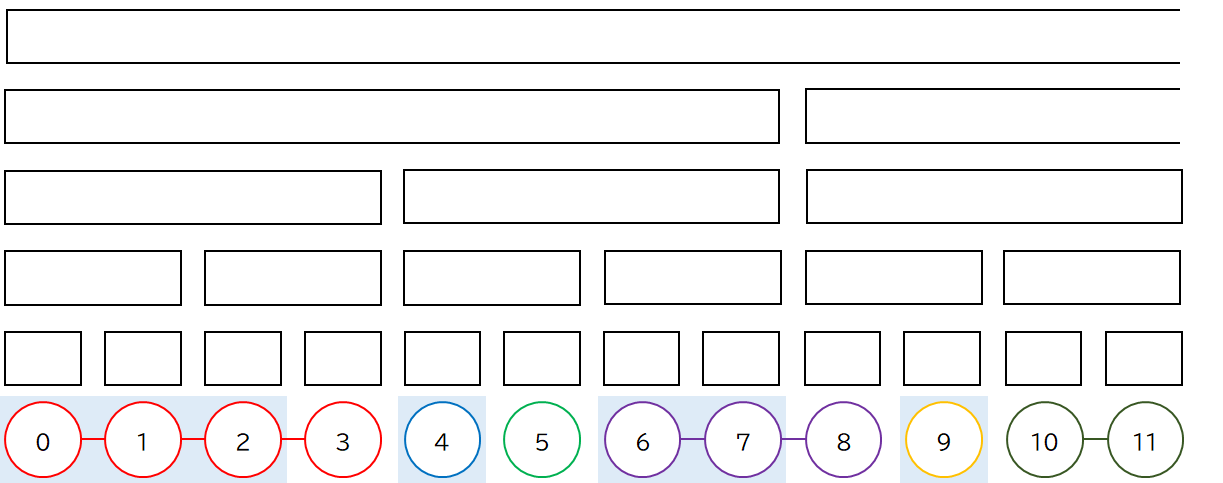
この分解結果を 1 直線に並べなおしてみます.再帰的に分解をしながらたどる際に,初めて訪問したときの順番を可変長配列 vector などで管理しておくと,訪問順がそのまま並べなおした結果になるので便利です.
そして,必要に応じてこの結果をデータ構造に割り当てます.例えば Segment Tree の場合,次のようになります.
なぜ訪問順をデータ構造に割り当てるのか
上で訪問順をもとに各ノードを 1 直線にならべて,データ構造に割り当てると書きましたが,これは HL 分解の結果の使い方の話であり,必須ではありません.
このように,連結成分の数だけデータ構造を用意しても大丈夫です.
しかし,1 直線に並べることで実装が比較的簡単になり,しかもこの実装方法であれば列は行きがけ順になっているので,部分木に対するクエリにも対応しやすいです.なので,この記事では HL 分解後,訪問順で 1 列に並べることにします.
Twitter でアンケートを行ってみても,1 列に並べている方が多かったです.
3. なぜ HL 分解はパスクエリに強いのか?
冒頭に紹介したように,HL 分解を行うと,木のパス (経路) に対する様々なクエリに対応できるようになります.これはなぜでしょうか?
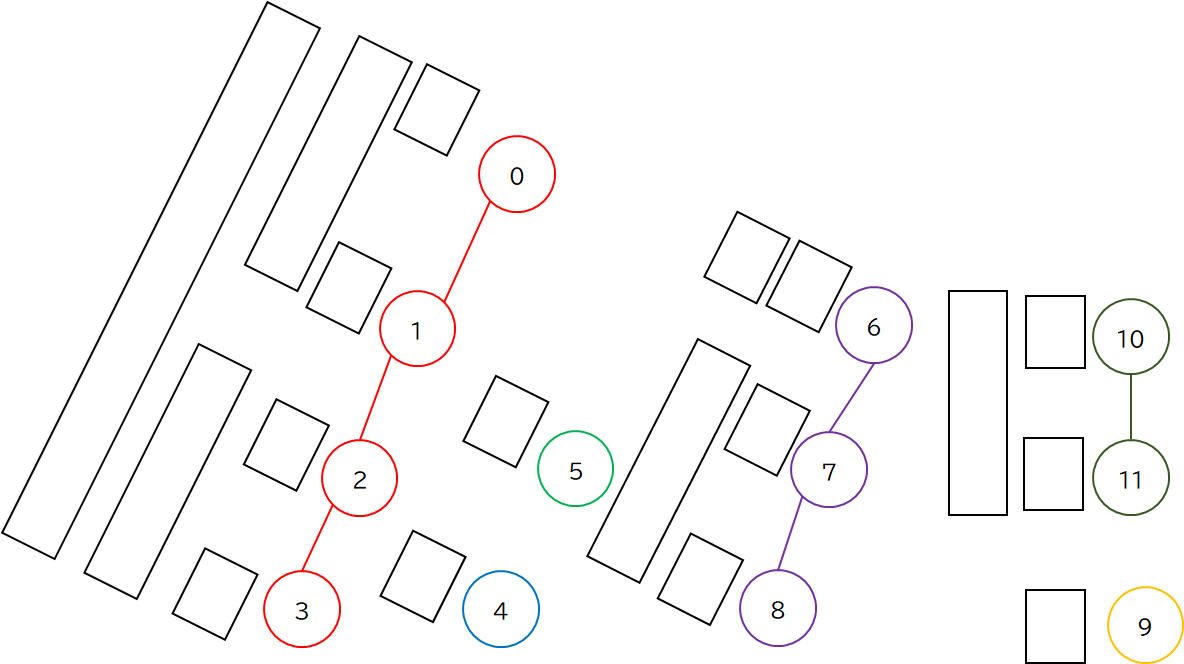
実は,木上の任意のパスについて,通る連結成分は $O(\log N)$ 個であることが証明できます.
例えば上図の頂点 4 から頂点 9 までのパスの場合,通る連結成分は青・赤・紫・黄の 4 個です.
証明は後にして,この性質がどんなことに使えるのか考えてみます.
例題:木上の Range Minimum Query
各頂点に値が割り振られた頂点数 $N$ の木が与えられるので,次の 2 種類のクエリを処理してください.
- 頂点 $v$ の値を $x$ に変更する
- 頂点 $v$ から頂点 $u$ まで最短経路で移動したときに通る頂点の値の最小値を求める (両端含む)
もしこの問題が木についてではなく,数列についてであればどうでしょうか?
この場合は典型的な Range Minimum Query の問題になり,Segment Tree を利用して,クエリ当たり $O(\log N)$ で処理できます.
よって,任意のパスが通る連結成分は $O(\log N)$ 個なので,各連結成分ごとに Segment Tree を使用した処理を行えば,木の場合も $O(\log^2 N)$ で各クエリを処理することができます.
通る連結成分が $O(\log N)$ 個であるということは,Range Minimum Query で処理しないといけない区間が $O(\log N)$ 個ということです.$O(\log N)$ 個の区間それぞれで $O(\log N)$ の処理をするので,全体では $O(\log^2 N)$ でクエリを処理できるということになります.
なぜどんなパスも O(log N) 個の連結成分を通るのか?
厳密な証明は他の方にお任せするとして,ここでは直感的な説明を考えます.
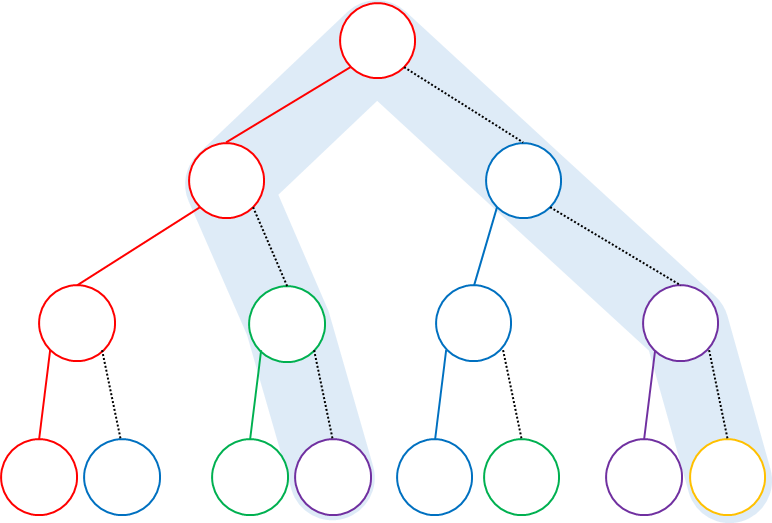
最も多く連結成分を通るパス,つまり最悪ケースについて考えてみましょう.
木を構築しながらこのようなパスを考えます.
まずは根です.
- 頂点数が多ければ多いほど,パスは多くの連結成分を通ることができるので,根を通らないのは損です.根は通りましょう.
- 根の子についてですが,パスは高々 2 つの子しか通ることができないので,子が 3 個以上になると損です.また,子が 1 個だと連結成分の数が増えないので損です.よって,根の子は 2 個にしましょう.この 2 個の子はどちらも通ります.
- 根の子の要素数の配分ですが,いくらでもいいのですが,便宜上半々にしておきます.
次に根以外の通ることが確定している頂点について再帰的に考えます.
- パスのうち片方の端は親の方から伸びてきているので,子のうち通れるのは 1 個だけです.
- 根の場合と同様,子は 2 個にするのがお得です.
- なるべく多くの連結成分を通りたいわけなので,Light な方の子にパスを伸ばします.
- 子の要素数の配分ですが,パスが伸びた Light な方の子になるべくたくさん要素をあげるとお得なので,半々にします.
これを繰り返しながら最悪ケースの木を構築すると,平衡二分木 になります.平衡二分木の高さは $O(\log N)$ です.
よって,どんなパスも通る頂点数が $O(\log N)$ 個になるので,通る連結成分の数も $O(\log N)$ 個です.
ちなみに,根の子の要素数の配分は便宜上半々にしましたが,極端な例として $N-2 : 1$ に配分した場合,次のようになります.
この場合も結局,ほぼ平衡二分木になっていて,通る連結成分の個数にオーダーレベルの差異はありません.
4. 実装例
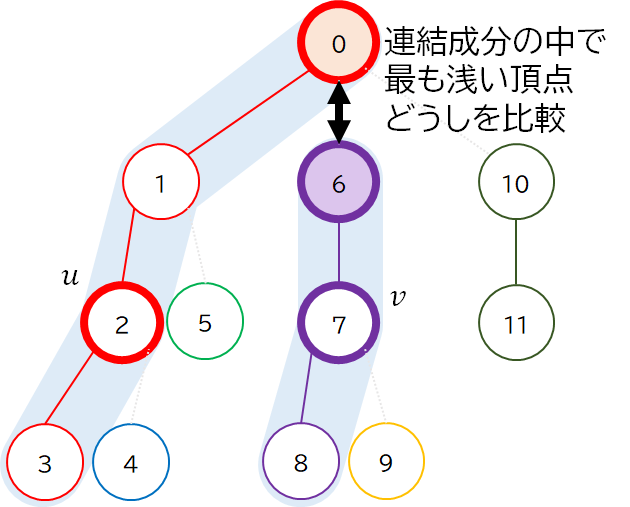
実装の説明では触れませんでしたが,各連結成分ごとに最も浅い頂点をメモしておきます.あるパスに対応する区間を求めるには,連結成分のうち最も浅い頂点が深い方から登っていけばいいです.このとき,その最も浅い頂点の親に飛びます.
では実装例です.入力が 0-indexed で次のように与えられると仮定しています.
$N$
$p_0$ $p_1$ $\cdots$ $p_{N-1}$
$Q$
$u_0$ $v_0$
$u_1$ $v_1$
$\vdots$
$u_{Q-1}$ $v_{Q-1}$
$p_i$ は頂点 $i$ の親で,$-1$ の場合はその頂点が根です.
各クエリは「頂点 $u_i$ と 頂点 $v_i$ を結ぶパスを表す $O(\log N)$ 個の区間」を出力します.
# include<bits/stdc++.h>
using namespace std;
# define MAX_N 100000
int N;
int p[MAX_N]; // 親
vector<int> c[MAX_N]; // 子のリスト
int Q;
int s[MAX_N] = {};
// 頂点 v を根とする部分木の要素数を求める
int siz(int v){
if(s[v] != 0) return s[v];
s[v] = 1;
for(int i=0; i<c[v].size(); i++) s[v] += siz(c[v][i]);
return s[v];
}
vector<int> hld;
int pre[MAX_N];
int A[MAX_N]; // 連結成分のうち最も浅い頂点
// HL 分解を行う
void HLD(int v, int a){
pre[v] = hld.size();
hld.push_back(v);
A[v] = a;
if(c[v].size() == 0) return;
int M = 0;
int idx = -1;
for(int i=0; i<c[v].size(); i++){
if(siz(c[v][i]) > M){
M = siz(c[v][i]);
idx = i;
}
}
HLD(c[v][idx], a);
for(int i=0; i<c[v].size(); i++){
if(i != idx) HLD(c[v][i], c[v][i]);
}
}
int d[MAX_N] = {};
// 頂点 v の深さを求める
int depth(int v){
if(d[v] != 0) return d[v];
if(p[v] == -1) return 0;
return d[v] = 1+depth(p[v]);
}
// クエリを処理する
vector<pair<int,int>> query(int u, int v){
vector<pair<int,int>> ret;
while(A[u] != A[v]){
if(depth(A[u]) <= depth(A[v])){
ret.push_back({pre[A[v]], pre[v]});
v = p[A[v]];
}
else{
ret.push_back({pre[A[u]], pre[u]});
u = p[A[u]];
}
}
ret.push_back({min(pre[u],pre[v]), max(pre[u], pre[v])});
return ret;
}
int main(){
cin >> N;
for(int i=0; i<N; i++){
cin >> p[i];
c[p[i]].push_back(i);
}
for(int i=0; i<N; i++){
if(p[i] == -1) HLD(i, i);
}
cin >> Q;
for(int i=0; i<Q; i++){
int u, v;
cin >> u >> v;
vector<pair<int,int>> ans = query(u, v);
for(int j=0; j<ans.size(); j++){
cout << "[" << ans[j].first << ", " << ans[j].second << "] ";
}
cout << endl;
}
}
※ 未 verify です.
入力例
12
-1 0 1 2 2 1 0 6 7 7 0 10
1
4 9
出力結果
[9, 9] [4, 4] [6, 7] [0, 2]
ちなみに,最後の区間の first の方が頂点 $u$,$v$ の LCA (Lowest Common Ancestor,最小共通祖先) になっています.
5. HL 分解のまとめ
- 部分木の要素数が多い Heavy な頂点との辺だけを残す処理を再帰的に繰り返します
- 直線上の複数の連結成分に分かれます
- 各頂点を列に関するデータ構造と対応させます
- どんなパスについても,通る連結成分は $O(\log N)$ 個です
- パスと対応する区間を登りながら求めます
以上により,例えば Segment Tree ( $O(\log N)$ ) と対応させればクエリ当たり $O(\log^2 N)$ で処理できるし,区間加算して最後に各頂点の値を求めるような問題なら imos 法 ( $O(1)$ ) が使えてクエリ当たり $O(\log N)$ で処理できます.
これで,木のパスに関するクエリを列に対するクエリに読み替えることができました.パスクエリは怖くない!
最後までお読みいただきありがとうございました.是非 LGTM をお願いします! 励みになります.
6. HL 分解を使う問題たち
ネタバレ防止のため,畳んでいます.
他にも見つけ次第追加します.