【図解】線形時間の文字列アルゴリズム「Z algorithm」をイラストとアニメーションでかみ砕く

この記事では文字列を $S$，その $i$ $(0 \leq i < |S|)$ 文字目を $S[i]$ と表記します．文字列の結合は $+$ で表現します．
また，Z 配列を $Z$，その $i$ $(0 \leq i < |S|)$ 番目の要素を $Z[i]$ と表記します．

1. Z algorithm で求める Z 配列とは

難しく厳密に表現すると，$Z[i]$ は

• 文字列 $S=S[0]+S[1]+\cdots+S[|S|-1]$
• 文字列 $S[i]+S[i+1]+\cdots+S[|S|-1]$
  の 最長共通接頭辞の長さ と定義されます．

もう少しざっくり表現すると，

• 文字列 $S=S[0]+S[1]+\cdots+S[|S|-1]$
• 文字列 $S[i]+S[i+1]+\cdots+S[|S|-1]$
  の 先頭何文字が一致してるの？ という値が $Z[i]$ です．

図解

図でも確認します．次の文字列**「モモもスモモも酢」**を考えてみます．

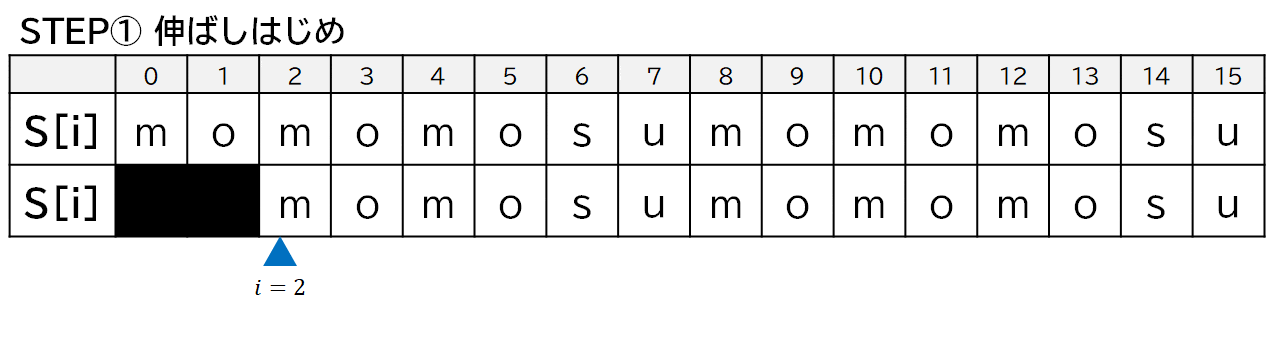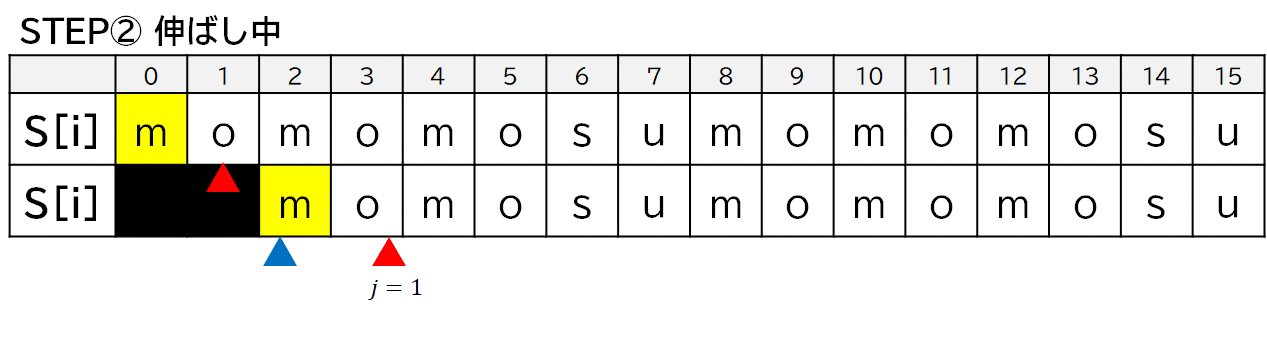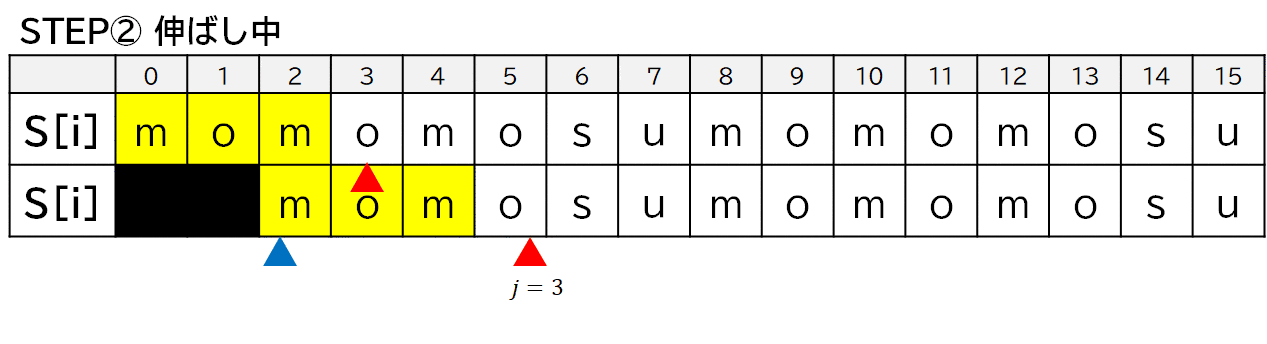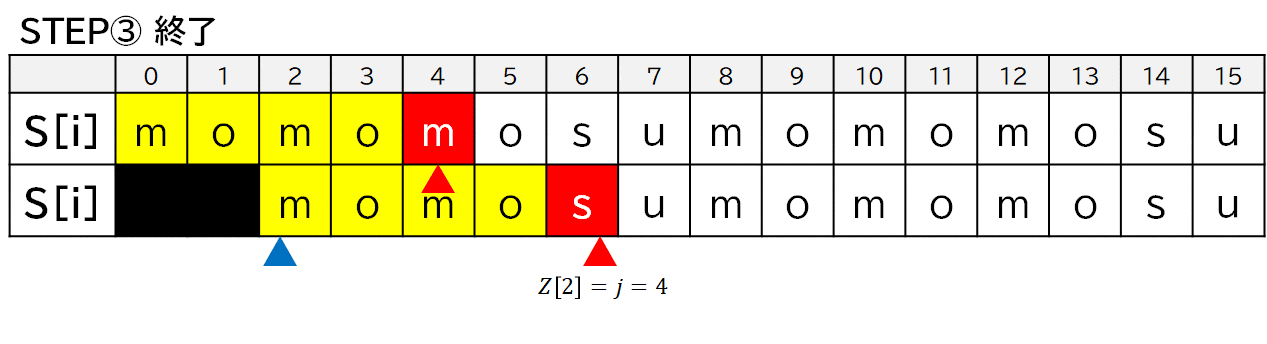
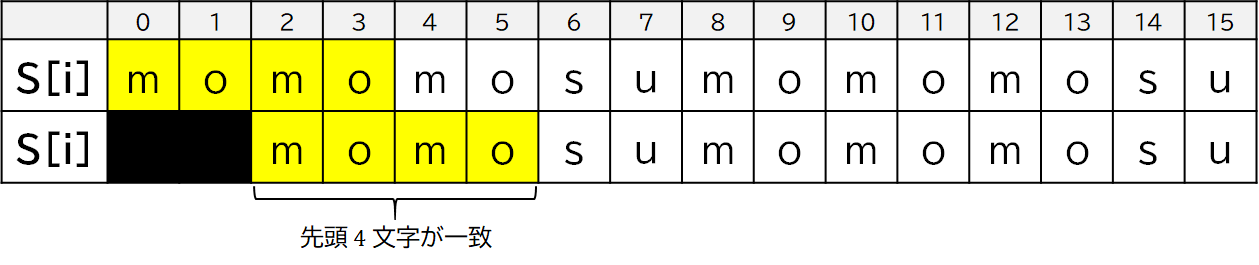
例えば，$S[2]$ 以降は momo だけ一致しているので，$Z[2]=4$ となります．

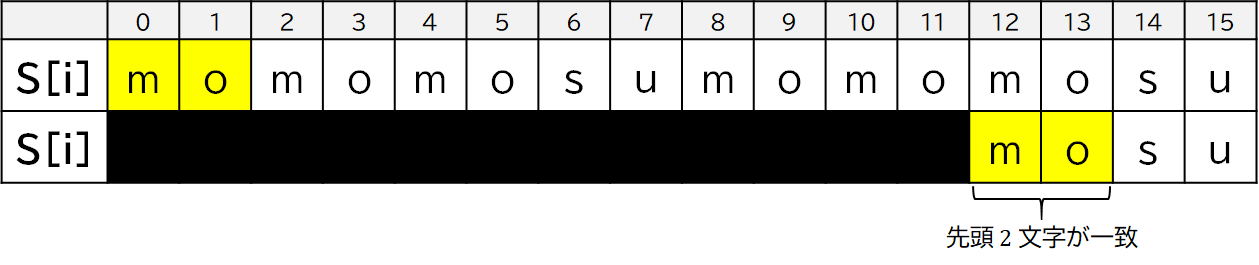
他にも，$S[12]$ 以降は mo だけ一致しているので，$Z[12]=2$ となります．

これらを各 $i$ $(0 \leq i < |S|)$ について求めた Z 配列 $Z$ は次のようになります．

ちなみに，$Z[0]=|S|$ になります．

2. 愚直な実装

$i$ の for ループを $[0,|S|)$ で回し，その中で while 文を使いながら「伸ばしていく」イメージを持って実装すると次のようになります．

Source.cpp

//string S;
//cin >> S;
vector<int> Z(S.size());
rep(i, S.size()){
    int j = 0;
    while(i + j < S.size() && S[j] == S[i+j]) j++;
    Z[i] = j;
}
//rep(i, S.size()) cout << Z[i] << " ";
//cout << endl;

なお，時間計算量は $O(|S|^2)$ です．

図解

$Z[2]$ の場合でプログラムの動きを見てみます．

3. 高速化のアイデア①

Z 配列をぐっと眺めると，何か見えてきませんか？

ぐぐぐっ・・・

この線を引いた部分，一致してませんか？　一致してます．
まあ，それはそうです．というのも，$Z[8]=8$ なので，文字列 $S[0]+\cdots+S[7]$ と文字列 $S[8]+\cdots+S[15]$ が一致しているわけです．

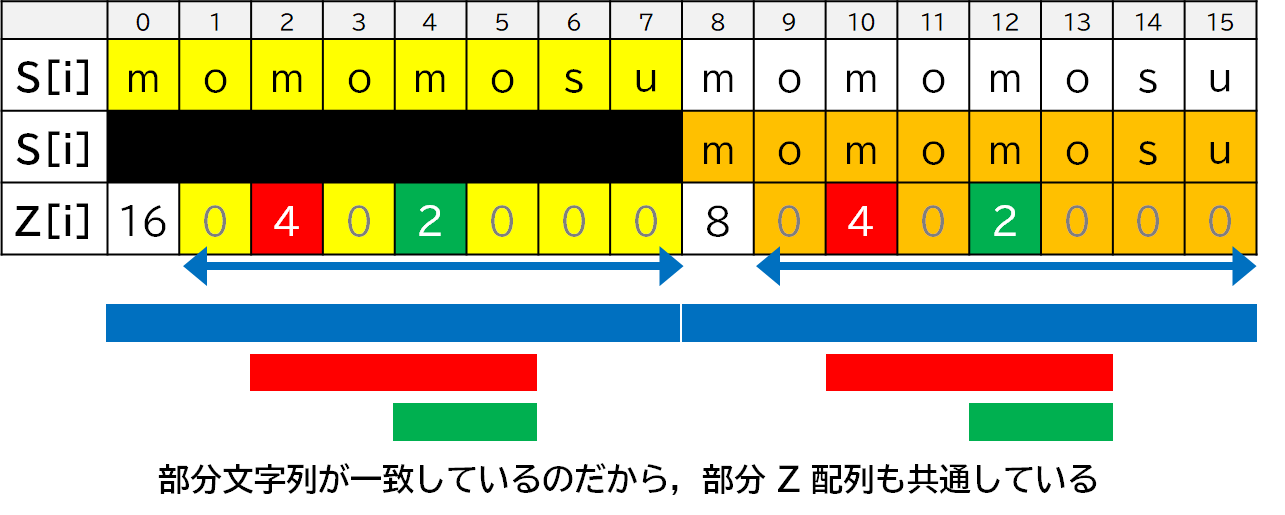
というわけで，伸びる過程で通過した部分は，2 回目以降再利用できるのです．($Z[8]=8$ と分かった時点で，$Z[9]=Z[1]=0, Z[10]=Z[2]=4,\cdots$ となる．)

と思いきや！！！　これだとバグります．

4. 高速化のアイデア②

新たな文字列**「モモもスモモも藻」**を考えてみます．

この文字列の Z 配列はこんな感じです．

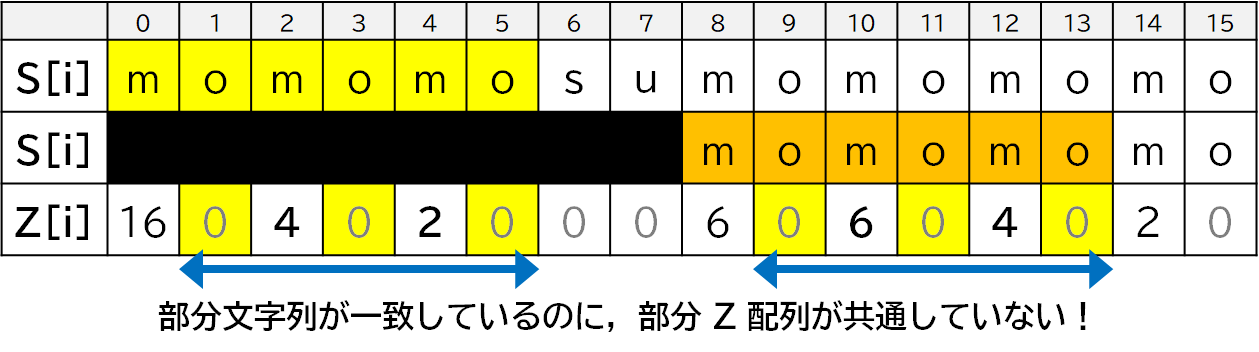
$Z[8]=6$ なので，$S[0]+\cdots+S[5]$ と $S[8]+\cdots+S[13]$ が一致しているのに，$Z[2] \neq Z[10]$，$Z[4] \neq Z[12]$ となっています．
これも，図示すれば原因がちゃんとわかります．

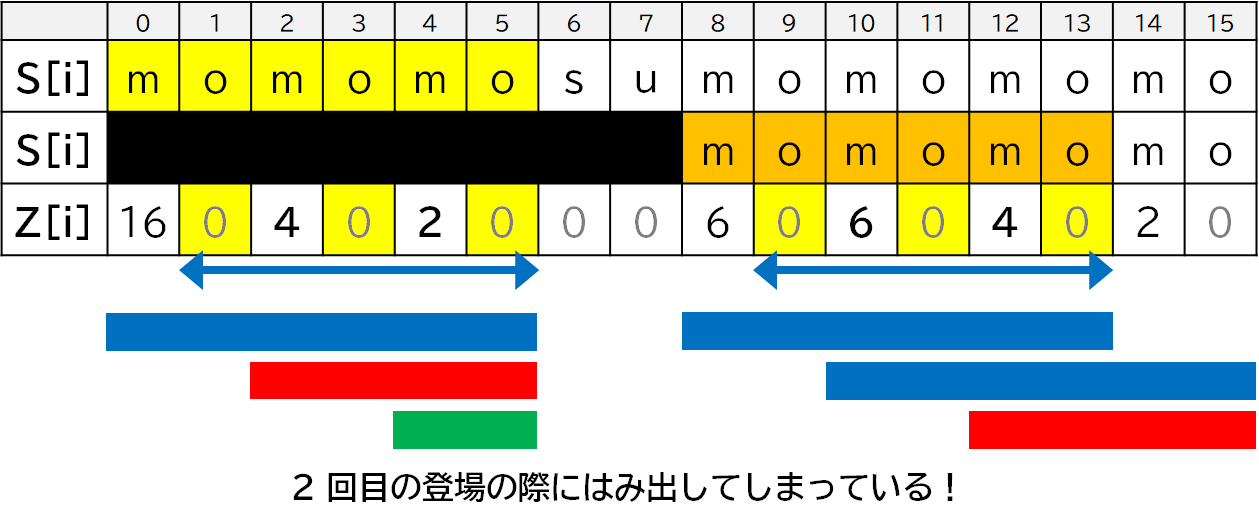
2 回目に登場した方 (オレンジの方) は，はみ出してしまっています．
具体的には，初回登場時について，「モモもスモモも酢」のときには，赤や緑の文字列が完全に青に含まれていたのではみ出しが起こらないのが確実だったのに対して，「モモもスモモも藻」のときには，赤や緑の文字列の右端が青の右端と一致していたので，はみ出す恐れが生じていました．

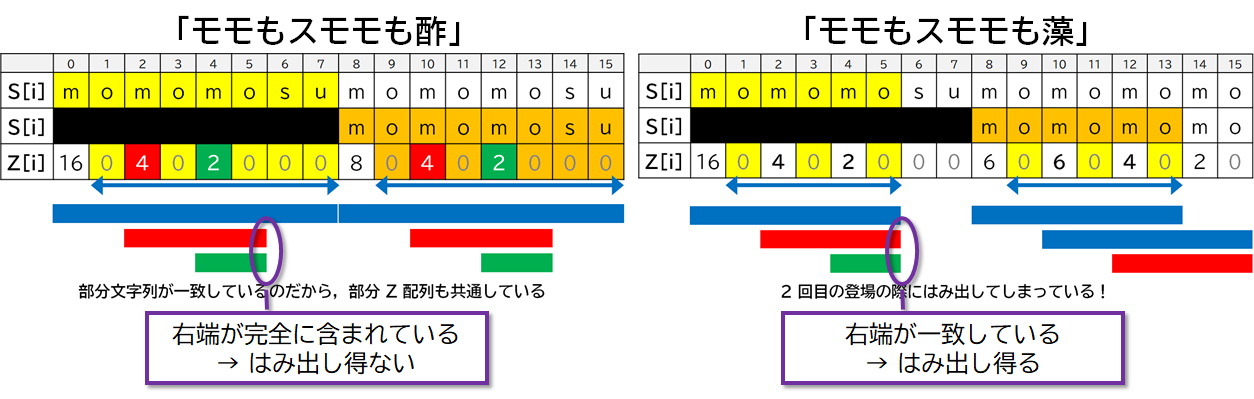
ただし，藻の場合もはみ出す恐れがあるだけで，途中まで ($S[13]$ まで) 一致していることはわかっているので，そこまでの比較処理を飛ばすことで，高速化が見込めます．

5. 高速化のアイデア③

もう一つ，文字列**「モモもヒモも草」**について考えます．

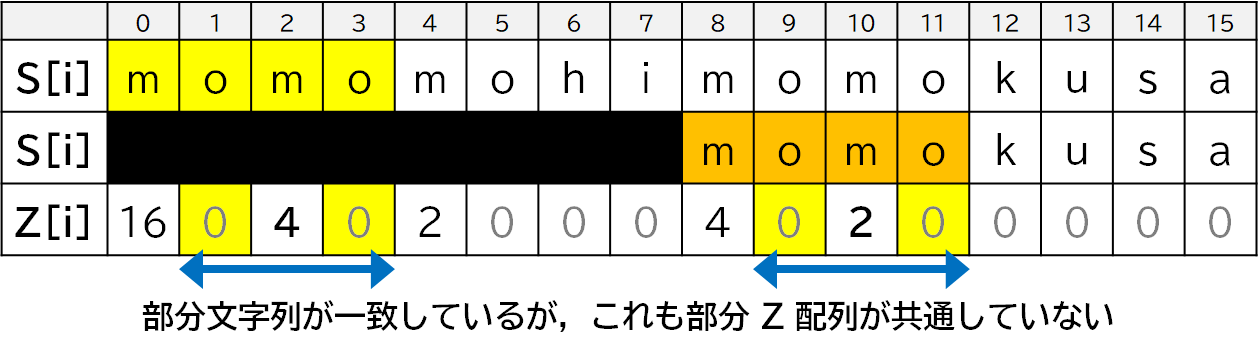
この文字列も，部分文字列が一致しているのに Z 配列が一致していない一例です．ただ，「モモもスモモも藻」とは異なることがあります．

「モモもスモモも藻」のときは 2 回目に登場したときにはみ出しが生じていたので，例えば $Z[2] < Z[10]$ となっていました．対して，「モモもヒモも草」では，$Z[2] > Z[10]$ となっています．どういうことでしょう？

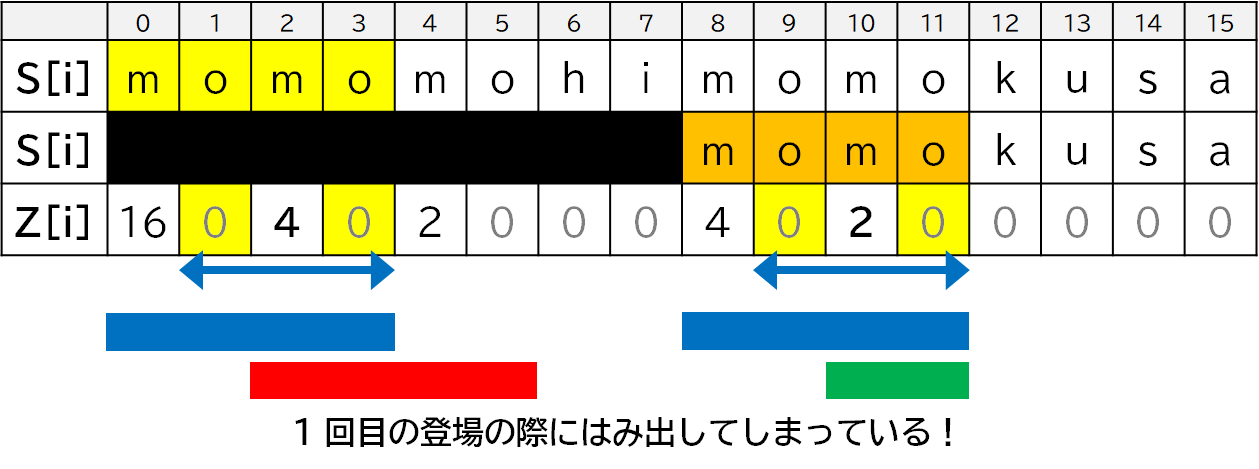
図示してみるとわかったように，今回は 1 回目の登場時にはみ出してしまっていました．当然 4 文字 ($S[8]$ から $S[11]$) 分しか一致していないので，$Z[10] = 4$ にはなりません．

この場合にも，Z 配列をそのままコピーすることはできず，どこまで一致するのか確認する必要がありますが，すでに一致することが分かっている部分は比較処理を飛ばせます．

6. 実装の方針

1. 基本は各 $i$ ごとに $Z[i]$ がいくつになるのか伸ばしながら調べます．
2. 一致しなくなってそれ以上伸ばせなくなったら，その一致している範囲について Z 値をコピーします．
3. ただし，1 回目の登場時の右端が収まっていない (一致していたり，はみ出したりしている) 場合には，そのままコピーできないので，$i$ をその位置に移動させて，探索を再開します．
4. その際，すでに一致することがわかっている部分については比較処理を飛ばします．

(実装例の後にアニメーションで再説明します．)

7. 実装例

Source.cpp

//string S;
//cin >> S;
vector<int> Z(S.size());
Z[0] = S.size();
int i = 1, j = 0;
while(i < S.size()){
    while(i + j < S.size() && S[j] == S[i + j]) j++;
    Z[i] = j;
    
    if(j == 0){
        i++;
        continue;
    }
    int k = 1;
    while(k < j && k + Z[k] < j){
        Z[i + k] = Z[k];
        k++;
    }
    i += k;
    j -= k;
}
//rep(i, S.size()) cout << Z[i] << " ";
//cout << endl;

なお，時間計算量は $O(|S|)$ です．

図解

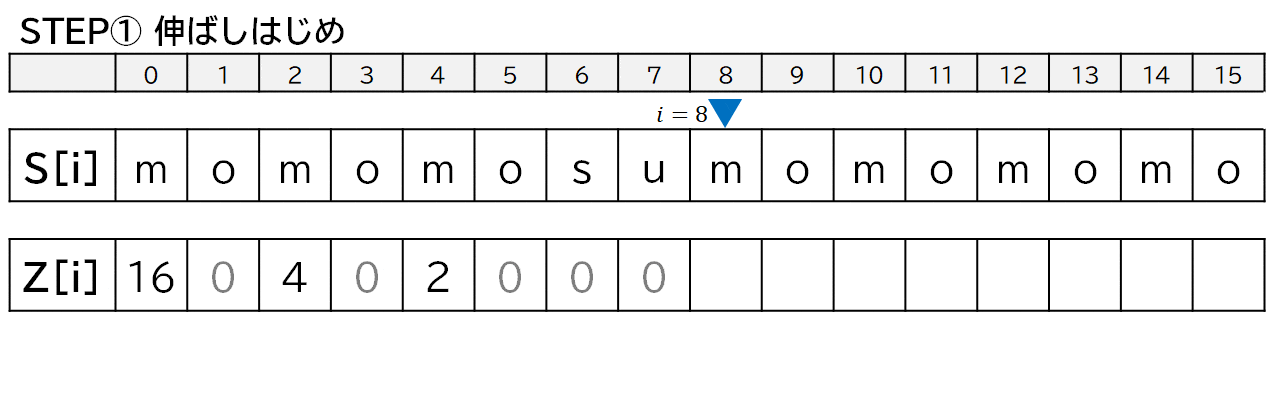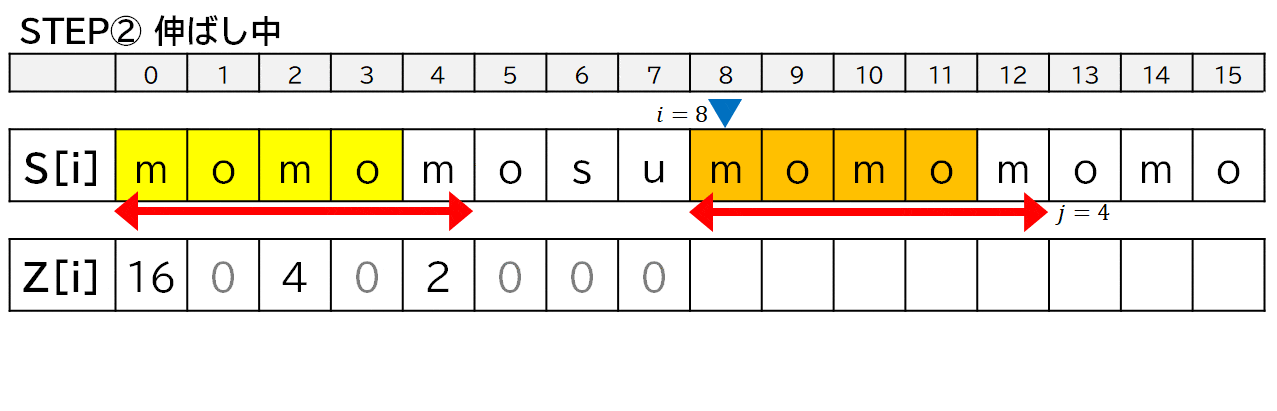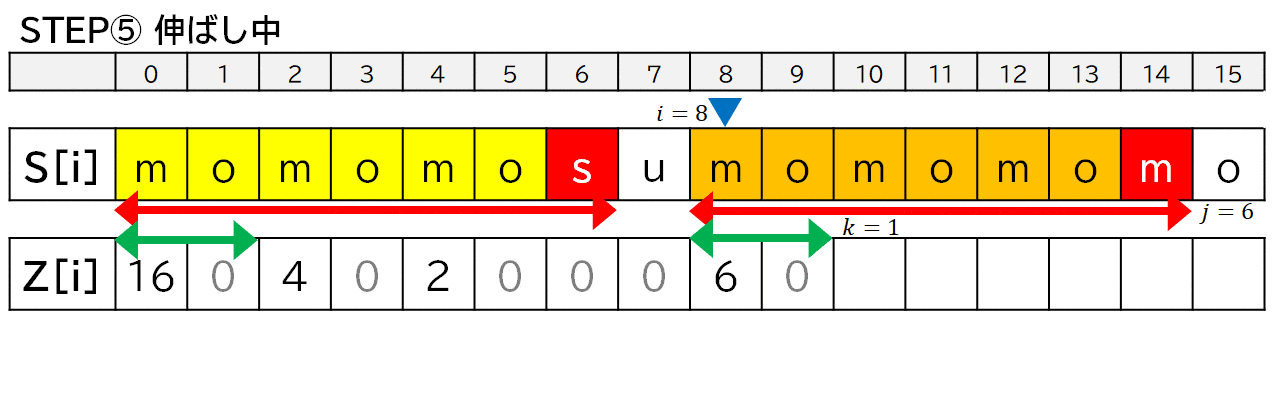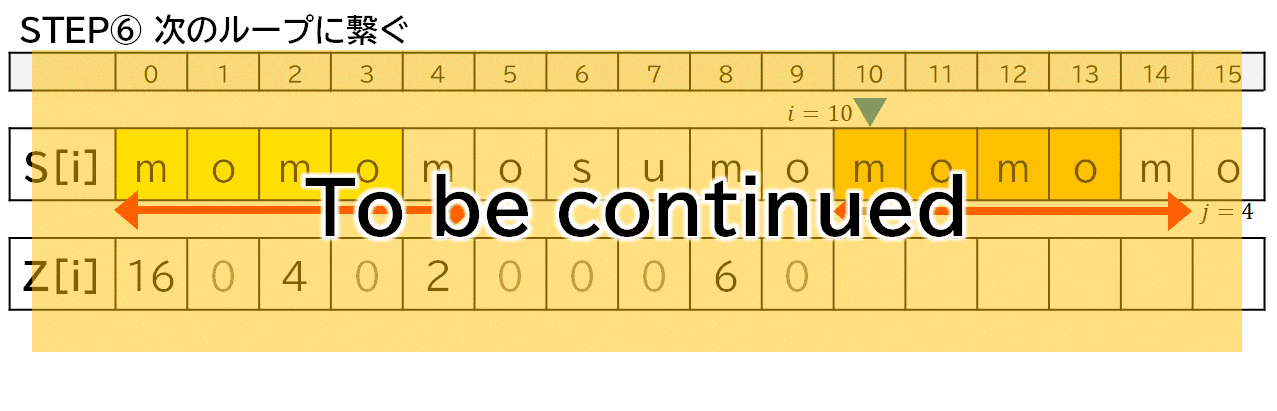
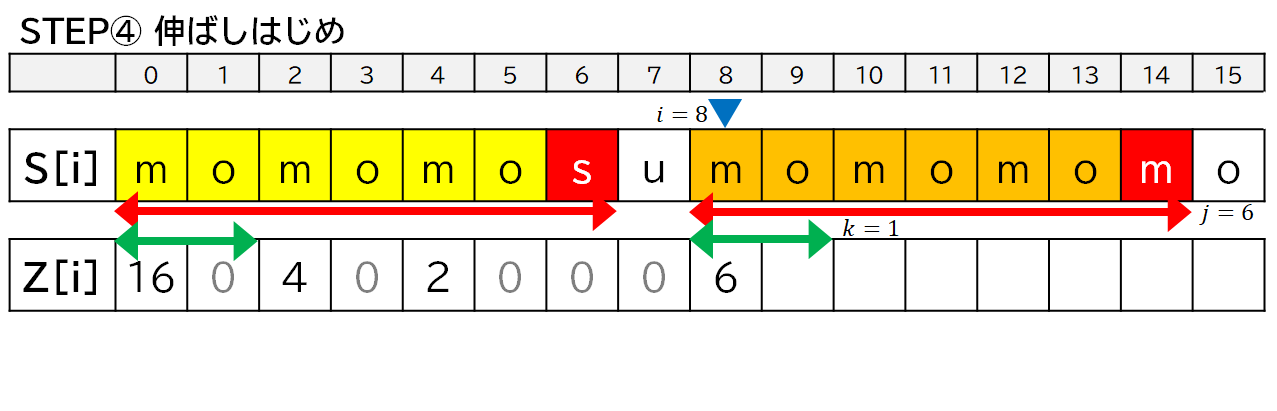
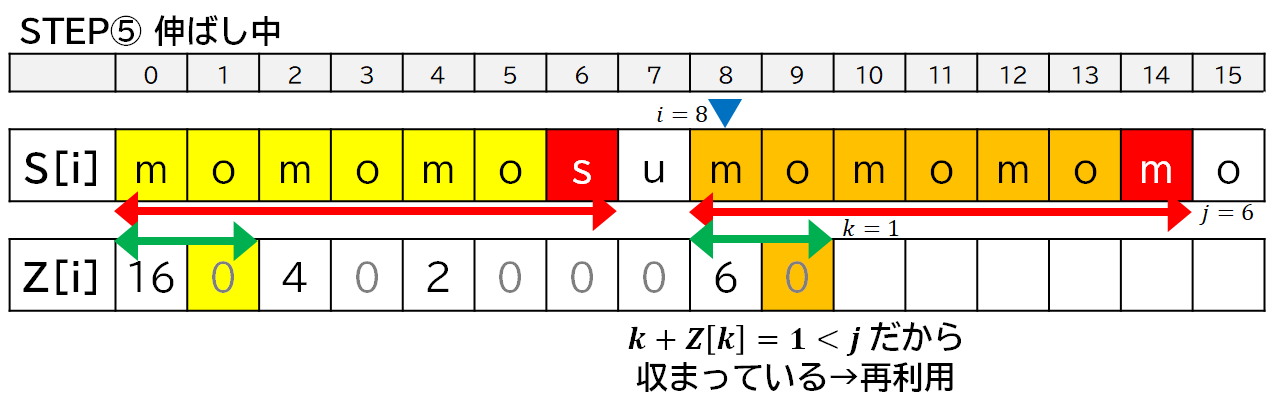
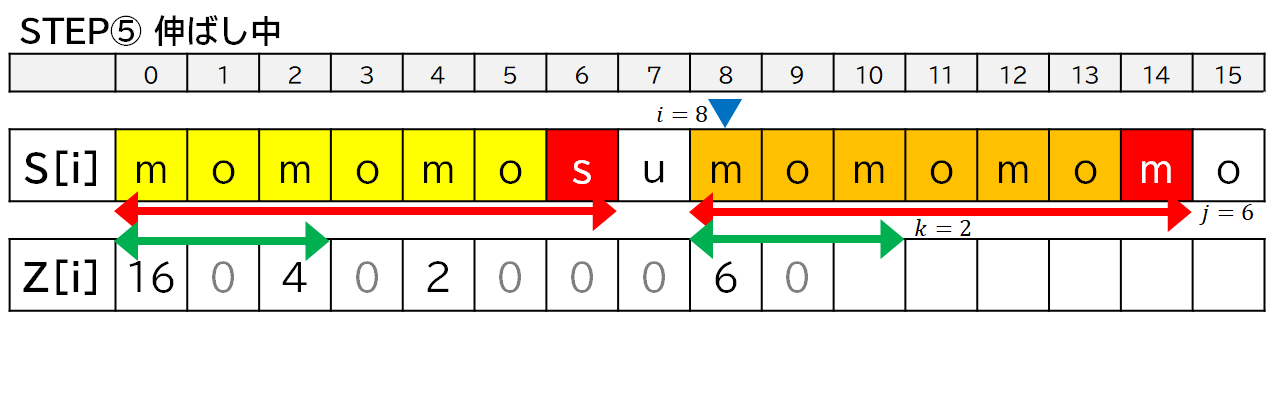
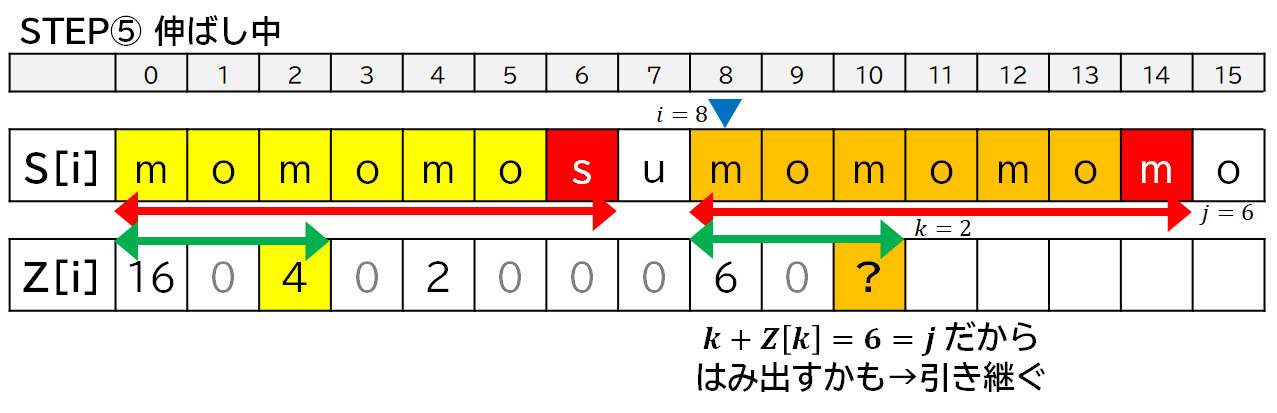
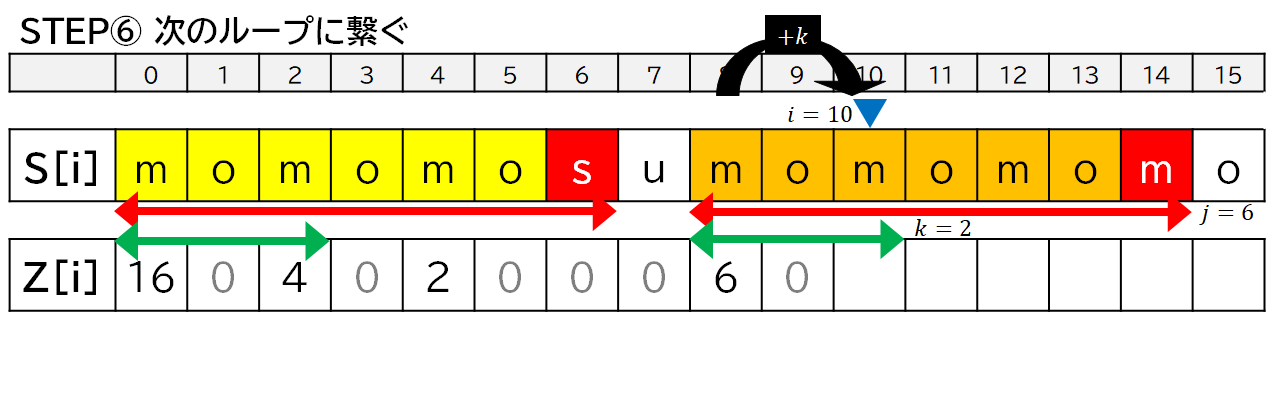
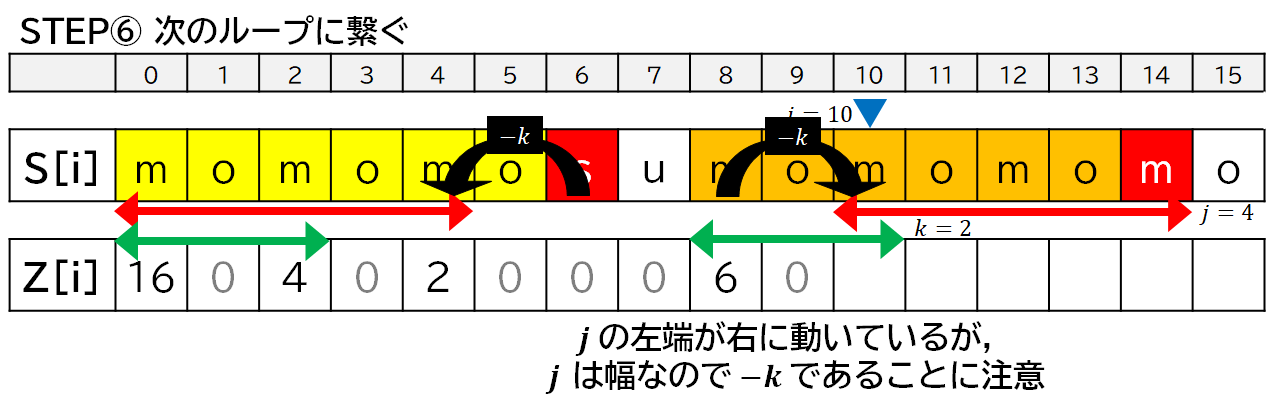
上の実装において，$i$ は位置 (マーカー)，$j, k$ は幅 ($\longleftrightarrow$) です．
「モモもスモモも藻」について，便宜上，$Z[7]$ まで求めたところからプログラムの動きを見ていきます．

バラ画像

アニメーションが速くて見逃しちゃった！という場合はこちらをどうぞ．後半部分のみ，バラ画像を置いておきます．

8. Z algorithm を使う問題

ネタバレ防止のため，畳んでいます．

• AtCoder Beginner Contest 141 E - Who Says a Pun?
• AtCoder Beginner Contest 135 F - Strings of Eternity

見かけたら適宜追加します．

9. まとめ

線形時間で最長共通接頭辞の長さたち (Z 配列) を求める文字列アルゴリズム「Z algorithm」を図とともに紹介しました．

個人的な話をすると，ABC で Z algorithm を使う典型に近い問題が出て，自分は知らなくて解けませんでしたが，水色ぐらい人が結構解けていたようでショックだったので勉強しました．そもそも文字列関連のアルゴリズムは IOI シラバスから除外されているので，あまり勉強してこなかったのです．
調べてみると割と新しいアルゴリズム¹のようで，文献が少なかったので，丁寧な解説を作ってみました．蟻本や螺旋本にも載っていないどころか，英語版 Wikipedia にすら載ってないようです．たぶん．

頑張って書いた (図を作った？) ので，じっくり読んで理解してください．ありがとうございました．

10. 参考文献

• https://snuke.hatenablog.com/entry/2014/12/03/214243 (snuke さん)
• https://scrapbox.io/pocala-kyopro/Z_algorithm (Pocala さん)

1. たぶん，Dan Gusfield さんが この本 において，1997 年に提案しました．その中身が この PDF で，ページ隅の表記の 9 ページ，PDF の 23 ページ目から Z algorithm についての記述があります． ↩