やりたいこと
以下のようなドーナツ型ポリゴンのshpファイルについて、任意の地点の内外判定を行う方法について整理しました。
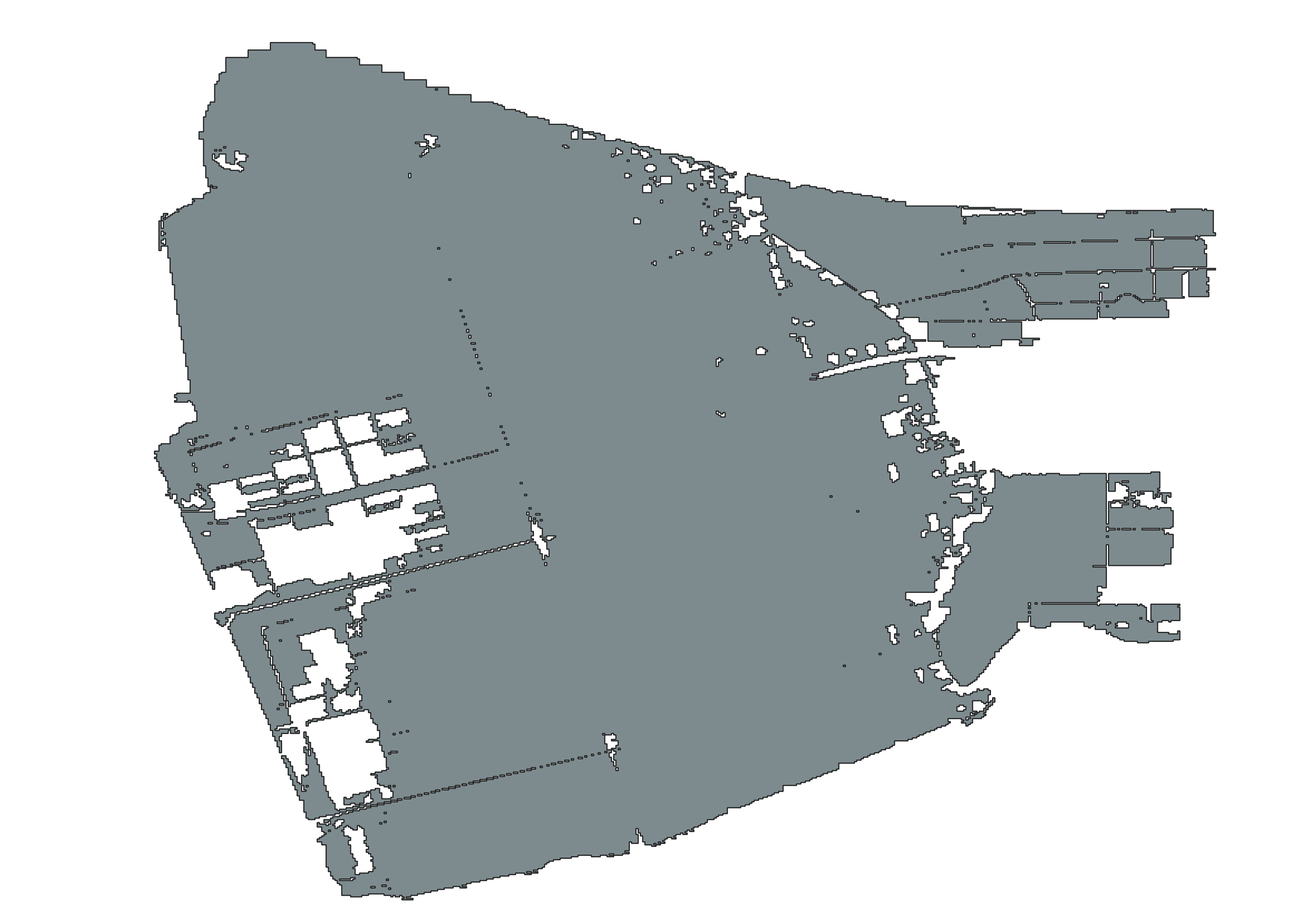
(出典:https://nlftp.mlit.go.jp/ksj/gml/datalist/KsjTmplt-A31-v2_1.html)
下記の順に解説していきます。
Step1:ドーナツ型ポリゴンデータの読み込み
Step2:内外判定モジュール
ドーナツ型ポリゴンデータの読み込み
shpファイルにおいて、ドーナツ型ポリゴンは、複数の凹凸ポリゴン(パーツ)の重ね合わせにより構築されています。したがって、まずは、各パーツの節点座標を抽出する必要があります。
import numpy
import shapefile
import matplotlib.pyplot as plt
#
def outLS(pnt,fig): #ポリゴンの節点データつなげたラインデータを描画
print(*pnt)
xs,ys = zip(*pnt)
plt.plot(xs,ys)
return 0
#
fname="test.shp" #入力ファイル
src=shapefile.Reader(fname,encoding='SHIFT-JIS') #ファイル読み込み
SRS=src.shapes() #地物情報取得
#
for srs in SRS:
IP=srs.parts #各地物のパーツを取得
NP=len(IP) #パーツの数を取得
pnt=srs.points #節点データを取得
pnts=[] #パーツ毎に、パーツの節点座標を整理
for ip in range(NP-1):
pnts.append(pnt[IP[ip]:IP[ip+1]])
pnts.append(pnt[IP[NP-1]:])
#
fig = plt.figure() #各パーツの外形線情報を描画
for np in range(NP):
outLS(pnts[np],fig)
plt.show()
plt.clf()
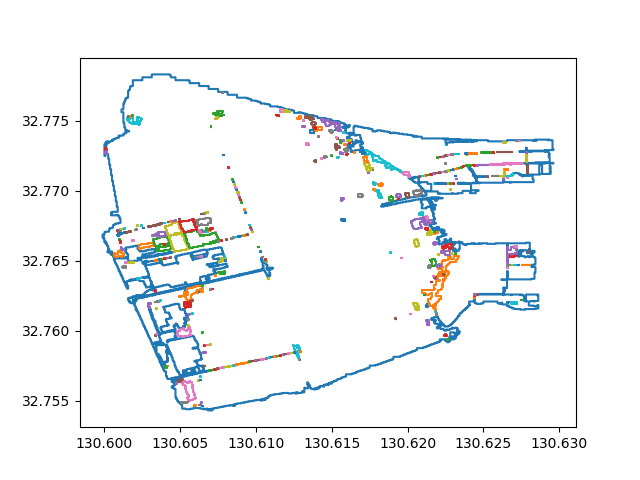
実行結果
以下のように、ドーナツ型ポリゴンを構成する各パーツの外形線情報を区別して取得できました。
内外判定モジュール
内外判定は、実は簡単です。__対象地点を始点とする半直線と、ドーナツ型ポリゴンを構成する全パーツの外形線の交差回数をチェックすればよい__です。__交差回数が奇数であれば、内側判定、偶数であれば外側判定__になります。ソースコードにすると、以下のような感じです。下の例では、対象地点から東に向かって引いた半直線と外形線の交差回数をカウントしています。
import sys
import numpy as np
import shapefile
import matplotlib.pyplot as plt
#
def naig(long,lat,pnts,boxs):
#内外判定:対象地点から東向き水平方向に半直線(=A)を引いたときに直線と地物の外形線が交差する数をカウント
NPS=len(pnts)
ccount=0
for nps in range(NPS):
pnt=pnts[nps]
box=boxs[nps]
#
if long<=box[2] and box[1]<=lat<=box[3]: #矩形を用いて交差する可能性のあるパーツを絞り込み
NP=len(pnt)
for np in range(NP-1):
xx1=pnt[np][0] #線分の始点X
yy1=pnt[np][1] #線分の始点Y
xx2=pnt[np+1][0] #線分の終点X
yy2=pnt[np+1][1] #線分の終点Y
miny=min([yy1,yy2]) #線分の最小Y
maxy=max([yy1,yy2]) #線分の最大Y
minx=min([xx1,xx2]) #線分の最小X
maxx=max([xx1,xx2]) #線分の最大X
if abs(xx1-xx2)<1.E-7: #線分が南北方向に垂直
if xx1>long and miny<=lat<maxy: #対象地点Y座標が線分の最小Y以上、最大Y未満
ccount=ccount+1
elif abs(yy1-yy2)<1.E-7: #線分がほぼ水平
ccount=ccount #水平な線分に対しては交差判定は不要
else:
aa=(yy2-yy1)/(xx2-xx1) #線分を通る直線の傾き
bb=yy2-aa*xx2 #線分を通る直線の切片
yc=lat #直線とAの交点Y座標
xc=(yc-bb)/aa #直線とAの交点X座標
#交点X座標は対象地点X座標よりも大きくなければならず、交点Y座標は線分の最小Y以上、最大Y未満でなければならない
if xc>long and miny<=yc<maxy:
ccount=ccount+1
return ccount
#
fname="test.shp" #入力ファイル
src=shapefile.Reader(fname,encoding='SHIFT-JIS') #ファイル読み込み
SRS=src.shapes() #地物情報取得
SRR=src.shapeRecords() #地物情報取得
#
# 地物情報を取得
pntall=[]
for srs in SRS:
IP=srs.parts #各地物のパーツを取得
NP=len(IP) #パーツの数を取得
pnt=srs.points #節点データを取得
pnts=[] #パーツ毎に、パーツの節点座標を整理
for ip in range(NP-1):
pnts.append(pnt[IP[ip]:IP[ip+1]])
pnts.append(pnt[IP[NP-1]:])
pntall.append(pnts)
#
# 属性情報を取得
recall=[]
for srr in SRR:
recall.append(srr.record)
if len(pntall)!=len(recall):
print("属性情報の数と地物の数の不一致!!")
sys.exit()
#
# 各パーツを包有する矩形を求めておく(矩形情報取得)
NPA=len(pntall) #地物数
boxall=[]
for npa in range(NPA):
pnts=pntall[npa]
NPS=len(pnts) #パーツ数
boxs=[]
for nps in range(NPS): #各パーツの節点の緯度、経度の最小値・最大値を取得
pp=np.array(list(pnts[nps]),dtype=np.float32)
bbox=[pp[:,0].min(),pp[:,1].min(),pp[:,0].max(),pp[:,1].max()]
boxs.append(bbox)
boxall.append(boxs)
#
# 交点数をカウントする
LON=[130.60533882626782543,130.59666405110618825,130.60918282680634661,130.60550819793903088,130.60379578346410767]
LAT=[32.76515635424413375,32.77349238606328896,32.77375748954870716,32.76751282967006063,32.77819292046771693]
NPP=len(LON) #地点数
for npp in range(NPP): #地点についてのループ
for npa in range(NPA): #地物についてのループ
ic=naig(LON[npp],LAT[npp],pntall[npa],boxall[npa])
if ic % 2==0: #外側にある場合
print("地点{0}は地物{1}の外! (交差数:{2})".format(npp+1,npa+1,ic))
else: #内側にある場合
print("地点{0}は地物{1}の中! (交差数:{2})".format(npp+1,npa+1,ic))
実行結果
以下のように、判定できました。内外判定は、sympyを用いる方法よりも、こちらの自作モジュールの方が大分早そうです。
地点1は地物1の外! (交差数:14)
地点2は地物1の外! (交差数:18)
地点3は地物1の中! (交差数:3)
地点4は地物1の外! (交差数:4)
地点5は地物1の中! (交差数:1)