ニュートン法とは
ニュートン法とは、f(x)=0になるようなxを求めるアルゴリズムの1つで、方程式の解を近似的に求めることができる方法です。
ニュートン法を用いると、√2の値やsin(x)=0.5になるようなxの値など近似的に求めることができます
ニュートン法の考え方
ニュートン法では、以下の考え方に基づいて計算が行われます
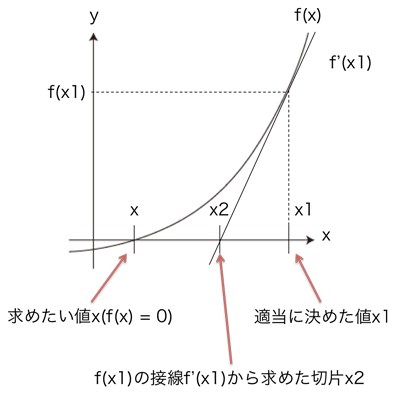
f(x) = 0になるような値xを探す時、ある値x1における接線の切片x2は、元の値x1より真の値xに近くなる
この考え方は下の図のように、f(x)という関数においてf(x) = 0になるようなxを求めたいとき、ある値x1における接線f'(x)の切片x2を求めると、求めたい値xに対して、x1よりもx2の方が近くなるということを意味しています
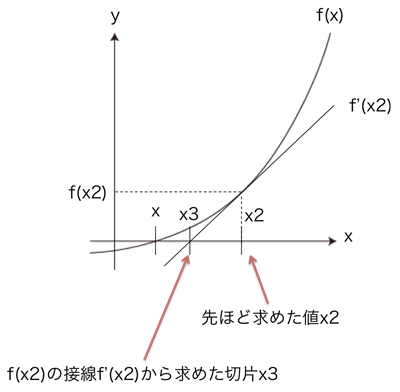
先ほど算出したx2の値を元にして同様の操作を行うと、x3は目的となる値xにより近づきます
この手順を繰り返せば繰り返すほど、算出される切片の値は目的となる値xに近づいていきます
具体的な計算方法
x1からx2,x3を求める手順を示し、そこから一般的な関係式について算出します
x1からx2を算出する
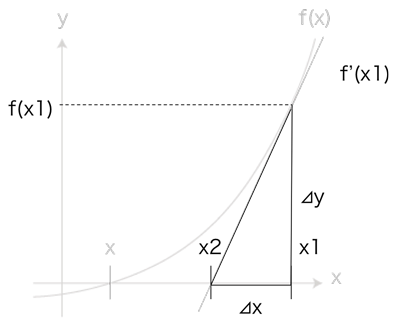
下の図のようにx1, x2, f(x1)で作られる直角三角形に注目します。⊿x, ⊿yはそれぞれ直角三角形の辺の長さを表します
f'(x1)はf(x1)における接線なので、傾きの定義式の関係より、x2を求めることができます
\begin{aligned}
f'(x_1)&=\frac{\Delta y}{\Delta x} \\
&=\frac{f(x_1)}{x_1 - x_2} \\
\Leftrightarrow x_1-x_2&=\frac{f(x_1)}{f'(x_1)} \\
\therefore x_2 &=x_1 - \frac{f(x_1)}{f'(x_1)}
\end{aligned}
同様の手順を用いてx3についてもx2から算出することができます
\begin{aligned}
x_3 &=x_2 - \frac{f(x_2)}{f'(x_2)}
\end{aligned}
つまり、今ニュートン法をn回行って算出したx座標xnに対してニュートン法を適応して算出されるx座標xn+1には次のような関係式が成り立ちます
\begin{aligned}
x_{n+1} &=x_n - \frac{f(x_n)}{f'(x_n)}
\end{aligned}
計算回数nを増やしていけば行くほど、xnは真の値xに近づいていきます
計算例(√2を求める)
ニュートン法についてはなんとなくの理解をすることができたと思いますが、実際にどうやって使うのかということを実際の計算例を通して理解を深めます
ここでは、√2の値について求めてみたいと思います。
まず、√2の値はわからないのでxとおきます
x=\sqrt{2}
計算がしやすいようの両辺を2乗し、f(x)=0となるように式変形を行います
\begin{aligned}
x^2 &= 2 \\
x^2-2 &= 0 \\
f(x) &= 0 \hspace{1em} (\therefore f(x) = x^2 - 2)
\end{aligned}
ニュートン法の関係式について当てはめると次の様になります
\begin{aligned}
x_{n+1} &= x_n - \frac{f(x_n)}{f'(x_n)} \\
&= x_n - \frac{x_{n}^2-2}{2x_n}
\end{aligned}
ここでx1の値を適当に5と仮定して計算を行ってみます
\begin{aligned}
x_2 &= x_1 - \frac{x_{1}^2-2}{2x_1} \\
&= 5 - \frac{5^2 -2 }{2 \times 5} \\
&= 2.7
\end{aligned}
n=5になるまで同様に計算を行ってみます
\begin{aligned}
x_3 &\risingdotseq 1.720 \\
x_4 &\risingdotseq 1.441 \\
x_5 &\risingdotseq 1.414
\end{aligned}
√2の真の値は1.414...となるので、計算回数を増やすほど真の値へと近づいていくことが分かります
プログラムで書くニュートン法
上記で書いたように√2の値を求めるプログラムを以下に紹介します。プログラムの内容を理解しやすいという観点からPython3を用いてプログラムを記述します
# 適当な初期値の設定
x = 5.0
while True:
# ニュートン法による新しいxを求める
x2 = x - (x * x - 2) / (x * 2)
# 計算後の値が誤差の範囲内になったら計算終了
if abs(x2 - x) < 0.0001:
break
# 計算後の値をxとして計算を繰り返す
x = x2
# 計算結果の表示
print(x)
x = 5.0
初期値を5ではなく5.0とすることで、小数点以下の結果も変数に確保します
x2 = x - (x * x - 2) / (x * 2)
前節で求めた方程式より、真の値に近くなるxの値を計算します
if abs(x2 - x) < 0.0001
計算を繰り返し行なっていくと、解が真の値に近づいていくので、値の変化が小さくなっていきます。そこで、誤差を設定して値の変化量が誤差の範囲内なったところで計算を終了します。
まとめ
ニュートン法とはf(x)=0となるxを求めるための手法で、繰り返し計算を行うことでxについて近似的に算出することができます。また、誤差範囲を指定することで、有効桁数が保証された値を得ることができます