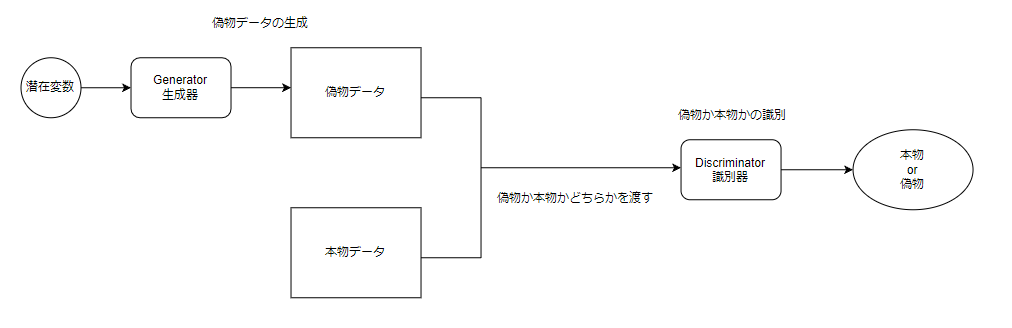
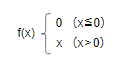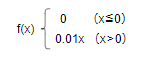GANとは
GAN(Generative Adversarial Networks)は敵対的生成ネットワークとよばれます。
生成器と識別器と呼ばれる二つの人工知能を互いに競わせるようにすることで、画像や小説、音楽などのデータ分布を模倣するディープラーニングモデルです。
二つの人工知能の役割としては以下のようになります。
- 生成器:データ分布を生成する
- 識別器:本物か生成器が生成した偽物かを識別する
生成器は偽札を作成する偽造者で、識別器は偽札かどうかを識別する警察
などのような、たとえ方をされることが多いです。
生成器は識別器をだませるような偽物を生成するように学習し、識別器は偽物かどうかを正確に予測するように学習します。
このように、互いに競いながら学習させることから敵対的生成ネットワークと呼ばれています。
生成と識別器のうちGANとして必要なのは生成器のほうです。
生成器を用いて、この世に存在しない画像や小説、音楽などを生成します。
構成
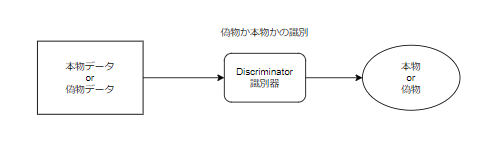
識別器
識別器の役割は偽物か本物かを正確に判別することです。
学習では本物かどうかを正確に見分けられた確率をもとに学習していきます。
入力:本物か偽物のどちらか
出力:本物かどうかの確率(0に近いほど偽物確率が高く、1に近いほど本物の確率が高い)
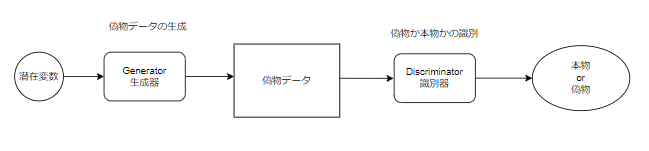
生成器
生成器の役割は識別器をだませる偽物を生成することです。
学習では以下のように生成した偽物を識別器が本物と判断した確率をもとに学習していきます。
入力:潜在変数
出力:偽物データ
潜在変数
潜在変数とは生成器が画像を生成するための種になる変数のことです。
一般的に100次元の変数で正規分布から抽出します。
損失関数
GANの損失関数は以下の式になります。
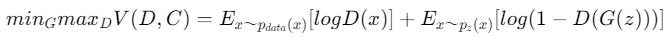
一見難しく感じますが、生成器、識別器が何を目的としているかについて着目するとそこまで難しくはありません。
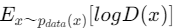
本物データ($p_{data}$)に対して識別器(D(X))をかけた値に対して対数をとります。(logD(x))
識別器が
- 本物(1)と判断すると値が最大になります。
- 偽物(0)と判断すると値が最小になります。
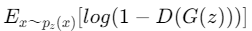
偽物データ($p_{data}$)に対して、1から識別器(D(X))をかけた値を引いた値に対して対数をとります(log(1-D(G(z)))
識別器が
- 本物(1)と判断すると1-1=0で値が最小になります。
- 偽物(0)と判断すると1-0=1で値が最大になります。
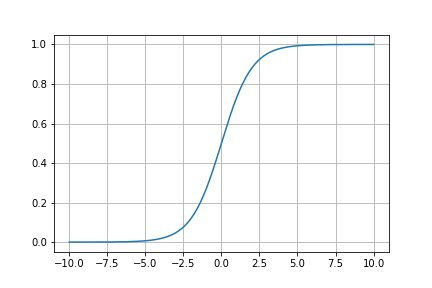
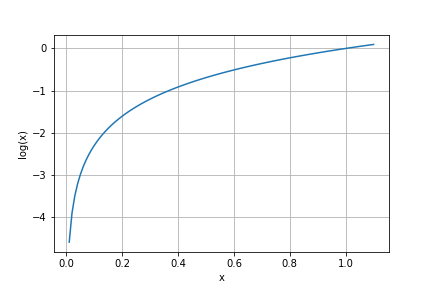
対数について
対数のグラフは以下のようになります。
Dの出力は本物かどうかを0~1で表現します。
識別器
識別器の役割は偽データか本物データかを見分けうことが役割としてあります。
目的としてはできる限り高い精度で本物かどうかを見分けることとなります
そのため、損失関数の値が最大になるように学習します。
生成器
生成器の役割は識別器をだませるような本物データに近い偽物データを生成することが役割としてあります。
目的としてはより本物に近いデータを生成し、識別器の騙し精度が低くなるようにすることとなります
そのため、損失関数の値が最小になるように学習します。
また、生成器はより本物に近いデータを生成し識別器の騙すことが目的のため、学習時には本物データを使用する必要はありません。
そのため、右辺第一項は損失値を計算するときには使用しません。
DCGANとは
DCGAN(Deep Convolutional Generative Adversarial Networks)は深層畳み込み敵対的生成ネットワークと呼ばれ、GANに対して、CNNを適用することでより高精度の画像生成を可能にします。
DCGANには学習を安定的に行うために以下のような指針が存在します。
- 畳み込み層、転置畳み込み層どちらの場合にもストライドは2のものを使用する
- 生成器の出力層、識別器の入力層以外の層でバッチ正規化を行う
- 全結合層は用いず、畳み込み層のみを使用する
- 識別器の活性化関数は出力層ではSigmoid関数を使用し、それ以外ではLeakyReLUを使用する
- 生成器の活性化関数は出力層ではTanh関数を使用し、それ以外ではReLU関数を使用する
- 識別器の訓練時に偽物と本物はバッチ内で混ぜて学習を行わない。
(バッチ正規化層でまとめて正規化されてしまう恐れが存在するため) - 生成器の損失関数を$min_G[log(1-D(G(z)))]$ではなく$max_G[log(D(G(z)))]$とする
畳み込み層
畳み込み層では、配列に対してフィルターを通して別の配列に変換する処理を行います。
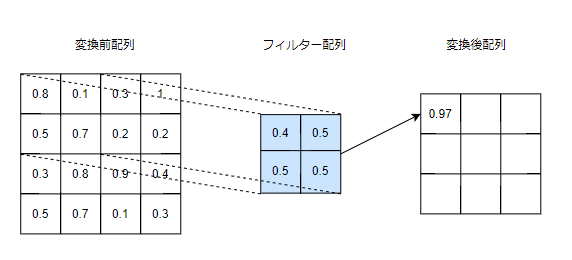
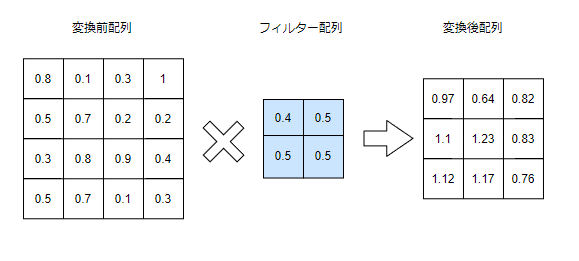
転置畳み込み層
転置畳み込み層では、変換前配列のサイズを増やしてから畳み込み処理を行います。
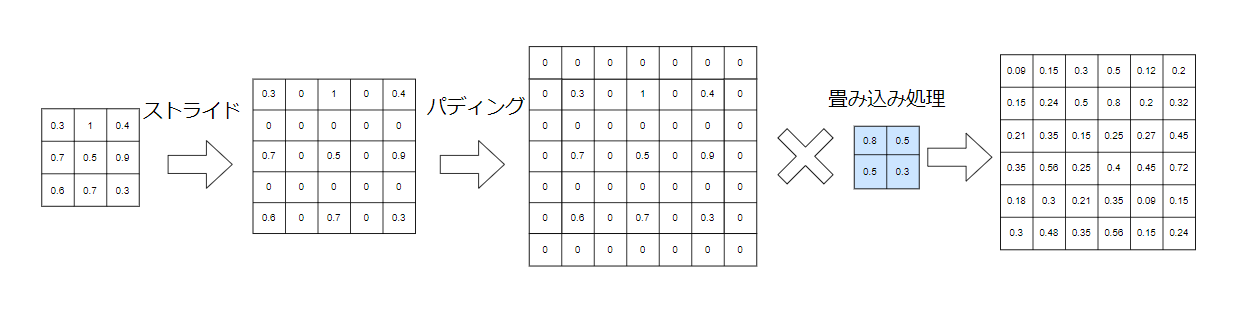
バッチ正規化
バッチごとに平均0、分散1になるように正規化を行います。
バッチ正規化を行うことで、データの分布が標準正規分布に従うようになり、
隠れ層の間に挟むことで学習速度の向上や安定化につながります。
活性化関数
Sigmoid関数
$f(x) = \frac{1}{1+e^{-x}}$
0~1の範囲で値を出力します。
この0~1の値を確率として表現して二値分類問題の出力層にはほぼ必ず使用されます。
今回は識別器の出力層として本物である確率を表現するために使用されます。
Tanh
数式は以下の通りです。
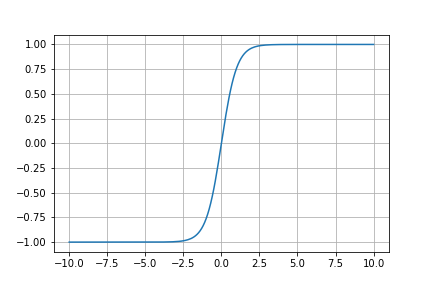
$f(x) = \frac{e^x - e^{-x} }{e^x + e^{-x}}$
-1~1の範囲の値を出力します。
今回は生成器の出力層に使用します。
画像のスケーリングされた範囲[-1~1]を表現するために使用します
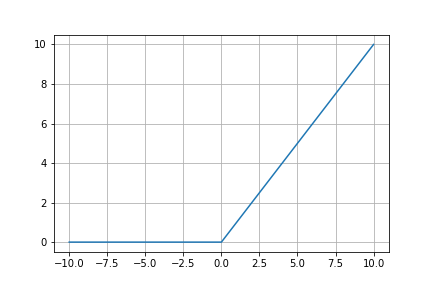
ReLU
0もしくは入力値をそのまま出力する非常に単純な関数です
出力
- 入力(x)が0以下の場合には0を出力
- 入力(x)が0以上の場合にはxを出力
特徴
- 数式が単純なため計算速度が速い
- シグモイド関数と比べ勾配消失問題が起きにくい
- 0以下の場合には0を出力することでスパース性の再現可能にはつながるが
同時に勾配消失問題も起きやすくなってしまう
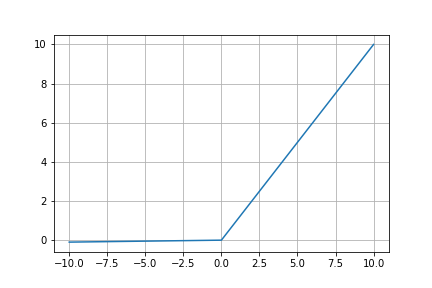
LeakyReLU
ReLU関数を改良したのがLeakyReLU関数です。
ReLU関数との違いとして0以下の出力の場合にxに0.01かけた微小な値を出力するといった点が異なります。
グラフではわかりにくいですが、0以下の場合、微小に値が傾いています。
0以下の出力の場合に微小な値を出力することで勾配が消失しないようになります。