[最新論文] 新しい最適化手法誕生! AdaBound & AMSBound

#論文紹介　画像引用

https://openreview.net/pdf?id=Bkg3g2R9FX
https://github.com/Luolc/AdaBound
https://www.luolc.com/publications/adabound/

#AdaBoundとAMSBound
Adamに学習率の上限と下限を動的に加えたものをAdaBound

AMSGradに学習率の上限と下限を動的に加えたものをAMSBound

どちらの手法も最初はAdamのように動き、後半からSGDのように動く

Adamの良さである初期の学習の速さとSGDの良さである汎化能力を両立した最適化手法

#Adamの問題点
SGDと比べて汎化性能が劣る・未知のデータに弱い

不安定で極端な学習率を使うため上手く収束しない

##AMSGrad
こういったAdamの問題を解決しようとしてできたのがAMSGrad
http://www.satyenkale.com/papers/amsgrad.pdf

AMSGradは悪い性能の原因になっている大きすぎる学習率を改善したが、
小さい学習率も悪い性能につながるという事実を考慮していないため優れた最適化手法にはならなかった

実際、AMSGradはAdamとほぼ同等の性能にとどまることが最近の研究でわかった

本研究では大きすぎる学習率だけでなく小さすぎる学習率も汎化能力に悪い影響が出ることを立証していく

##収束に近いときの学習率はどうなっているのか？

サンプルされたパラメーターの学習率
数値は対数演算されている（$log_e0.01=-4.6 ,; log_e1000=6.9$）
薄い色は小さい学習率、濃い色は大きい学習率を意味する

###実験
データはCIFAR-10、最適化はADAMを使ったResNet34から
重みとバイアスをサンプリングして学習率を見てみる

①異なる層から9つの3×3カーネルを選び、最終線形層からバイアスを選ぶ
②同じ層のパラメーターは同じ特性があるため、9つのカーネルからそれぞれ１つずつ選んだ合計9つの重みの学習率と最終層の1つのバイアスの学習率を見る

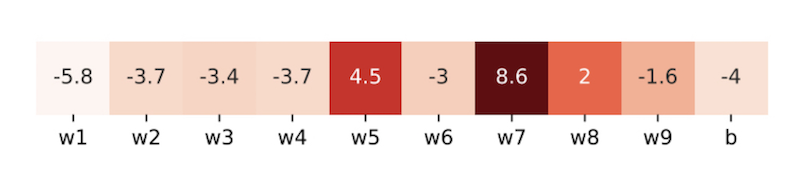
上図が示すように収束が近くなると学習率は0.01以下の小さすぎる値になったり1000以上の大きすぎる値になったりしてしまう

$log_e0.01=-4.6 ,; log_e1000=6.9$であることを考えると、
$w1$の学習率は$0.01$よりも小さく、$w7$の学習率は$1000$よりも大きいということがわかる

##Adamは最適解から遠ざかっていく
小さすぎる学習率が原因で上手く収束しない例を示す

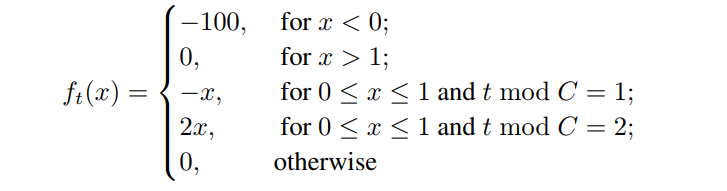
$C$は　$5β_2^{c-2} \leqq(1-β_2)/(4-β_2)$を満たす

$t; mod;C$は$t$を$C$で割ったときの余りを意味する
例）$t=5,C=3$のとき、$t; mod;C=2$

上の場合分けを見ると、$x<0$のときが最適解なのは明らかである

しかし$β_1=0$としたAdamでは$x\geq0$の局所解に陥って収束してしまう
なぜそうなるかは以下のようになるためである
C=3のように具体的に考えた方がわかりやすいと思う

###Adamが局所解に収束する流れ
①アルゴリズムは$C$ステップに$1$回、$-1$の勾配を得る
勾配の逆方向に進むのが最適化のため、
-1の勾配を受けとった時は最適解とは逆方向に進んでしまう（最適解は$x<0$）

②その次のステップで2の勾配を得る
2の勾配（正しい方向）を得たにも関わらず、前回の逆方向に進んだものを打ち消すような働きをすることはできない

これは、ステップが進むごとに学習率が小さくなるというAdamの性質によるものである

正しい方向に進むための絶対値の大きい勾配を得ても学習率の性質上、理想的な動きをしてくれない

→　$x$はステップを重ねるたびに大きくなってしまう（最適解から離れてしまう）

また、$\beta_1<\sqrt\beta_2$を満たす任意の$\beta_1,\beta_2\in[0,1]$、任意の初期ステップサイズ$\alpha$を選択してもAdamは最適解に収束できない例があることがわかった

###SGDだったらどうなるのか？

SGDの学習率は一定であるため（$α_t=α$）、
このような問題に陥らずに最適解に行くことができる可能性が十分ある

#AdaBoundとは？
Adamの学習初期の学習の速さとSGDの汎化能力を組み合わせたような最適化手法があれば理想
＝学習前半はAdamのように動き、学習後半からはSGDのように動くもの

勾配クリッピング（勾配爆発を防ぐために、勾配が閾値を超えないようにする手法）のアイデアを応用して使う

Adamの学習率をクリッピングしたものをAdaBoundとする

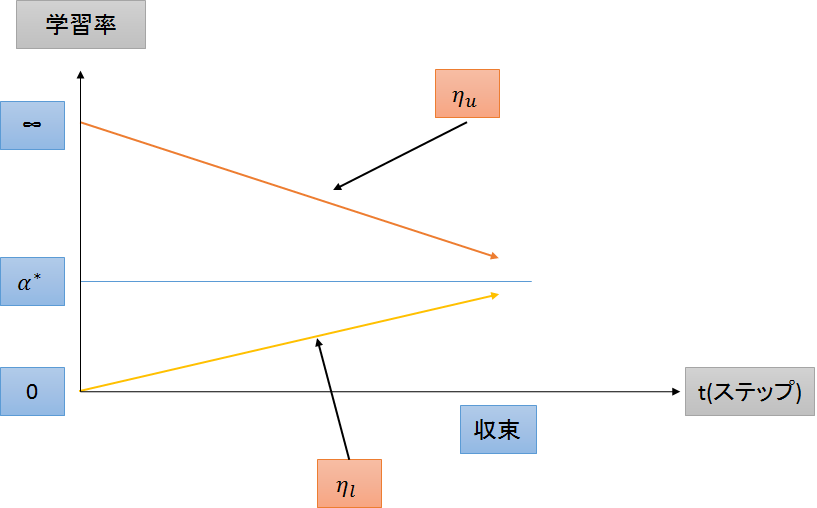
##学習率の動き

学習率の範囲を$[\eta_l,\eta_u]$とすると
$\alpha=\alpha^{*}$ のSGDは$\eta_l=\eta_u=\alpha^{*}$であると考えることができる
Adamで言うならば、$\eta_l=0,\eta_u=\infty$

ステップ$t$に応じて$\eta_l$と$\eta_u$を変化させていく
前半はAdam、後半はSGDのような動きができている

上図はイメージであり、論文内の実験では
$\eta_{l}(t)=0.1-\frac{0.1}{(1-\beta_2)t+1},;\eta_{u}(t)=0.1+\frac{0.1}{(1-\beta_2)t}$を使った
$\beta_2=0.999$とすると初期の下限が$0$で上限が$0.2$と考えられる

###学習率の下限
$\eta_{l}(t)$は$t=0$のとき$\eta_l=0$から始まり、$\eta_l=\alpha^*$に近づいて収束する

###学習率の上限
$\eta_u(t)$は$t=0$のとき$\eta_u=\infty$から始まり、$\eta_u=\alpha^*$に近づいて収束する

#AMSBoundとは？
AdaBoundに行った学習率の制限を同じようにAMSGradに組み入れたもの

AMSBoundはAdaBoundと同等の優れた性能を持つ

#本研究の良いところ
以前にもAdamからSGDへの移り変わりというアイデアはあったが、本研究の移り変わりには良いところが以下のように2点ある

##①AdamからSGDに徐々に移り変わっていく

・何ステップ目でAdamからSGDに切り替えるという考えではなく、
徐々にAdamからSGDに移り変わっていく
・ハードな変化ではなく、ソフトな変化ということができる

##②切り替えのためのハイパーパラメーターがいらない
これまでの同様の研究では何ステップ目で切り替えるかを決めるために追加のハイパーパラメーターを用意していたが、この調整は簡単ではない

#AdaBoundとAMSBoundはハイパーパラメーターの選択に対してロバスト
何ステップ目でAdamからSGDに切り替わるか（更新式の$\beta$を大きくすると切り替わりが遅くなる）と
最終学習率$\alpha^*$の設定をいくつにするかはそれほど重要ではないということも本研究の実験を通してわかった

以下のようにハイパーパラメーターの選択を変えても安定して優れた性能を示した

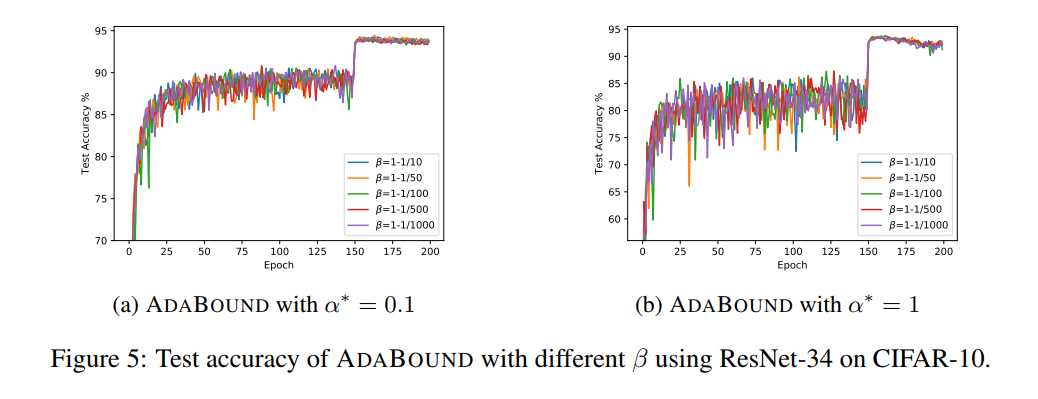
$\alpha^*=0.1$のときと$\alpha^*=1$のとき、それぞれで$\beta$の値を変えて検証したもの

$\beta$の値（AdamからSGDに移り変わる速度）がいくつであっても安定して高い精度だった

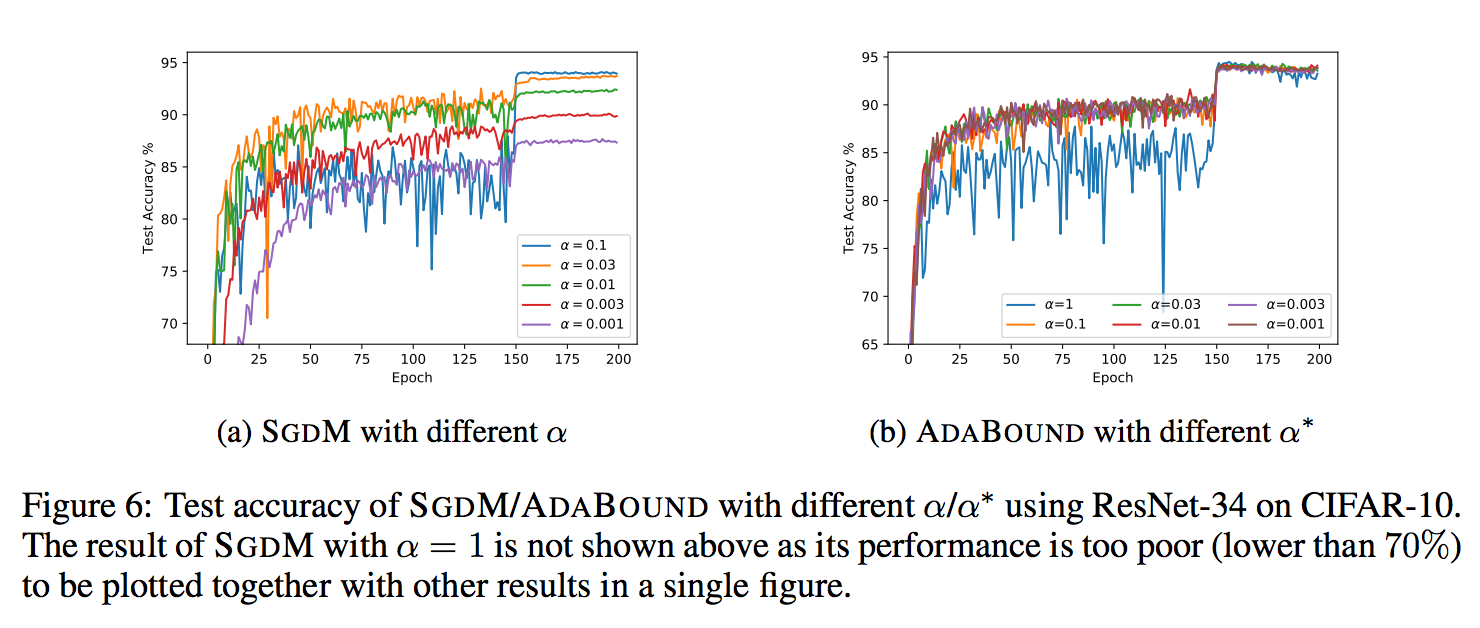
SGDMは学習率$\alpha$の値によって、大きく精度が変わるが
AdaBoundは最終学習率$\alpha^*$をいくつにしても高い精度を保っている

#性能比較
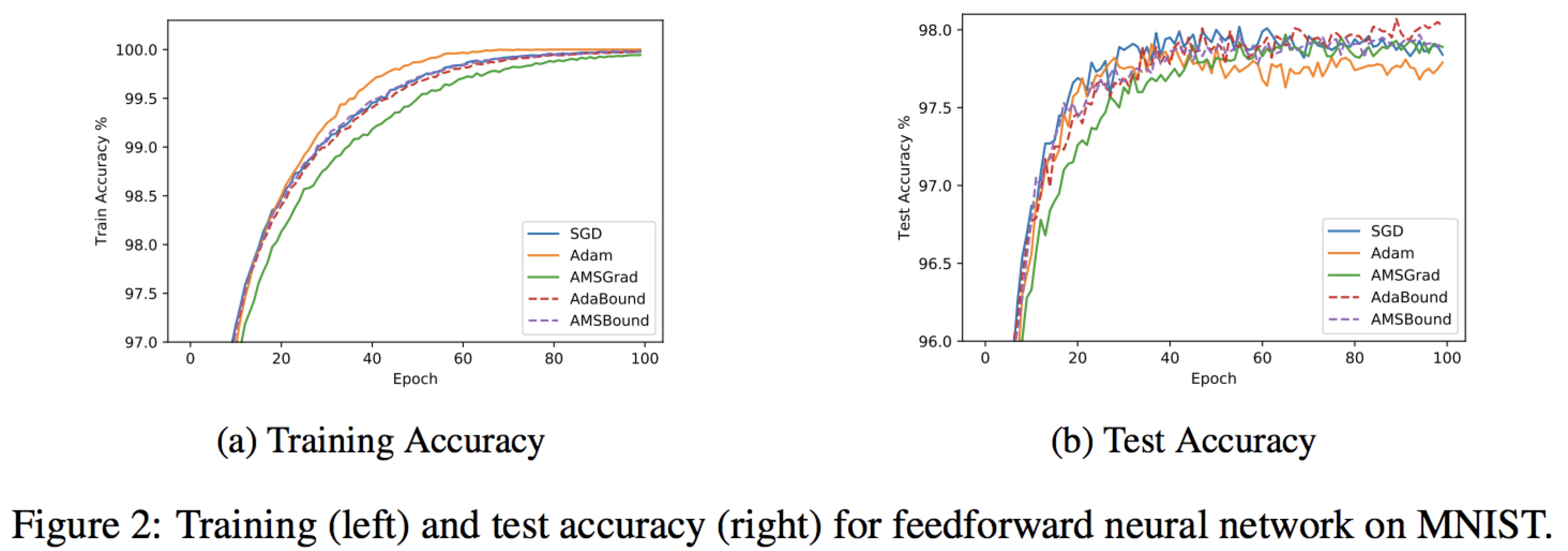
##フィードフォワードニューラルネットワーク

AdaBoundとAMSBoundは改善前（Adam）よりも向上している

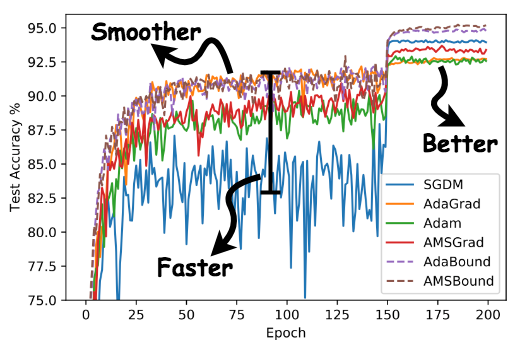
##CNN

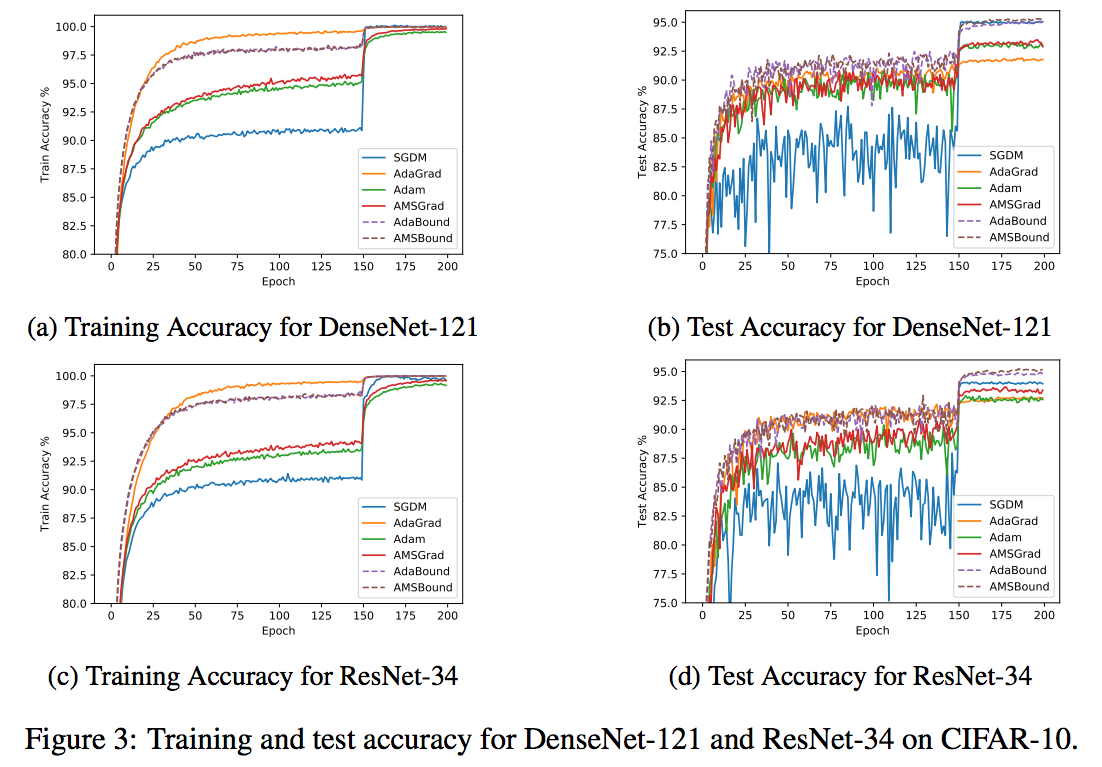
DenseNet・ResNetどちらでも、最初は適応型手法（Adagrad,Adam,AMSgrad）が良いが、後半（150エポックぐらい）になるとSGDの方が良くなる

本研究で提案したAdaBoundとAMSBoundは最初からAdamより良く、後半に入ってもSGDより良い（どの学習段階でも高性能）という結果になった
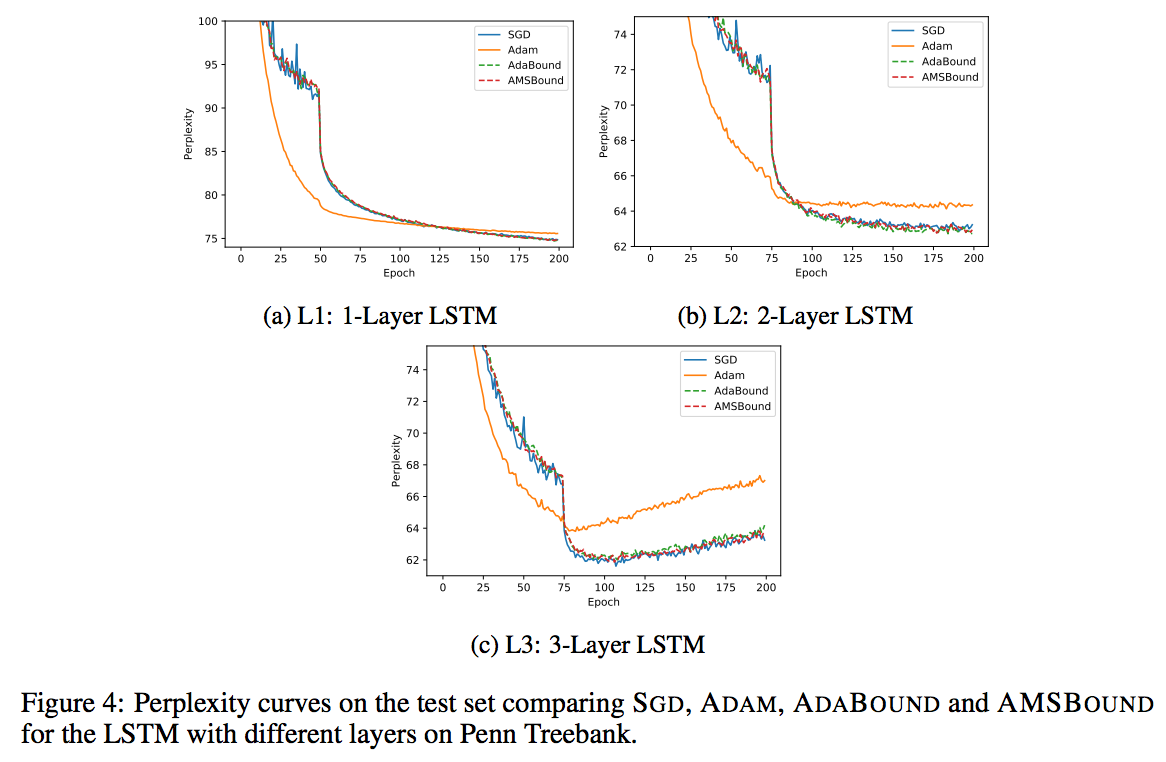
#LSTM

評価指標がPerplexityのため値が小さい方が良い

L1,L2,L3（レイヤーの数）それぞれでAdamとAdaBound・AMSBoundを比較するとモデルが複雑になればなるほどPerplexityが向上していることがわかる

モデルが複雑であるほどAdaBoundとAMSBoundは有効であることがわかる

#まとめ
・学習率の上限と下限を動的に定めるAdaBoundとAMSBoundは
Adamの良さである初期の学習の速さとSGDの良さである汎化能力を両立した最適化手法である

・モデルが複雑になればなるほどAdaBoundとAMSBoundは有効である

・AdaBoundとAMSBoundはハイパーパラメーターの選択に対してロバストである

#関連論文
AMSGradについて
http://www.satyenkale.com/papers/amsgrad.pdf