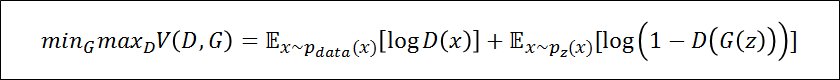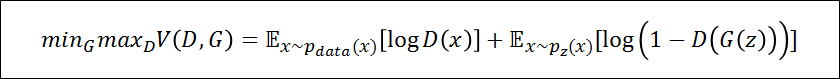GANを学びたいけれど、価値関数の数式に困惑している人へ

#GANの価値関数（目的関数）

本記事ではGANを学び始めたら見かけてしまう、一見複雑そうな上記の式を解説していく

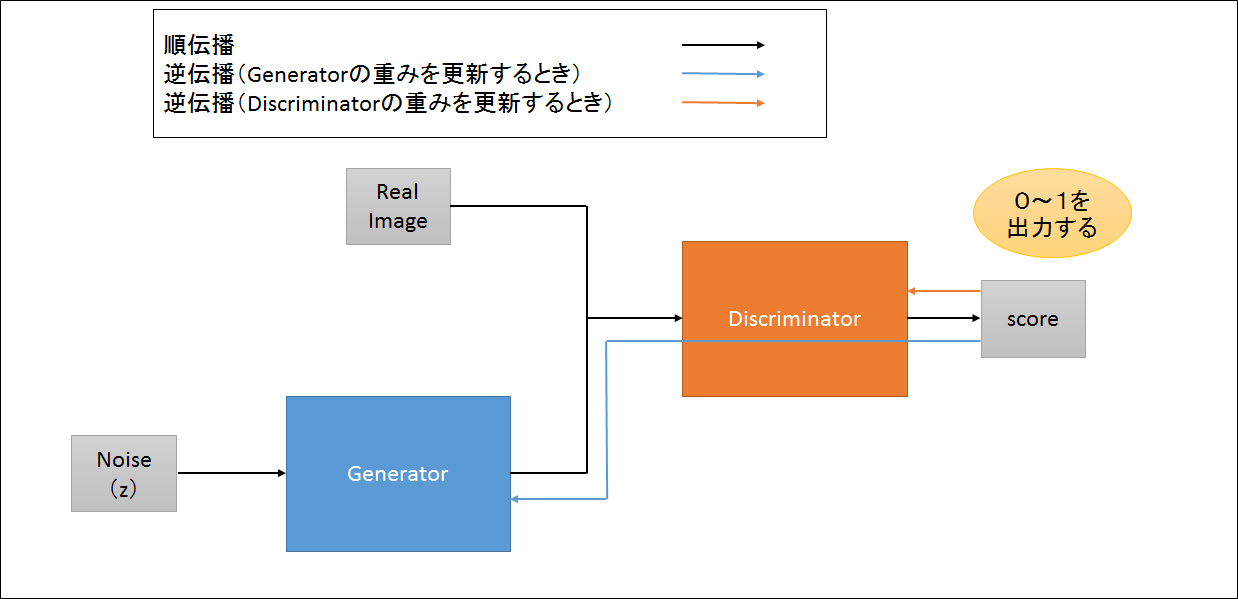
#GANのモデル
まずはGANのモデルと学習の流れを軽く見てみる

##順伝播（Discriminatorに判定させてみる）
・Generatorがノイズ（例えば100次元のベクトル）から画像っぽいものを生成する
もちろん最初はでたらめな画像しか生成できない

・Discriminatorには本物の画像、もしくはGeneratorが生成した画像のどちらかをランダムに入れる

・Discriminatorがスコアを出すときはシグモイド関数を使うため、
本物だと思ったら1を出力、Generatorが生成した画像(偽物）だと思ったら0を出力する

正確にいうと「Discriminatorに来た画像が本物である確率」

##逆伝播（Discriminatorの重みを更新するとき）
Discriminatorの理想は本物が来たら1を出力して、偽物が来たら0を出力

・ここはシンプルに画像分類をしたときのCNNの重みの更新と同じ
GANだからと言って新しい何かがあるわけではない
正しく判定（本物が来たら1を出力して、偽物が来たら0を出力）できるように重みを更新する

##逆伝播（Generatorの重みを更新するとき）
Generatorの理想はDiscriminatorが間違って判定（偽物の画像に対して1を出力）すること

・これは実装上のポイントにもなるが
Generatorの重みを更新するときは、誤差がDiscriminatorを通ってくるため
Discriminatorの重みの更新を止めなければならない

もしDiscriminatorの重みの更新を止めなかったら、Discriminatorの重みが偽物に対して1を出力するようになってしまう（今はGeneratorの理想に近づくような更新がされているため）

#本題へ
GANの価値関数（再掲）

###右辺について###

$E$：期待値
$x$~$p_{data}(x) $：本物の画像がDiscriminatorに来たとき
$D(x)$：Discriminatorに本物の画像が来たときのスコア

$x$~$p_z(x)$：Generatorが生成した画像（偽物）がDiscriminatorに来たとき
$G(z)$：Generatorがノイズzから生成した偽物画像
$D(G(z))$：Discriminatorに（Generatorが生成した）偽物の画像が来たときのスコア

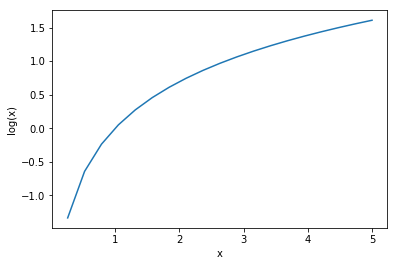
###logのグラフ
log(x)のxの値が大きいほどlog(x)は大きくなる

#Discriminatorを評価するとき
・Discriminatorの理想は本物が来たら1、偽物が来たら0を出力すること
##右辺第一項

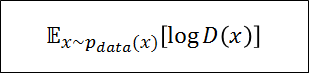
上記の式を言語化すると、本物の画像がDiscriminatorに来たときのDiscriminatorのスコアである

本物の画像のため、シグモイド関数の出力は０～１の内、１を出力してほしい

理想的な出力である$D(x)=1$を出力できれば、結果的に上記の式（右辺第一項）を最大化できる

##右辺第二項

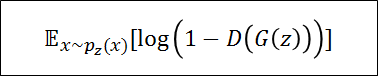
上記の式を言語化すると
Generatorが生成した画像（偽物）がDiscriminatorに来たときのDiscriminatorのスコアである

偽物の画像のため、シグモイド関数の出力は０～１の内、０を出力してほしい

理想的な出力である$D(G(z)))=0$を出力できれば、$log(1-0)$になり
結果的に上記の式（右辺第二項）を最大化できる

##Discriminatorまとめ
上述のようにDiscriminatorの理想通り（本物の画像には1を出力、偽物の画像には0を出力）になれば、
第一項と第二項はどちらも最大になる（大きい値と大きい値を足し合わせているので右辺トータルも最大）

このことを表しているのが、価値関数の左辺にある$max_D$である

#Generatorを評価するとき
・Generatorの理想はDiscriminatorが間違って判定（偽物の画像に対して1を出力）すること

・右辺第一項はGeneratorに関係ないので無視する
##右辺第一項

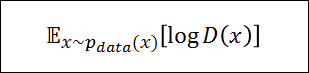
本物の画像がDiscriminatorに来たときのDiscriminatorのスコアを表している

これはGeneratorとは関係がないのでGeneratorを評価するときは無視する

##右辺第二項

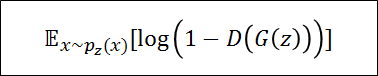
Generatorが生成した画像（偽物）がDiscriminatorに来たときのDiscriminatorのスコアを表している

GeneratorはDiscriminatorが間違ってほしい
Generatorにとっては、偽物画像に対してDiscriminatorが1を出力するのが理想

理想的な出力である$D(G(z))=1$を出力できれば、$log(1-1)$になり
結果的に右辺第二項を最小化できる

##Generatorまとめ
上述のようにGeneratorの理想通り（Generatorの生成した画像に対してDiscriminatorが1を出力）になれば、第二項は最小になる（第一項は無視、第二項最小化で右辺トータルは最小）

このことを表しているのが、価値関数の左辺にある$min_G$である

#全体まとめ
文字が多くて圧倒されてしまいがちな式だが、
「GeneratorとDiscriminatorのそれぞれの理想の状況ってどうなんだっけ？」と落ち着いて考えていけば、「そんな複雑なことを表している式ではないんだな」ということが理解できると思う