Qiitaで電子回路の記事書いていいの?
Qiitaは、プログラマのための技術情報共有サービスです。 プログラミングに関するTips、ノウハウ、メモを簡単に記録 & 公開することができます。
任意の「入力があって出力があるような函」を作るのであれば今回の電子回路の設計も一つのプログラミングといえるのではと思い恐る恐る.
あとすでに電子回路のタグがあったのでいいのではないかなと.
電気回路と電子回路の違い
電気回路はRCL等受動素子のみ,電子回路はRCLまたはそれ以外(能動素子)を含むものらしい.へえ.
Background
できるだけ部品小さめの電流制御回路を作りたかった
Abstract
入力電圧によって電流出力を制御する回路のうちオペアンプをもちいたもので
他に能動素子を使わず出力型にするための工夫をした回路の解説.
電圧電流変換回路
(準備)オペアンプを用いた非反転増幅回路による電圧制御
(準備)片側が接地した抵抗にかかる電圧を一定にして定電流にする
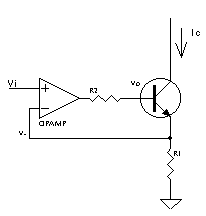

なひたふさんより.
トランジスタのない(出力電流もオペアンプのから持ってくるような)さらに概念的なの探したけど無かった.
一定値の抵抗$R_l$に既知の電圧$V_i$をかければそこに一定の電流$I_o$が流れるので,これに負荷を直列につなげばよい.
抵抗の精度が良くて,抵抗にかける電圧を精度よく一定にできれば,電流もきっと精度良い.
抵抗が発熱しなきゃもっといいかもしれない
ただし,この場合負荷を電圧電源とFET(トランジスタ,あるいは負帰還の点)との間に置くような構成(吸い込み型)となっている.
(本命)抵抗の両端に係る電圧を一定にして定電流にする
さっきの基本構成を吐き出し型にするには
- カレントミラー回路を増設する
- ハイサイド型にする
など他にも方法はあるが今回は抵抗両端の電位差を作ることで実現したもの.
さっきは電流を作る抵抗の一端を接地していたが,今回はその端もフィードバックに加えることで電位差を作る.
すなわち以下の図で,$V_s = (V_1 - V_2) = A\cdot V_{in} (A \in \mathbb{R}) ... (\star)$であればうれしい.
結論から言うと$\frac{R_2}{R_1}=\frac{R_4}{R_3}$でかつ$I_p << I_{out}$となるようにすればよい.以下解説:
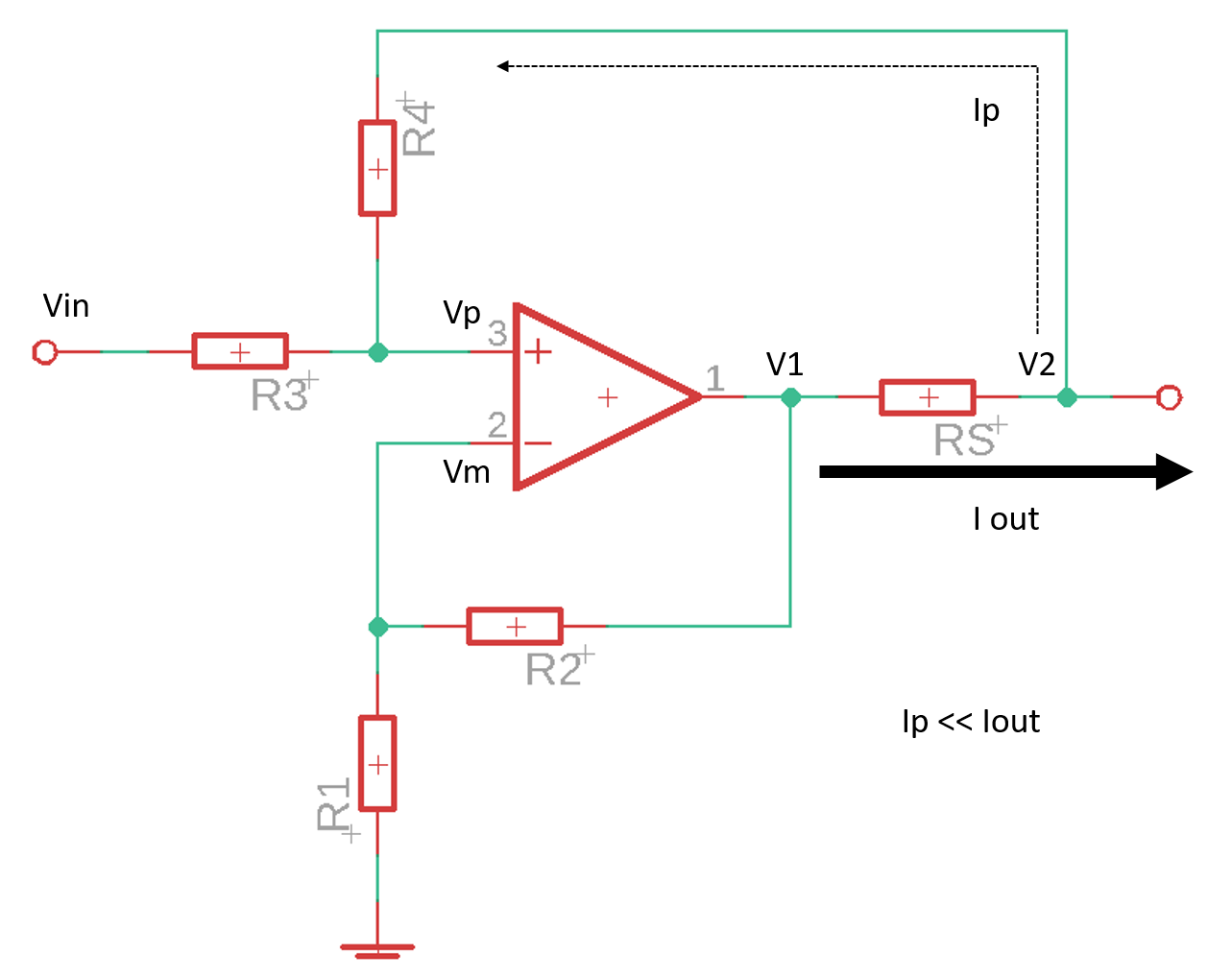
今,$V_1$は入力が$V_p$であるような非反転増幅回路の出力だから,バーチャルショートからすぐに
$$
V_1 = \frac{R_1+R_2}{R_1}V_p
$$
またオペアンプの入力抵抗が超でかいので,$R_{n}>0$の下で,$V_p$と同電位の点についてキルヒホッフの電流測から
$$
\frac{V_2-V_p}{R_4}=\frac{V_p-V_{in}}{R_3}$$ $$
\Leftrightarrow
V_p=\frac{R_3 \cdot V_2 + R_4 \cdot V_{in}}{R_3+R_4}
$$
さっきの式の$V_p$に代入して
$$
V_1 = \frac{R_1+R_2}{R_1} \cdot \frac{R_3 \cdot V_2 + R_4 \cdot V_{in}}{R_3+R_4}$$$$
\Leftrightarrow
V_1-kV_2 = k\frac{R_4}{R_3}V_{in}\ \ \ \ \left( k:=\frac{R_3(R_1+R_2)}{R_1(R_3+R_4)} \right)
$$
$k$が1になってくれればこの式は$(\star)$となり,
$$
(k=)\frac{R_3(R_1+R_2)}{R_1(R_3+R_4)}=1\
\Leftrightarrow
\frac{R_1}{R_2}=\frac{R_3}{R_4}
$$
となってあの条件式が出てくる.そしてこのとき,
$$V_s = (V_1 - V_2) = \frac{R_2}{R_1} \cdot V_{in}$$
以上から入力電圧が$V_{in}$のとき,抵抗$R_5$に電位差$\frac{R_2}{R_1}V_{in}$が生じて,出力電流$I_o$は
$$
I_o = \frac{R_2}{R_1 \cdot R_5}V_{in}
$$
となって電圧($V_{in}$)を電流($I_o$)に変換できている.
以下はざわざわウエアズさんより.
正帰還っぽい方へ電流流れない方がうれしいので$R_4$の片側ではボルテージフォロアで$V_2$を参照.
$I_p$が超小さくなるような抵抗を選んでR4の右側をR5の右側(V2)に短絡させれば上のトラ技の構成と基本は同じ.

その他
PMOSをハイサイドにおくことによる吐き出し型
トランジスタまたはFETを用いた出力側の分離
