はじめまして
この記事はレイトレアドベントカレンダー2021の記事として作成されました。
初めてレイトレアドベントカレンダーを書かせていただきます。質問や間違いがありましたらコメントにてお願いします。
動機
Stan Zurek, CC BY-SA 3.0 http://creativecommons.org/licenses/by-sa/3.0/, via Wikimedia Commons
上図の様な色収差をレイトレーシングで計算したいなと思い、本記事でリアルなカメラレンズをシミュレーションしました。
概要
光の周波数を考慮できるようにレンダリング方程式を拡張し、ガラスでの屈折率を周波数に依存させたりと他にも周波数に依存する物理現象を計算可能にします。おまけとして、計算の効率化についても解説します。
レンダリング方程式
$$L_0(x, \vec{\omega_0}) = L_e(x, \vec{\omega_0}) + \int_{S^2} f_s(x, \vec{\omega_i}, \vec{\omega_0} ) L_i(x, \vec{\omega_i}) |\vec{\omega_i} \cdot \vec{n}| d\vec{\omega_i})$$
この有名なレンダリング方程式に、光の周波数を考慮させるようにします。
$$L_0(x, \vec{\omega_0}, \lambda) = L_e(x, \vec{\omega_0}, \lambda) + \int_{S^2} f_s(x, \vec{\omega_i}, \vec{\omega_0}, \lambda) L_i(x, \vec{\omega_i}, \lambda) |\vec{\omega_i} \cdot \vec{n}| d\vec{\omega_i})$$
ただ、周波数$\lambda$引数を追加しただけです。
これで特定の周波数の輝度が分かるようになります。
| レンダリング方程式 | 光の周波数を考慮されたレンダリング方程式 | |
|---|---|---|
| 入力 | $x, \omega_o$ | $x, \omega_o, \lambda$ |
| 出力 | 輝度(RGB) | 特定の周波数の輝度 |
スペクトルから色情報に変換
周波数を考慮しないレンダリング方程式は計算結果をそのままRGBとして扱えますが、周波数を考慮した方程式は任意の周波数輝度スペクトラムをRGBに変換する必要があります。ここでスペクトラムからRGBに変換について説明します。
しかし、スペクトラムから直接RGBに変換すると被積分式が負の値を持つことがあるので少し複雑になってしまいます。なので、スペクトラムからXYZに一旦変換した後にRGBに変換します。これによって非負な被積分式を扱うことができます。
下の式でスペクトラムからXYZに変換できます。$P(\lambda)$はスペクトラム、$vis$は可視光域、$\bar{x}(\lambda),\bar{y}(\lambda),\bar{z}(\lambda)$はxyzの等色関数です。等色関数の近似式はWikiページを参照
$$y = \int_{vis} \bar{y}(\lambda) d\lambda$$
$$X = \frac{1}{y} \int_{vis} P(\lambda) \cdot \bar{x}(\lambda) d\lambda$$
$$Y = \frac{1}{y} \int_{vis} P(\lambda) \cdot \bar{y}(\lambda) d\lambda$$
$$Z = \frac{1}{y} \int_{vis} P(\lambda) \cdot \bar{z}(\lambda) d\lambda$$
次に積分結果のXYZをRGBに変換します。この変換式はディスプレイのRGB色空間によって変わるので気を付ける必要があります。
sRGB(D65)の場合の変換式は以下です。
\begin{bmatrix}
R \\
G \\
B
\end{bmatrix}
=
\begin{bmatrix}
3.2410 & -1.5374 & -0.4986 \\
-0.9692 & 1.8760 & 0.0416 \\
0.0556 & -0.2040 & 1.0507
\end{bmatrix}
\begin{bmatrix}
X \\
Y \\
Z
\end{bmatrix}
他の色空間ヘの変換はこのサイトが参考になります。
これで周波数を考慮したレンダリング方程式の計算結果をRGBを得る事ができるようになりました。
導出
前の章で計算の流れは分かったと思いますが、実際にプログラムに書くには$L_0(x, \vec{\omega_0}, \lambda)$の具体的な式が未定なので定積分で解くことはできません。よってモンテカルロ法を用いて数値計算で解きます。
$$X(x, \vec{\omega_0}) = \frac{1}{y} \int_{vis} L_0(x, \vec{\omega_0}, \lambda) \cdot \bar{x}(\lambda) d\lambda$$
一様に可視光の領域をサンプルするようなモンテカルロ法を実行します。
まず、一様なPDFを準備します。$C$は定数です。
$$p(\lambda) := C$$
定義域内で積分して1にならないといけないので、
$$\int_{vis} p(\lambda) d\lambda = 1$$
$$\int_{vis} C d\lambda = 1$$
$$C = \frac{1}{\int_{vis} d\lambda}$$
$vis \in [380, 780]$より
$$C = \frac{1}{400}$$
$$p(\lambda) = \frac{1}{400}$$
$p(\lambda)$のCDF$P(\lambda)$ は
$$P(\lambda) = \int_{380}^\lambda \frac{1}{400} d\lambda'$$
$$= \frac{\lambda - 380}{400}$$
逆関数法より
$\xi_\lambda$は[0, 1)範囲の一様乱数
$$P^{-1}(\xi_\lambda) = 400\xi_\lambda + 380$$
$$X(x, \vec{\omega_0}) = \frac{1}{y} \int_{vis} \frac{L_0(x, \vec{\omega_0}, \lambda) \cdot \bar{x}(\lambda)}{p(\lambda)} p(\lambda) d\lambda$$
モンテカルロ法を用いて
$$X(x, \vec{\omega_0}) \approx \frac{1}{y} \frac{1}{N} \sum_{i=1}^N \frac{L_0(x, \vec{\omega_0}, \lambda_i) \cdot \bar{x}(\lambda_i)}{p(\lambda_i)} $$
$$X(x, \vec{\omega_0}) \approx \frac{1}{y} \frac{400}{N} \sum_{i=1}^N L_0(x, \vec{\omega_0}, \lambda_i) \cdot \bar{x}(\lambda_i) $$
これで数値計算でXの期待値を得る事ができ、Y,Zも同様にします。
$$Y(x, \vec{\omega_0}) \approx \frac{1}{y} \frac{400}{N} \sum_{i=1}^N L_0(x, \vec{\omega_0}, \lambda_i) \cdot \bar{y}(\lambda_i) $$
$$Z(x, \vec{\omega_0}) \approx \frac{1}{y} \frac{400}{N} \sum_{i=1}^N L_0(x, \vec{\omega_0}, \lambda_i) \cdot \bar{z}(\lambda_i) $$
プログラム
struct Vec3{
double x,y,z;
};
Vec3 xbybzbFromWavelength(double lambda) {
Vec3 xyz;
xyz.x = 1.056*gausse(lambda, 599.8, 37.9, 31.0) + 0.362*gausse(lambda, 442.0, 16.0, 26.7) - 0.065*gausse(lambda, 501.1, 20.4, 26.2);
xyz.y = 0.821*gausse(lambda, 568.8, 46.9, 40.5) + 0.286*gausse(lambda, 530.9, 16.3, 31.1);
xyz.z = 1.217*gausse(lambda, 437.0, 11.8, 36.0) + 0.681*gausse(lambda, 459.0, 26.0, 13.8);
return xyz;
}
Vec3 SpectrumPathTracing(Vec3 point, Vec3 direction) {
double integral_y = 106.91973463815504343620398716858; // =int_{vis} \bar{y}(\lambda) d\lambda
Vec3 spectrumRadiance;
for (int s=0;s<samples;++s) {
double wavelength = sampleXYZ();
Vec3 xyz = xbybzbFromWavelength(wavelength);
double incomingRadiance = PathTracing(wavelength);
spectrumRadiance.x += incomingRadiance * 400 * xyz.x / integral_y / samples ;
spectrumRadiance.y += incomingRadiance * 400 * xyz.y / integral_y / samples;
spectrumRadiance.x += incomingRadiance * 400 * xyz.z / integral_y / samples ;
}
return spectrumRadiance;
}
結果
 |
|---|
| 通常レンダリング |
 |
|---|
| スペクトルレンダリング |
| 上図は、周波数依存で屈折率が変わるガラスオブジェクト、カメラレンズでスペクトルレンダリングした結果です。 |
| スペクトルのサンプル数 | パストレーシングのサンプル数 | スーパーサンプリング |
|---|---|---|
| 200 | 100 | 4 |
 |
 |
|---|---|
| スペクトルレンダリング | 通常レンダリング |
上図では、白色のライトを拡大した画像です。スペクトルレンダリングでは白ライトの青い周波数帯が屈折のずれで外側にずれてることが分かります。
 |
 |
|---|---|
| スペクトルレンダリング | 通常レンダリング |
| 上図では、ガラスオブジェクトを拡大した画像です。ここでも色収差が確認できます。 |
インポータンスサンプリング
前の章でモンテカルロ法を用いてXYZの期待値を求めることができるようになりました。しかし、完全ランダムで任意の周波数をサンプルするよりも等色関数$\bar{x},\bar{y},\bar{z}$に従ってサンプルした方が収束が早くなります。
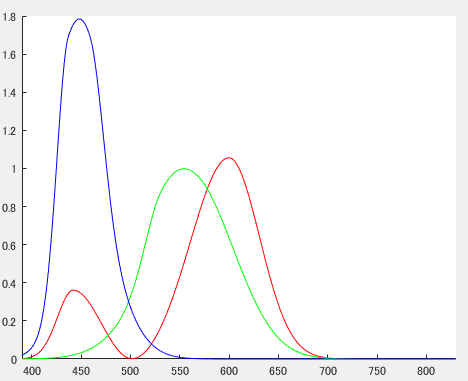
上の図は等色関数$\bar{x},\bar{y},\bar{z}$です。
例えば、610nmと700nmでのサンプルはXYZの期待値の影響具合が違います。影響具合が大きい周波数を優先してサンプルすると収束が早くなります。この方法をインポータンスサンプリングと言います。
適切なPDF
適切なPDF用意して分散がより小さい式を採用します。
$X,Y,Z$に対して適切なPDFかを評価してみます。
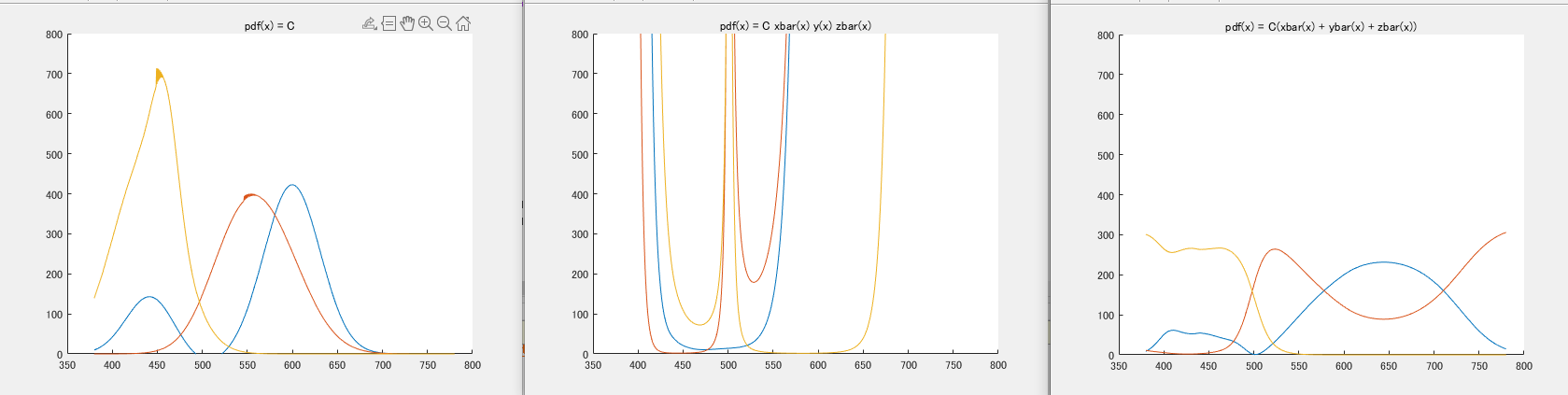
$p_1(\lambda) \propto 1$
$p_2(\lambda) \propto \bar{x}(\lambda) \bar{y}(\lambda) \bar{z}(\lambda)$
$p_3(\lambda) \propto \bar{x}(\lambda) + \bar{y}(\lambda) + \bar{z}(\lambda)$
上は比較するPDFになります。
(これよりもっと分散が小さくできるPDFがあるかもしれませんので探してみるのもいいかもしれません。)
$$X_{mean} = \int_{vis} \bar{x}(\lambda) d\lambda$$
$$Var(X)^2 = \int_{vis} (\lambda-X_{mean})^2 \bar{x}(\lambda) d\lambda$$
$$= \int_{vis} (\lambda-X_{mean})^2 \frac{\bar{x}(\lambda)}{p(\lambda)} p(\lambda) d\lambda$$
$P(\lambda) = \int_{380}^{\lambda} p(\lambda') d\lambda'$
$P$はCDFです。
$\lambda_i = P^{-1}(\xi) = 400 \xi + 380$
$\xi$は[0, 1)の一様乱数として、サンプル点$\lambda_i$を得ることができます。
$$Var(X)^2 = \frac{1}{N} \sum_i^N (\lambda_i-X_{mean})^2 \frac{\bar{x}(\lambda_i)}{p(\lambda_i)}$$
上の式より各$X$の分散を算出します。$Y,Z$も同様にします。
| Xの分散 | Yの分散 | Zの分散 | |
|---|---|---|---|
| $p_1(\lambda)$ | 132.264193 | 139.578475 | 211.571531 |
| $p_2(\lambda)$ | 61817.248718 | 23832.438535 | 144.585084 |
| $p_3(\lambda)$ | 73.824666 | 87.238794 | 124.222135 |
| ※N = 1e7 の実行結果です。 |
数値、図から分かるように$p_3(\lambda)$が一番分散が小さいので、この式を使います。
乱数生成
今回は棄却法を使ってサンプル点を生成する関数を使います。
棄却法は複雑な式などでも扱えます。今回扱う$\bar{x}, \bar{y} \bar{z}$のような解析的に解くことが難しい式に対しても適応することができます。
デメリットとしては、次元が増えるとサンプル点1つを出すのに計算時間がかかる事があるので気を付けましょう。次元の呪いと言うようですね。今回は入力変数が1つで良かったのですが、2つ,3つ,...となると棄却法から別な方法に変える事を考える必要があるかもしれません。
double GenerateSamplePoint() {
// f関数に沿ったサンプル点を考える
while(true) {
xi_x = x_min + (x_max-x_min)*rand();
xi_y = y_max*rand();
if (xi_y < f(xi_x)) {
return xi_x;
}
}
}
等色関数に沿ったサンプル点を求めることができたので、次はモンテカルロ法を用いたインポータンスサンプリングを行います。
導出
レイトレーシングした計算結果を$X, Y, Z$で使いまわすので、$X,Y,Z$それぞれに対して分散を小さくしてあげる必要があります。
等色関数のPDFを用意します。
PDFを$\bar{x}(\lambda) + \bar{y}(\lambda) + \bar{z}(\lambda)$に比例するように定義する。
$$p(\lambda) := C (\bar{x}(\lambda) + \bar{y}(\lambda) + \bar{z}(\lambda))$$
PDFより積分して1になるように$C$を求める
$$\int_{vis} p(\lambda) d\lambda = 1$$
$$\int_{vis} C (\bar{x}(\lambda) + \bar{y}(\lambda) + \bar{z}(\lambda)) d\lambda = 1$$
$$C = \frac{1}{ \int_{vis} \bar{x}(\lambda) + \bar{y}(\lambda) + \bar{z}(\lambda) d\lambda }$$
定数$C$を数値計算で出しておきます。
$$\frac{1}{C} = \int_{vis} \bar{x}(\lambda) + \bar{y}(\lambda) + \bar{z}(\lambda) d\lambda$$
$$p(\lambda) := \frac{1}{400}$$
$\xi_{\lambda}$は[0, 1)の一様な乱数とします。
$$\lambda_i = P^{-1}(\xi_{\lambda}) = 400 \xi_{\lambda} + 380$$
$$\frac{1}{C} = \int_{vis} \frac{\bar{x}(\lambda) + \bar{y}(\lambda) + \bar{z}(\lambda) }{p(\lambda)} p(\lambda) d\lambda$$
モンテカルロ法を用いて
$$\frac{1}{C} \approx \frac{1}{N} \sum_{i=1}^{N} \frac{\bar{x}(\lambda) + \bar{y}(\lambda) + \bar{z}(\lambda) }{p(\lambda)} $$
$$= \frac{400}{N} \sum_{i=1}^{N} ( \bar{x}(\lambda) + \bar{y}(\lambda) + \bar{z}(\lambda) )$$
レンダリングする前に計算してプログラムに定数として書いておきます。($C$は定数なので、レンダリングする際に毎回計算する必要はありません。)
$\lambda_i := GenerateSamplePoint()$
$$X(x, \vec{\omega_0}) = \frac{1}{y} \int_{vis} \frac{L_0(x, \vec{\omega_0}, \lambda_i) \cdot \bar{x}(\lambda)}{p(\lambda)} p(\lambda) d\lambda$$
モンテカルロ法を用いて
$$X(x, \vec{\omega_0}) \approx \frac{1}{y} \frac{1}{N} \sum_{i=1}^N \frac{L_0(x, \vec{\omega_0}, \lambda_i) \cdot \bar{x}(\lambda_i)}{p(\lambda_i)} $$
$$ = \frac{1}{y} \frac{1}{N} \sum_{i=1}^N \frac{L_0(x, \vec{\omega_0}, \lambda_i) \cdot \bar{x}(\lambda)}{ C(\bar{x}(\lambda) + \bar{y}(\lambda) + \bar{z}(\lambda)) } $$
$$ = \frac{1}{y N C} \sum_{i=1}^N \frac{L_0(x, \vec{\omega_0}, \lambda_i) }{ 1 + \frac{\bar{y}(\lambda)}{\bar{x}(\lambda)} + \frac{\bar{z}(\lambda)}{\bar{x}(\lambda)} } $$
同様に他の$Y,Z$導出する。
$$Y(x, \vec{\omega_0}) \approx \frac{1}{y N C} \sum_{i=1}^N \frac{L_0(x, \vec{\omega_0}, \lambda_i) }{ \frac{\bar{x}(\lambda)}{\bar{y}(\lambda)} + 1 + \frac{\bar{z}(\lambda)}{\bar{y}(\lambda)} } $$
$$Z(x, \vec{\omega_0}) \approx \frac{1}{y N C} \sum_{i=1}^N \frac{L_0(x, \vec{\omega_0}, \lambda_i) }{ \frac{\bar{x}(\lambda)}{\bar{z}(\lambda)} + \frac{\bar{y}(\lambda)}{\bar{z}(\lambda)} + 1 } $$
プログラム
struct Vec3{
double x,y,z;
};
Vec3 xbybzbFromWavelength(double lambda) {
Vec3 xyz;
xyz.x = 1.056*gausse(lambda, 599.8, 37.9, 31.0) + 0.362*gausse(lambda, 442.0, 16.0, 26.7) - 0.065*gausse(lambda, 501.1, 20.4, 26.2);
xyz.y = 0.821*gausse(lambda, 568.8, 46.9, 40.5) + 0.286*gausse(lambda, 530.9, 16.3, 31.1);
xyz.z = 1.217*gausse(lambda, 437.0, 11.8, 36.0) + 0.681*gausse(lambda, 459.0, 26.0, 13.8);
return xyz;
}
double sampleXYZ() {
while (true) {
double xi_x = (color::MAX_WAVELENGTH - color::MIN_WAVELENGTH) * rand.RandomGenerate() + color::MIN_WAVELENGTH;
auto max = 2.1655154441358; // max value of x+y+z
double xi_y = rand() * max;
auto point = color::xbybzbFromWavelength(xi_x);
double y = point.x + point.y + point.z;
if (xi_y < y) {
return xi_x;
}
}
}
Vec3 SpectrumPathTracing(Vec3 point, Vec3 direction) {
double integral_xyz = (106.76504616237932261548607350578+106.91973463815504343620398716858+106.82532490175775630470443615231); // =int_{vis} \bar{x}(\lambda) \bar{y}(\lambda) + \bar{z}(\lambda) d\lambda
double integral_y = 106.91973463815504343620398716858; // =int_{vis} \bar{y}(\lambda) d\lambda
Vec3 spectrumRadiance;
for (int s=0;s<samples;++s) {
double wavelength = sampleXYZ();
Vec3 xyz = xbybzbFromWavelength(wavelength);
double incomingRadiance = PathTracing(wavelength);
spectrumRadiance.x += incomingRadiance / (1.0 + xyz.y/xyz.x + xyz.z/xyz.x) / integral_y * integral_xyz / samples ;
spectrumRadiance.y += incomingRadiance / (xyz.x/xyz.y + 1.0 + xyz.z/xyz.x) / integral_y * integral_xyz / samples;
spectrumRadiance.x += incomingRadiance / (xyz.x/xyz.z + xyz.y/xyz.z + 1.0) / integral_y * integral_xyz / samples ;
}
return spectrumRadiance;
}
評価
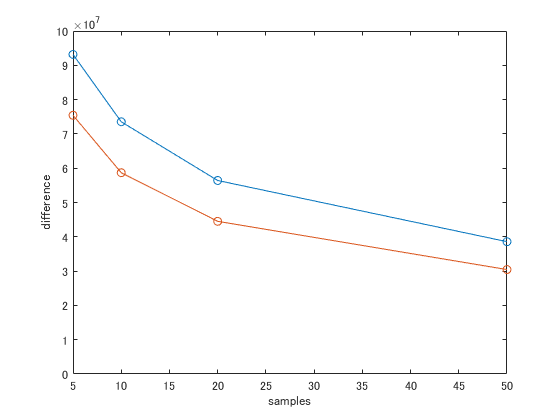
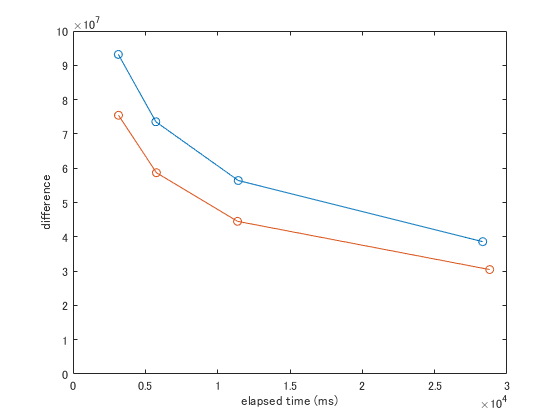
完全なランダムサンプルとインポータンスサンプリングの2つの手法でのレンダリングと十分にサンプルしたリファレンス画像との比較します。青線は完全なランダムサンプル、赤線はインポータンスサンプリングです。
上図は横軸は計算時間、縦軸は差分です。
レンダリング結果
| スペクトルサンプル数 | パストレーシングのサンプル数 |
|---|---|
| 5 | 25 |
図と画像からインポータンスサンプリングの方が収束が早いことが分かります。インポータンスサンプリングは棄却法の影響で1サンプルの計算時間が少しかかることが分かりますが、それ以上に収束に早めることができています。
git
参考文献
大田登『色彩工学』、東京電機大学出版局、2001年
まとめ
一様乱数を使ったスペクトルレンダリングまではそんなに大変ではなかったのですが、インポータンスサンプリングが少し厄介でした。等色関数が複雑な式で構成されているので逆関数法ができず色々悩んでいました。そこで、初めて棄却法をレンダリングに取り入れたのですが、とても分かりやすくシンプルで強力な手法だと思いました。棄却法はちゃんと短所もあり、棄却法と逆関数法は両極端ですね。
今後
今回はガラスの屈折具合をあり得ないくらい分散させたので、次は現実的な屈折ができるようにCauchy's equationを使いたいと思います。
今回のカメラレンズは単純な凸レンズ(虫眼鏡)でレンダリングしたので、カメラレンズの構成についてもやってみたいなと思います。
色々やることが多そうですが、色収差はとても綺麗ですね!(^▽^)
(最近、デノイザーとか面白そうだなーと浮気をしそうです。)