More than 1 year has passed since last update.

Juliaで常微分方程式を解く

Last updated at 2022-06-26Posted at 2021-03-14

Juliaで力学系の計算コードを書いていたところ、日本語記事が少なかったためメモ

ローレンツ方程式

ローレンツ方程式は熱対流の流れを単純化した方程式であり、次の式で表される。
ここではTsit5 (Tsitouras 5/4 Runge-Kutta法) を用いてこの方程式を解く。

\begin{eqnarray}
  \left\{
    \begin{array}{l}
      \frac{dx}{dt} &=& -px+py \\
      \frac{dy}{dt} &=& -xz+rx-y \\
      \frac{dz}{dt} &=& xy-bz
    \end{array}
  \right. \nonumber
\end{eqnarray}

常微分方程式の定義

マクロ@ode_defを使用し、常微分方程式を定義する。
このマクロでは、左辺のdで始まる変数は自動的に時間微分されているものと解釈され、その他のパラメータ変数(p,r,b) はendの後に記述する。
また、時間変数は暗黙にtと定義される。

using ParameterizedFunctions, DifferentialEquations
using Plots
using CPUTime

# 常微分方程式の定義
g = @ode_def LorenzExample begin
    dx = p*(y-x)
    dy = x*(r-z) - y
    dz = x*y - b*z
  end p r b

問題定義

続いて、常微分方程式の問題を定義する。
ODEProblemコンストラクタに先ほどの常微分方程式gとx,y,zの初期値u0、タイムスパンtspan、パラメータpを与えてインスタンス化する。

u0 = [0.0;1.01;0.0]
tspan = (0.0,100.0)
p = [10.0,25.0,7/3]
prob = ODEProblem(g,u0,tspan,p)

計算

solve()で実際に問題を解く。数値解法はnon-stiffな（数値不安定でない）方程式の解法に推奨されていたTsit5を使用した。
マクロ@CPUTimeで実行時間を計測できる。（elapsed CPU time: x.xx secondsのようにコンソールに出力される）

@CPUtime sol = solve(prob,Tsit5(),reltol=1e-8,abstol=1e-8)

描画

描画はパッケージPlotsを使用し、静止画とgifの両方を出力した。（gifの作成には時間がかかるので注意）

計算結果

lorenz.jl

using ParameterizedFunctions, DifferentialEquations
using Plots
using CPUTime

# 常微分方程式の定義
g = @ode_def Lorenz begin
    dx = p*(y-x)
    dy = x*(r-z) - y
    dz = x*y - b*z
  end p r b

# 問題定義
u0 = [0.0;1.01;0.0]
tspan = (0.0,100.0)
p = [10.0,25.0,7/3]
prob = ODEProblem(g,u0,tspan,p)

# 計算
@CPUtime sol = solve(prob,Tsit5(),reltol=1e-8,abstol=1e-8)

function plt()
    plot(sol,vars=(1,2,3), title="Lorenz Attractor", 
        xlabel="x", ylabel="y", zlabel="z", label="")
    savefig("lorenz.png")
end

function pltgif()
    plt = plot3d(1, xlim=(-20,20), ylim=(-20,25), zlim=(0,40),
                title = "Lorenz Attractor", 
                xlabel="x", ylabel="y", zlabel="z",
                size=(640, 480),
                label="")
    anim = @animate for step in 1:size(sol)[2]
        push!(plt, sol[1,step], sol[2,step], sol[3,step])
    end every 10
    gif(anim, "lorenz.gif", fps=30)
end

# 描画
@CPUtime plt()
@CPUtime pltgif() #時間がかかるので注意

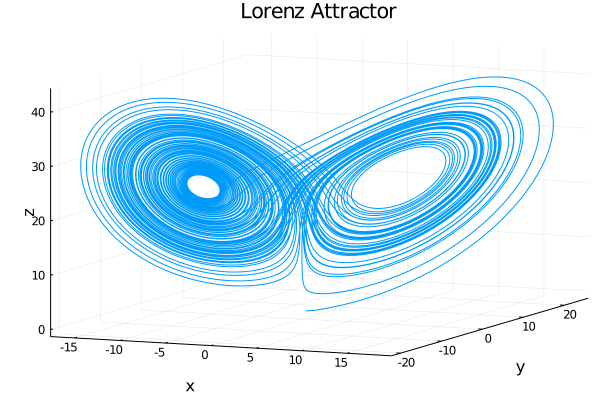
上記のコードを実行すると、以下のようにローレンツアトラクタを出力できる。
因みに実行時間は以下の通りで、gifの描画に時間がかかる。
Juliaの実行はVSCode上でShift + Enterで実行すると実用上楽で速い。（> julia 〇〇.jl してはいけないよ[実行方法]）
・計算時間：elapsed CPU time: 2.328 seconds
・静止画描画時間：elapsed CPU time: 1.484 seconds
・gif描画時間：elapsed CPU time: 143.782 seconds

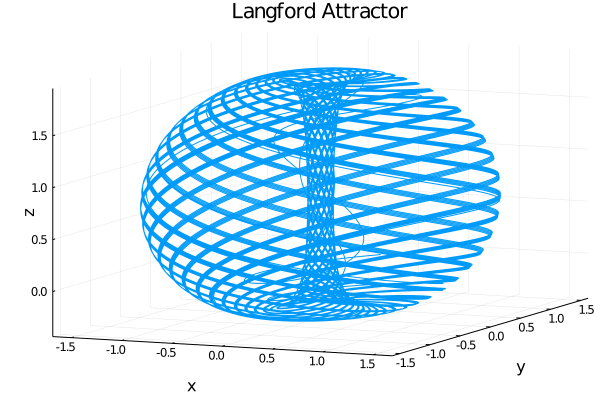
ラングフォード方程式

以下のラングフォード方程式についても、常微分方程式と問題の定義を変更することで同様に容易に解くことができる。

\begin{eqnarray}
  \left\{
    \begin{array}{l}
      \frac{dx}{dt} = (z-u)x-wy \\
      \frac{dy}{dt} = wx-(z-u)y \\
      \frac{dz}{dt} = n+z-\frac{z^3}{3}-(x^2+y^2)(1+lz)+ezx^3
    \end{array}
  \right. \nonumber
\end{eqnarray}

langford.jl

using ParameterizedFunctions, DifferentialEquations
using Plots
using CPUTime

# 常微分方程式の定義
g = @ode_def Langford begin
    dx = (z-u)*x - w*y
    dy = w*x + (z-u)*y
    dz = n + z - (z^3)/3.0 - (x^2+y^2)*(1+l*z)
  end u w n l

# 問題定義
u0 = [0;1;0]
tspan = (0,500)
p = [0.7,3.5,0.6,0.25]
prob = ODEProblem(g,u0,tspan,p)

# 計算
@CPUtime sol = solve(prob,Tsit5(),reltol=1e-8,abstol=1e-8)

function plt()
    plot(sol,vars=(1,2,3), title="Langford Attractor", 
        xlabel="x", ylabel="y", zlabel="z", label="")
    savefig("langford.png")
end

function pltgif()
    plt = plot3d(1, xlim=(-1.5,1.5), ylim=(-1.5,1.5), zlim=(-0.5,2),
                title = "Langford Attractor", 
                xlabel="x", ylabel="y", zlabel="z",
                size=(640, 480),
                label="")
    anim = @animate for step in 1:size(sol)[2]
        push!(plt, sol[1,step], sol[2,step], sol[3,step])
    end every 10
    gif(anim, "langford.gif", fps=30)
end

# 描画
@CPUtime plt()
@CPUtime pltgif() #時間がかかるので注意

参考文献

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up