【Python】Pokémon UNITEの勝率のモデリングを通して確率・統計の雰囲気をつかむ

はじめに

【Python】専門書や論文を読みたいけど数学が苦手・わからない人向けのコードを読んで学ぶ数学教本の番外編です(第2弾の記事は下書きは終わっていますのでしばしお待ちを)。この記事では現実の問題をモデル化して考える材料を作るというデータサイエンスっぽい事をやっていきます。タイトル通り『Pokémon UNITE』における勝率のモデル化というのがメインの話になりますので、遊んだことがない人はインストールして数十回遊んでからこの記事に戻ってきて下さい。この記事はポケモンユナイトの勝率に関する研究で、数式やプログラムを組み上げるの{を見守る・に参加する}というものになります。そのため、知識を得たい人には合わない内容かと思います。最終的な結果等は別記事に作りますので、洗練されたまとまった知識を学びたい場合はそちらをお読み下さい。拙文ですが、内容が面白いと思ったらお勧めしてくれたらうれしいです。徐々に更新してく予定ですのでストック等お願いします。

ソースコード(MITライセンス)：(https://github.com/PHVTuber/WinningPercentageSimulation-PokemonUNITE.git)

用語の整理

ここでは以降の議論で使う用語とその意味を軽くまとめておきます。

略称	意味	補足
オブジェクト	ロトム、カジリガメ、サンダーなどの大型野生ポケモン	-
ソロ	チームを組まない	-
デュオ	2人でチームを組む	-
トリオ	3人でチームを組む	-
スクワッド	4人でチームを組む	-
フルパ	5人でチームを組む	-
バックドア(BD)	相手のスキをついてゴールを決める	ユナイトではサンダー戦中にゴールを決める事を『サンダー戦時のBD』ではなく、単にBDと呼ぶ事が多い
キャリー	ダメージを出すキャラ(アタック、スピード、バランス型とか)。または、勝利に導いた人	文脈によって意味が変わりますが、この記事では基本的に後者の意味で使います
BDマン	サンダー戦時にBDするプレイヤー	-

勝率について

『Pokémon UNITE』は5 vs. 5に分かれてゴールを決め、最終的な得点を競うというゲームです。5人でチームを組むという性質上、そのゲームの勝敗はチームメイトに依存する事になります。しかし、要所要所での活躍(LHの精度、指示能力、求心力など)を再現性を持って行えるような人であれば、チームメイトの質には依存するものの試合を勝利に傾ける事が出来るため、勝利：

勝率 [\%] = \frac{勝利回数}{試合数}

が高くなりやすいと言えるかと思います。こよれり、上手さと勝率は比例すると言えるかもしれません。しかし、このゲームではフレンドとパーティングを組んでランクマッチに参加できるため、勝率の解釈を複雑化させます。デュオやトリオでランクマッチに潜るとなると、ソロの勝率が高い人の勝率に引きずられやすいため、勝率と上手さが1対1対応しないプレイヤーが出てくると考えられる訳ですね。以降は断りがない限り、ソロを前提のモデルを構築していきます。

検証1

検証内容

上手さの具体的な形はおいおい考えるとして、まずはこの上手さが等価な人のみで試合を$100,500,1000$とさせたとき、勝率の分布はどうなるのか? また、勝率が近い人とマッチしてるっぽいシステムが有効に働いているのか? という点はどうなっているのだろうか。

また、この問い上手さが等価のケースを考えている事から、試合結果が$1/2$という運にのみ左右されたケースを考えている事と等価と言えるかと思います。

検証1のための前準備

アカウント作成

Playerの情報を管理するクラスを作成します。まずは簡単に勝率を保持したクラスを作っていきます。ここらも後ほど複雑化していきます。

from decimal import Decimal, ROUND_HALF_UP
import random

class Player:
    """
    アカウントの各属性値を保持

    Attributes
    --------------
    name : str
        アカウント名(ID)
    num_games : int
        試合数
    wins : int
        勝利数
    wp : float
        勝率(winning percentage) (=勝利数/試合数)
    rank : str
        ランク {beginner,super,hyper,elite,exper,master}
    """
    def __init__(self,name,rank="master"):
        """
        Parameters
        -------------------
        name : str
            アカウント名
        rank : str
            {beginner,super,hyper,elite,exper,master}
        """
        self.name = name
        self.rank = rank
        self.num_games = 0
        self.wins = 0
        self.wp = 0.

    def status(self):
        # ステータス
        print(f"user name:{self.name},\n rank:{self.rank},\n number of games:{self.num_games},\n winning percentage:{self.wp}[%]")

    def result_win(self):
        # 勝利時の処理
        self.num_games += 1
        self.wins += 1
        wp = self.wins/self.num_games*100 # 勝率
        wp = Decimal(str(wp)).quantize(Decimal('0.1'),rounding=ROUND_HALF_UP) # 小数第一位まで
        self.win_rate = float(wp)

    def result_loss(self):
        # 敗北時の処理
        self.num_games += 1
        wp = self.wins/self.num_games*100
        wp = Decimal(str(wp)).quantize(Decimal('0.1'),rounding=ROUND_HALF_UP)
        self.wp = float(wp)

    def rank_up(self):
        # ランクアップ
        ranks = ["beginner","super","hyper","elite","exper","master"]
        if self.rank == "master":
            # 元からmasterなら何もしない
            pass
        else:
            idx = ranks.index(self.rank) # ranks内から該当のrankを検索
            self.rank = rank[idx+1] # 自身のrankの上のrankに書き換える

    def reset(self):
        # アカウントのステータスをリセット
        self.rank = rank
        self.num_games = 0
        self.wins = 0
        self.wp = 0.

試合内容

決着がランダムに決まるとは、コインを振って表か裏かで試合結果を決めるようなものなので、random.uniform(0.0,1.0)で乱数を生成して0.5を超えるか超えないか考えるだけで良い訳ですね。

def match_time_1(team1,team2):
    """
    決着は運によってのみ決まる場合
    """
    # 完全なランダム
    p = random.uniform(0.0,1.0)
    if p>=0.5:
        # team1が勝利、tema2が敗北
        for teammate1,teammate2 in zip(team1,team2):
            teammate1.result_win()
            teammate2.result_loss()
    else:
        # team1が敗北、tema2が処理
        for teammate1,teammate2 in zip(team1,team2):
            teammate1.result_loss()
            teammate2.result_win()

マッチングシステム

ここでは2つのマッチングシステムを作ってみます。

• 無作為に$5$人と$5$人を選ぶ(matching_system_1関数)
• 勝率が近い人で$10$人選んで$5$対$5$を作る(matching_system_2関数)

現在、勝率が近い人と組ぬようなシステムになっているようですが、選出方法が不明なのでぽい感じのシステムを用意します。$10$人分の勝率をまとめたリスト$List_{o}$を昇順に直したリストを$List_u =\sigma (List_{o})$とします。このリストから$team_{1}$と$team_{2}$に下記のように振り分けます。

team_{1} = [List_{u} [0],List_{u} [3],List_{u} [4],List_{u} [7],List_{u} [8]]\\
team_{2} = [List_{u} [1],List_{u} [2],List_{u} [5],List_{u} [6],List_{u} [9]]

def matching_system_1(players_matching):
    """
    無作為にチームを組む

    Returns
    -------------
    pairs : マッチングしたチームとチームを1つにまとめたリストを試合が成立した数だけ保持したリスト
        　　リストを作る.
            e.g.) pairs = [[team1,team2],[team3,team4],...]
                  これは team1 vs. team2, team3 vs.team4, ...を意味する
    """
    num_events = len(players_matching)//10 # 行われる試合数
    players_matching_success = random.sample(players_matching,k=num_events*10)
    players_shuffle = players_matching_success.copy()
    random.shuffle(players_matching_success) # ランダムに並び替え
    # players_matching_success を5人チームごとに分ける
    players_shuffle = [players_shuffle[idx:idx+5] for idx in range(0,len(players_shuffle),5)]

    # eventごとにまとめる
    pairs = []
    for i in range(0,len(players_matching_success),2):
        pairs.append([[players_matching_success[i]],[players_matching_success[i+1]]])
    return pairs

def matching_system_2(players_matching):
    """
    勝率の近い人でマッチング

    Returns
    -------------
    pairs : マッチングしたチームとチームを1つにまとめたリストを試合が成立した数だけ保持したリスト
        　　リストを作る.
            e.g.) pairs = [[team1,team2],[team3,team4],...]
                  これは team1 vs. team2, team3 vs.team4, ...を意味する
    """
    num_events = len(players_matching)//10 # 行われる試合数
    players_matching_success = random.sample(players_matching,k=num_events*10)
    players_sort = players_matching_success.copy()
    # 昇順に並び替える
    players_sort.sort(key=lambda x:x.wp)
    # players_sort を10人ごとに分ける
    players_sort = [players_sort[idx:idx+10] for idx in range(0,len(players_sort),10)]

    # eventごとにまとめる
    pairs = []
    for players in players_sort:
        team1 = [players[0],players[3],players[4],players[7],players[8]]
        team2 = [players[1],players[2],players[5],players[6],players[9]]
        pairs.append([team1,team2])
    return pairs

図示

ヒストグラムで結果を出力する。binsはお好みで。

def create_histogram(win_rates,num_games):
    fig = plt.figure(figsize=(3.14,3.14))
    ax = fig.add_subplot(111)
    ax.hist(win_rates,bins='auto')
    ax.set_title(f'Number of games: {num_games}')
    ax.set_xlabel("winnig percentage[%]")
    ax.set_ylabel("freq")
    ax.text(0.99,0.99,
            f"max:{max(win_rates)}[%],min:{min(win_rates)}[%]",
            va='top',ha='right',transform=ax.transAxes)
    plt.savefig("winnig_rate_{}.png".format(num_games))

検証1の結果

この検証で使うパラメータは下記にまとめました。

N = 10000 # 競技人口
num_iters = [100,500,1000] # ループ回数
matching_system = matching_system_1 # マッチングシステム {matching_system_1,matching_system_2}
match_time = match_time_1 # 勝敗の要因 {match_time_1}

下記で各試合数におけるヒストグラムを入手していきます。

# アカウント作成
players = []
for i in range(1,N+1):
    players.append(Player(f"{i}"))

# シミュレーション
for num_games in num_iters:
    for i in range(num_games):
        pairs = matching_system(players) # マッチング
        for pair in pairs:
            match_time(*pair) # 試合開始
        win_rates = [player.wp for player in players]
    create_histogram(win_rates,num_games) # 図示
    [player.reset() for player in players] # 初期化

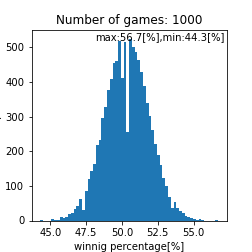
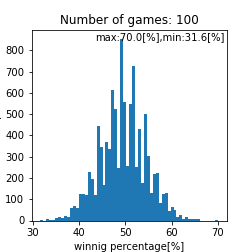
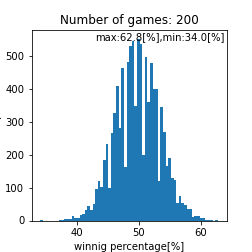
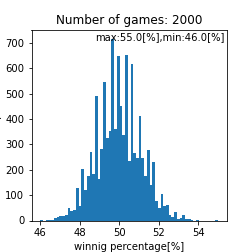
matching_system_1における勝率分布

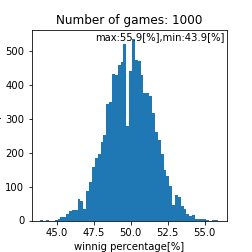
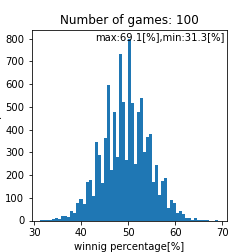
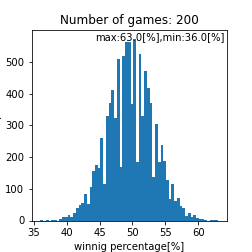
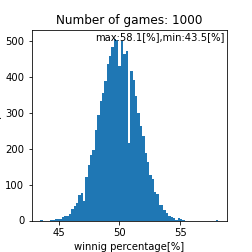
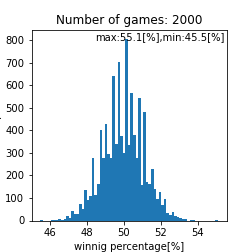
matching_system_2における勝率分布

まとめ

このプログラム内で乱数を使っているのでシミュレーションを数千回から数万回回して再現性を確認をするのですがこれは個々人で確認してもらうとして、ここら辺で一旦まとめておきます。試合回数をこなしていくと勝率は$50[\%]$に収束する事しそうですね(確率論において重要なポイント)。ただし、$1000$回程度の試合数だと、まだ勝率は収束せず$44.0-56.0[\%]$あたりに勝率が収まるという事がわかります。ただ、$1000$回以上試合をソロでこなしており、勝率が$56[\%]$を超えているのであれば、その人は間違いなくキャリーであると言えるでしょう。また、$44[\%]$以下なら敗因は自分にあると言えるかかもしれません。実際の分布として比較して、その分布と似ていればこのモデルで説明できているという事になりますね(統計学において重要なポイント)。

検証2 - 救済措置

検証内容

連敗すると発生するCPU戦の効果は勝率分布にどのような影響を及ぼしているのか? CPU戦は連敗が続くと、救済措置として発生するイベントです。何連敗で発生するのかはランク帯に依存するらしく、マスター戦では$5$連敗すると発生するCPU戦が発生するらしいです(要検証)。極端な話、CPU戦だけにしか勝てないのであれば勝率は$100/6\approx 17[\%]$であるため、十数回以上を試合をこなしているのであれば勝率が$1$桁の人はいないはず。。!

検証2の前準備

アカウント作成

連敗状況を保持する関数をPlayerクラスに追加します(setattr等を使った方がわかりが良かったですかね?)。

class Player:
    """
    アカウントの各属性値を保持

    Attributes
    --------------
    name : str
        アカウント名(ID)
    num_games : int
        試合数
    wins : int
        勝利数
    wp : float
        勝率(winning percentage) (=勝利数/試合数)
    rank : str
        ランク {beginner,super,hyper,elite,exper,master}
    loss_cnt : int
        連敗数
    cpu_cnt : int
        cpu戦突入回数
    """
    def __init__(self,name,rank="master"):
        """
        Parameters
        -------------------
        name : str
            アカウント名
        rank : str
            {beginner,super,hyper,elite,exper,master}
        """
        self.name = name
        self.rank = rank
        self.num_games = 0
        self.wins = 0
        self.wp = 0.
        self.loss_cnt = 0
        self.cpu_cnt = 0

    def status(self):
        # status
        print(f"user name:{self.name},\n rank:{self.rank},\n number of games:{self.num_games},\n winning percentage:{self.wp}[%]")

    def result_win(self):
        # 勝利時の処理
        self.num_games += 1
        self.wins += 1
        self.loss_cnt = 0 # 連敗リセット
        wp = self.wins/self.num_games*100 # 勝率
        wp = Decimal(str(wp)).quantize(Decimal('0.1'),rounding=ROUND_HALF_UP) # 小数第一位まで
        self.win_rate = float(wp)

    def result_loss(self):
        # 敗北時の処理
        self.num_games += 1
        self.loss_cnt += 1
        wp = self.wins/self.num_games*100
        wp = Decimal(str(wp)).quantize(Decimal('0.1'),rounding=ROUND_HALF_UP)
        self.wp = float(wp)

    def rank_up(self):
        # ランクアップ
        ranks = ["beginner","super","hyper","elite","exper","master"]
        if self.rank == "master":
            # 元からmasterなら何もしない
            pass
        else:
            idx = ranks.index(self.rank) # ranks内から該当のrankを検索
            self.rank = rank[idx+1] # 自身のrankの上のrankに書き換える

    def cpu_counter(self):
        self.cpu_cnt += 1

    def reset(self):
        # アカウントのステータスをリセット
        self.num_games = 0
        self.wins = 0
        self.wp = 0.
        self.loss_cnt = 0
        self.cpu_cnt = 0

連敗マッチング

ランクによってCPU戦までに必要な連敗数が異なるのでその点を加味したい所だが、ネットくに詳しい情報がないので$5$連敗でCPU戦突入とします(詳しい情報求む)。

def matching_system_loss(players):
    """
    連敗数を調査し、一定数を超えていたら、cpu戦させる.

    Returns:
    ---------------------
    players_pvp : list
        cpu戦の必要がない人のリスト
    """
    # CPU戦になるplayerのリスト
    players_cpu = list(filter(lambda x:x.loss_cnt>=5,players))

    # CPU戦には必ず勝つ
    for player in players_cpu:
        player.result_win()
        player.cpu_counter()

    # PvP戦に参加する人のリスト
    players_pvp = list(set(players)-set(players_cpu))
    return players_pvp

検証2の結果

# parameters
N = 10000 # 競技人口
num_iters = [1000] # ループ回数
matching_system = matching_system_2 # マッチングシステム
match_time = match_time_1 # 勝敗の要因

# アカウント作成
players = []
for i in range(1,N+1):
    players.append(Player(f"{i}"))

# シミュレーション
for num_games in num_iters:
    for i in range(num_games):
        players_pvp = matching_system_loss(players)
        pairs = matching_system(players_pvp) # マッチング
        for pair in pairs:
            match_time(*pair) # 試合開始
        win_rates = [player.wp for player in players]
    create_histogram(win_rates,num_games) # 図示
    [player.reset() for player in players] # 初期化

まとめ

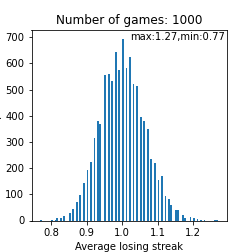
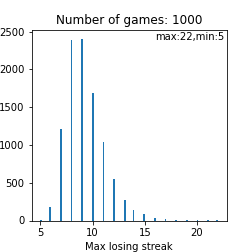
検証1で触れたようにシミュレーション回数を増やさないと詳しくはわかりませんが、検証1の結果を比較すると、分布を右にシフトさせるような効果がありそうですね。下図は救済措置なしの場合の平均連敗記録と連敗の最大値の分布です。

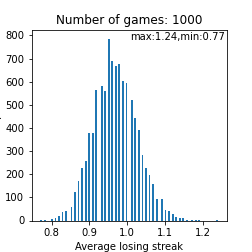
人によっては20連敗程度もあり得るという事ですね。恐ろしい。。。下図は救済措置ありのときの平均連敗数と最大連敗数の分布です。救済措置ありなしで平均構造に大きな変化は見られなさそうですが、救済措置5連敗以上起こらない訳なのでかなりの人の下振れが阻止されている事は推測できます。つまり、恩恵を受けてる人は多く存在する事は言えそうですね。ちなみに上図の2つ目の図はポアソン分布に似ている気がしますが、何か関係はあるのでしょうか? 確認してみて下さい。

検証3 - サンダー戦時のBD

検証内容

このゲームではサンダー戦の勝敗がそのままゲームの勝敗に直結します。序盤から優位をどれだけとれていたとしても、サンダー戦で敗北すれば多くの場合負けてしまいます。サンダー戦で起こる集団戦は人数とユナイト技保持率がものをいうため、人数差がある場合は基本的には不利です。それなのに、一定数BDに行ってしまう人がいるのがこのゲームです。もちろん、BDが有効に働く場面もない訳ではないですが、大抵負けます(体感9割)。という事でBDする人が多いチームは必ず負けるというモデルにおける勝率の分布はどうなるのでしょうか?

検証内容の分析

このゲームでは得点数が高いほど、計算上チームの貢献度が高いと判断されます。サンダー戦時の得点は$2$倍になるため、BDが成功すると$100$点入る計算になります。現時点(2022/1/30)ではセカンドゴールを攻める事が少し難しいので、サンダー戦開始時点の得点は上下のファーストゴール$160/5=32$点あたりが1人あたりの得点数の期待値となります。その後、サンダー戦に勝てば$100$点が上乗せされる訳なので、その人の勝率を$p_{i}$と置けば、平均得点数$G_{i}$は

G_{i} = 32 + 100p_{i}

程度を取る事になります。例えば、勝率が$50[\%]$であれば$G=32+100\times 0.5=82$と算出できます。加速装置持ちファイアロー、カイリューやイワパレス、ヨクバリスならセカンドゴールまで手が届きやすいので、セカンドゴールへの得点数の期待値を$25$点とすれば

G_{i} = 57 + 100p_{i}

で求められるかもしれません。このとき、勝率が$50[\%]$であれば$G=57+100\times 0.5=107$と算出できます。ダメージを出すキャラという意味でのキャリーであれば、$100p_{i}$ですかね。雑な見積もりなので後ほどこれのモデルも作ってみて分布をみてみましょう。どちらにせよ、勝率に対して予測される期待値より過剰な平均得点を持つ人はBDをしているというのは待ちがないでしょう。こういった人は探せば、結構な割合で存在するのでBDはプレイヤーの属性として考えれば良さそうですね。

検証3の前準備

アカウント作成

Playerクラスの属性にBDを追加して書き換えます。

class Player:
    """
    アカウントの各属性値を保持

    Attributes
    --------------
    name : str
        アカウント名(ID)
    num_games : int
        試合数
    wins : int
        勝利数
    wp : float
        勝率(winning percentage) (=勝利数/試合数)
    rank : str
        ランク {beginner,super,hyper,elite,exper,master}
    loss_cnt : int
        連敗数
    cpu_cnt : int
        cpu戦突入回数
    bd : boolean
        {True:BDする,False:BDしない}
    """
    def __init__(self,name,rank="master"):
        """
        Parameters
        -------------------
        name : str
            アカウント名
        rank : str
            {beginner,super,hyper,elite,exper,master}
        """
        self.name = name
        self.rank = rank
        self.num_games = 0
        self.wins = 0
        self.wp = 0.
        self.loss_cnt = 0
        self.cpu_cnt = 0
        self.loss_cnts = 0
        self.bd = False

    def status(self):
        # status
        print(f"user name:{self.name},\n rank:{self.rank},\n number of games:{self.num_games},\n winning percentage:{self.wp}[%]")

    def result_win(self):
        # 勝利時の処理
        self.num_games += 1
        self.wins += 1
        self.loss_cnt = 0 # 連敗リセット
        wp = self.wins/self.num_games*100 # 勝率
        wp = Decimal(str(wp)).quantize(Decimal('0.1'),rounding=ROUND_HALF_UP) # 小数第一位まで
        self.win_rate = float(wp)

    def result_loss(self):
        # 敗北時の処理
        self.num_games += 1
        self.loss_cnt += 1
        wp = self.wins/self.num_games*100
        wp = Decimal(str(wp)).quantize(Decimal('0.1'),rounding=ROUND_HALF_UP)
        self.wp = float(wp)

    def rank_up(self):
        # ランクアップ
        ranks = ["beginner","super","hyper","elite","exper","master"]
        if self.rank == "master":
            # 元からmasterなら何もしない
            pass
        else:
            idx = ranks.index(self.rank) # ranks内から該当のrankを検索
            self.rank = rank[idx+1] # 自身のrankの上のrankに書き換える

    def cpu_counter(self):
        self.cpu_cnt += 1

    def reset(self):
        # アカウントのステータスをリセット
        self.num_games = 0
        self.wins = 0
        self.wp = 0.
        self.loss_cnt = 0
        self.cpu_cnt = 0
        self.bd = False

　試合内容

BD属性持ちの数を比較後、BD属性持ちが多い方を強制的に負けにし、数が同じであれば関数match_time_1で処理とします。

def match_time_2(team1,team2):
    """
    決着はBDを属性に持ったplayerが多い方が負ける場合.
    BDを属性に持ったplayerが同数の場合はmatch_time_1と同じ処理
    """
    # BDの属性持ちの調査
    num_bd_team1 = [teammate1.bd for teammate1 in team1]
    num_bd_team2 = [teammate2.bd for teammate2 in team2]
    # BDの属性持ち数
    num_bd_1 = num_bd_team1.count(True)
    num_bd_2 = num_bd_team2.count(True)

    if num_bd_1 == num_bd_2:
        # BD
        match_time_1(team1,team2)
    elif num_bd_1<num_bd_2:
        # team2の方がBD属性持ちが多い
        # team1が勝利、tema2が敗北
        for teammate1,teammate2 in zip(team1,team2):
            teammate1.result_win()
            teammate2.result_loss()
    else:
        # team1が敗北、tema2が処理
        for teammate1,teammate2 in zip(team1,team2):
            teammate1.result_loss()
            teammate2.result_win()

BD属性付与

bd_rateでBD属性持ちの全体の割合を制御します。

def assignment_bd(players,bd_rate=0.1):
    """
    クラスPlayerのbdをFalse→Trueに変換
    """
    num_players = len(players)
    players_bd = random.sample(players,k=int(num_players*bd_rate))
    for player in players_bd:
        player.bd = True

図示

def create_histogram(players,num_games,bd_rate):
    win_rates = [player.wp for player in players]
    fig = plt.figure(figsize=(3.5,3.5))
    ax = fig.add_subplot(111)
    ax.hist(win_rates,bins='auto')
    ax.set_title(f'Number of games: {num_games}')
    ax.set_xlabel("winnig percentage[%]")
    ax.set_ylabel("freq")
    ax.text(0.99,0.99,
            f"max:{max(win_rates)}[%],min:{min(win_rates)}[%],bd_rate:{bd_rate*100}[%]",
            va='top',ha='right',transform=ax.transAxes)
    plt.savefig(f"winnig_rate_N{N}_G{num_games}_B{bd_rate}.png")

検証

# parameters
N = 10000 # 競技人口
num_iters = [2000] # ループ回数
matching_system = matching_system_2 # マッチングシステム
match_time = match_time_1 # 勝敗の要因 {match_time_1,match_time_2}
bd_rates = [0.1,0.3,0.5]

# アカウント作成
players = []
for i in range(1,N+1):
    players.append(Player(f"{i}"))

# シミュレーション
for num_games in num_iters:
    for bd_rate in bd_rates:
        assignment_bd(players,bd_rate) # BDマンを生成
        for i in range(num_games):
            players_pvp = matching_system_loss(players) # 救済措置
            pairs = matching_system(players_pvp) # マッチング
            for pair in pairs:
                match_time(*pair) # 試合開始
        create_histogram(players,num_games,bd_rate) # 図示
        [player.reset() for player in players] # 初期化

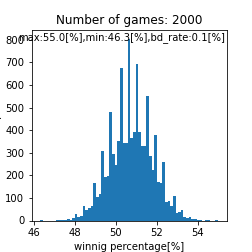
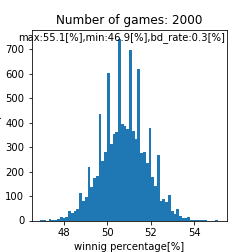
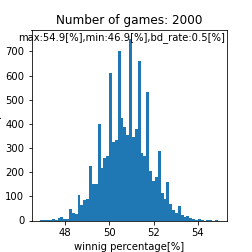
比較対象用として、match_time = match_time_1です。BDがいたとしても運で勝敗が付くケースであり、BD率が異なるものの同じ分布を3回作っているのと同義です。

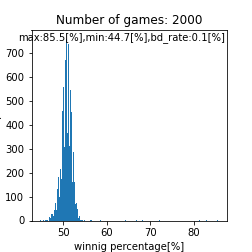
先ほどは特に注目してませんでしたが、救済措置あり運に左右されたケースでは平均が$51[\%]$に移動するみたいですね。下記はmatch_time = match_time_2です。

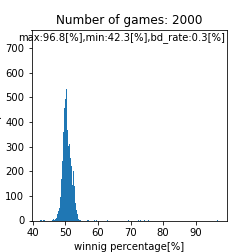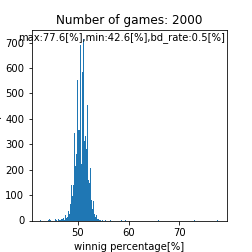正しくはbd_rate=10[%]	正しくはbd_rate=30[%]	正しくはbd_rate=50[%]

• プログラムは修正済み

必ず勝てる試合があれば増える訳なので勝率は高くなりやすいというのは直感通りですね。ただ、面白いのが勝率の最小値が$40[\%]$という点です。このモデルではBDマンが下層に集まる訳ですが、全体に$10[\%]$仲間がいるだけで勝率が$17-40[\%]$の間に入らないというのは驚異ですね。現在のBDマンに反省を促すために、やむを得ずシミュレーションをしたのにこれでは気付くのが難しそうですね。

検証4 - 上手さに差をつける

上手さというものは複数の側面を持つものであるため、少し考えてみます。上手さとはデス率が低い、LHの精度が高い、キル率が高い、味方によるのが早いなどの立ち回りなどを含めた操作的な上手さと1カメ戦敗北後にファームを優先する、カメ戦後に下レーンをがら空きにしないなどの状況判断やファイトよりもゴールを優先するなどの戦略を含めたマクロ的な上手さの2種類があるかと思います。他にも、パーティのバランスを考えてキャラをピックできるなど色々考えられます。考える得る要素を全てリストアップ面倒だし、そもそも、リストアップが可能なのかわからないので、試合の勝利につながりそうな要素の集合を$E$と置きます。この中でミクロに分類できる部分集合を$S$、マクロに分類できる部分集合を$L$とします。ミクロとマクロの間にはメゾというのがあるのですが、この言葉は研究してないとまず耳にしない言葉ですし、このような状態を表すシチュエーションが思いつかいないので$S\cap L$とします。このとき、対象とした人$i$の上手さ$I_{i}$は

I_{i} = c_{S}\sum_{s\in S} w(s) f_{i}(s) + c_{L} \sum_{l\in L} w(l) f_{i}(l)\tag{1}

や

I_i = c_{S}\prod_{s\in S} w(s) f_{i}(s) + c_{L} \prod_{l\in L} w(l) f_{i}(l)\tag{2}

などで表現できるかもしれません。ここで、$c_{S},c_{L}\in [0,1]$はミクロ的な上手さの重み、マクロ的な上手さの重み、$w\in [0,1]$はその要素の重み、$f_{i}$は$E\to \mathbb{R}$という写像を表します。試合を左右するのはミクロ的な上手さとマクロ的な上手さのどちらかが影響として大きいのか? というのを$c_{S},c_{L}$で表現しており、$w$は各要素の上手さどれほど勝利に貢献しやすいのかという事を表しています。式(1)というのは個人の能力を加算方式で評価し、式(2)は1つの要素でも欠ければ無いのと等しいという厳しい評価をするというモデルになります。式(1)、(2)から構築していくというのもありなのですが、ここでは簡単に

I_{i} = c_{S}F_{S,i}+c_{L}F_{L,i}

と考えて、$F_{S,i},F_{L,i}$に対して何かしらの分布を仮定して乱数を入れ込んでしまえば、細かな要素を無視してモデリングできます。$F_{S,i},F_{L,i}$を$[0,10]$とし、$c_{S}+c_{L}=1$と制限してやれば、$I_{i}\in [0,10]$となります。という事で$I_{i}$の分布を考えてやれば良さげですね。また、このとき、検証1はこのモデルの特別な例であり、

I_{1} = I_{2} = \cdots = I_{N} = Const.

を表していた事になります。つまり、検証1の拡張モデルという事ですね。

上手さと勝率は一対一対応していると素直に議論できるのですが、どうなっているのでしょうか? 上手さ毎の分布をプロットして、どこまで反映されるものなのか確認してみましょう。

検証の前準備

アカウント作成

クラスPlayerにstengthという属性を付与します。

class Player:
    """
    アカウントの各属性値を保持

    Attributes
    --------------
    name : str
        アカウント名(ID)
    num_games : int
        試合数
    wins : int
        勝利数
    wp : float
        勝率(winning percentage) (=勝利数/試合数)
    rank : str
        ランク {beginner,super,hyper,elite,exper,master}
    loss_cnt : int
        連敗数
    cpu_cnt : int
        cpu戦突入回数
    bd : boolean
        {True:BDする,False:BDしない}
    strength : int/float
        強さ。strength ∈ [0,10]. 
    """
    def __init__(self,name,rank="master"):
        """
        Parameters
        -------------------
        name : str
            アカウント名
        rank : str
            {beginner,super,hyper,elite,exper,master}
        """
        self.name = name
        self.rank = rank
        self.num_games = 0
        self.wins = 0
        self.wp = 0.
        self.loss_cnt = 0
        self.cpu_cnt = 0
        self.loss_cnts = 0
        self.bd = False
        self.strength = 0

    def status(self):
        # status
        print(f"user name:{self.name},\n rank:{self.rank},\n number of games:{self.num_games},\n winning percentage:{self.wp}[%]")

    def result_win(self):
        # 勝利時の処理
        self.num_games += 1
        self.wins += 1
        self.loss_cnt = 0 # 連敗リセット
        wp = self.wins/self.num_games*100 # 勝率
        wp = Decimal(str(wp)).quantize(Decimal('0.1'),rounding=ROUND_HALF_UP) # 小数第一位まで
        self.win_rate = float(wp)

    def result_loss(self):
        # 敗北時の処理
        self.num_games += 1
        self.loss_cnt += 1
        wp = self.wins/self.num_games*100
        wp = Decimal(str(wp)).quantize(Decimal('0.1'),rounding=ROUND_HALF_UP)
        self.wp = float(wp)

    def rank_up(self):
        # ランクアップ
        ranks = ["beginner","super","hyper","elite","exper","master"]
        if self.rank == "master":
            # 元からmasterなら何もしない
            pass
        else:
            idx = ranks.index(self.rank) # ranks内から該当のrankを検索
            self.rank = rank[idx+1] # 自身のrankの上のrankに書き換える

    def cpu_counter(self):
        self.cpu_cnt += 1

    def reset(self):
        # アカウントのステータスをリセット
        self.num_games = 0
        self.wins = 0
        self.wp = 0.
        self.loss_cnt = 0
        self.cpu_cnt = 0
        self.bd = False
        self.strength = 0

上手さの分布

ここでは簡単に強さの分布が一様に存在するケースと正規分布に従うケースで考えてます。$[0,10]$に数字を分布させる場合、正規分布は使えないため、切断正規分布というものを使います。

def assignment_bd(players,bd_rate=0.1):
    """
    クラスPlayerのbdをFalse→Trueに変換
    """
    num_players = len(players)
    players_bd = random.sample(players,k=int(num_players*bd_rate))
    for player in players_bd:
        player.bd = True

def assignment_strength_uniform(players):
    """
    クラスPlayerのstrengthを一様分布で割り当てる
    """   
    for player in players:
        p = random.uniform(0.0,10.0)
        player.strength = float(Decimal(str(p)).quantize(Decimal('0.1'),rounding=ROUND_HALF_UP)) # 小数第一位まで

def assignment_strength_norm(players,loc=5,scale=2):
    """
    クラスPlayerのstrengthを切断正規分布で割り当てる
    切断正規分布:
    https://en.wikipedia.org/wiki/Truncated_normal_distribution
    """
    bounds = [0,10] # [min=0,max=10]
    for player in players:
        p = turnc_norm(loc,scale,bounds)
        player.strength = float(Decimal(str(p)).quantize(Decimal('0.1'),rounding=ROUND_HALF_UP)) # 小数第一位まで

def turnc_norm(loc,scale,bounds):
    """
    切断正規分布に従う乱数生成

    parameters：
    ----------------------
    loc：int/float
        平均値
    scale：int/float
        標準偏差
    bounds：list
        乱数の最小値と最大値を保持したリスト。[最小値,最大値]
    """
    r = stats.truncnorm.rvs((bounds[0]-loc)/scale, (bounds[1]-loc)/scale, loc=loc, scale=scale)
    return r

試合内容

どんなに圧倒していても、サンダーのLHを取られ、最悪逆転される事を考えると、上手い人が多い人の方が勝つと考えるよりか、勝ちやすいと考える方が現実的でしょう。という事で、チームの強さ$S$を

S(team) = \sum_{teammate\in team} s(teammate)

を定義します。ここで、$s(teammate)$はその上手さを表しています。このとき、$team_1$の勝率$p(team_1)$を

p(team_{1}) = \frac{S(team_{1})}{S(team_{1})+S(team_{2})}

と表現する事にします。ここで、$tema_2$は敵対するチームです。

def match_time_3(team1,team2):
    """
    strengthの総和が高い方が勝ちやすい
    """
    # 総合力
    S1 = sum([teammate1.strength for teammate1 in team1])
    S2 = sum([teammate2.strength for teammate2 in team2])

    # tema1の勝ちやすさ
    p_team1 = S1/(S1+S2)

    # 完全なランダム
    p = random.uniform(0.0,1.0)
    if p <= p_team1:
        # team1が勝利、tema2が敗北
        for teammate1,teammate2 in zip(team1,team2):
            teammate1.result_win()
            teammate2.result_loss()
    else:
        # team1が敗北、tema2が処理
        for teammate1,teammate2 in zip(team1,team2):
            teammate1.result_loss()
            teammate2.result_win()

def match_time_4(team1,team2):
    """
    match_time_2 & match_time_3
    """
    # BDの属性持ちの調査
    num_bd_team1 = [teammate1.bd for teammate1 in team1]
    num_bd_team2 = [teammate2.bd for teammate2 in team2]
    # BDの属性持ち数
    num_bd_1 = num_bd_team1.count(True)
    num_bd_2 = num_bd_team2.count(True)

    if num_bd_1 == num_bd_2:
        # BD
        match_time_3(team1,team2)
    elif num_bd_1<num_bd_2:
        # team2の方がBD属性持ちが多い
        # team1が勝利、tema2が敗北
        for teammate1,teammate2 in zip(team1,team2):
            teammate1.result_win()
            teammate2.result_loss()
    else:
        # team1が敗北、tema2が処理
        for teammate1,teammate2 in zip(team1,team2):
            teammate1.result_loss()
            teammate2.result_win()

図示

def create_histogram(players,num_games,bd_rate,bounds=[0.0,10.0]):
    """
    bounds : list
        図示したいstrengthの範囲。[最小値,最大値]
    """
    players_bound = list(filter(lambda x:(bounds[0]<=x.strength)&(x.strength<=bounds[1]),players))
    win_rates = [player.wp for player in players_bound]
    fig = plt.figure(figsize=(3.5,3.5))
    ax = fig.add_subplot(111)
    ax.hist(win_rates,bins='auto')
    ax.set_title(f'Number of games: {num_games}')
    ax.set_xlabel("winnig percentage[%]")
    ax.set_ylabel("freq")
    ax.text(0.99,0.99,
            f"max:{max(win_rates)}[%],min:{min(win_rates)}[%],bd_rate:{bd_rate}[%]",
            va='top',ha='right',transform=ax.transAxes)
    plt.savefig(f"winnig_rate_N{N}_G{num_games}_B{bd_rate}_bound{bounds[0]}{bounds[1]}.png")

検証

# parameters
N = 10000 # 競技人口
num_iters = [2000] # ループ回数
matching_system = matching_system_2 # マッチングシステム
match_time = match_time_4 # 勝敗の要因
assignment_strength = assignment_strength_uniform # 上手さの分布 {assignment_strength_uniform,assignment_strength_norm}
bd_rates = [0.1,0.3,0.5]

# アカウント作成
players = []
for i in range(1,N+1):
    players.append(Player(f"{i}"))

# シミュレーション
for num_games in num_iters:
    for bd_rate in bd_rates:
        assignment_bd(players,bd_rate) # BDマンを生成
        assignment_strength(players) # 上手さ付与
        for i in range(num_games):
            players_pvp = matching_system_loss(players) # 救済措置
            pairs = matching_system(players_pvp) # マッチング
            for pair in pairs:
                match_time(*pair) # 試合開始
        # 図示
        create_histogram(players,num_games,bd_rate,[0.0,1.0])
        create_histogram(players,num_games,bd_rate,[1.1,2.0])
        create_histogram(players,num_games,bd_rate,[2.1,3.0])
        create_histogram(players,num_games,bd_rate,[3.1,4.0])
        create_histogram(players,num_games,bd_rate,[4.1,5.0])
        create_histogram(players,num_games,bd_rate,[5.1,6.0])
        create_histogram(players,num_games,bd_rate,[6.1,7.0])
        create_histogram(players,num_games,bd_rate,[7.1,8.0])
        create_histogram(players,num_games,bd_rate,[8.1,9.0])
        create_histogram(players,num_games,bd_rate,[9.1,10.0])
        create_histogram(players,num_games,bd_rate,[0.0,10.0])
        [player.reset() for player in players] # 初期化

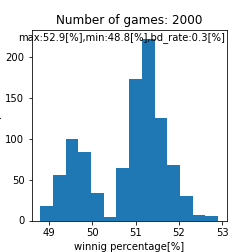
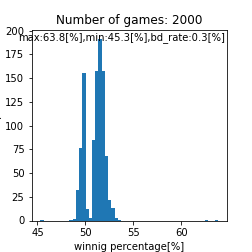
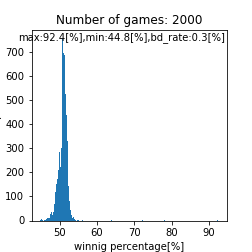
assignment_strength = assignment_strength_uniform

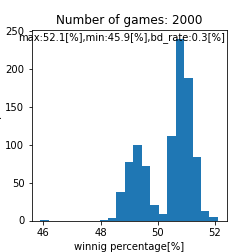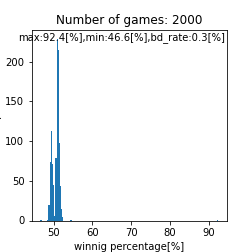bounds=[3.1,4.0]	bounds=[4.1,5.0]	bounds=[5.1,6.0]	bounds=[6.1,7.0]	bounds=[0.0,10.0]

二峰性のグラフが得られるとは。。これは面白い結果が得られましたね。また、上手い人ほど高い勝率を得やすいという点では良さげなモデルが出来ましたね。

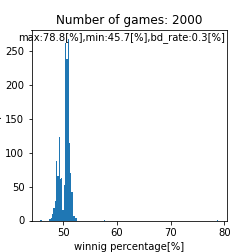
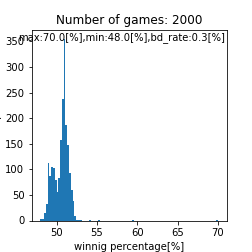
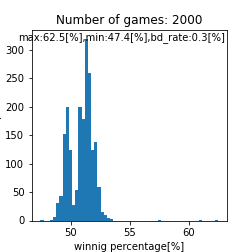
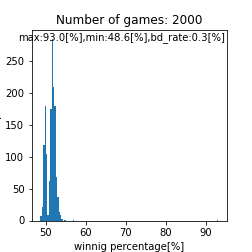
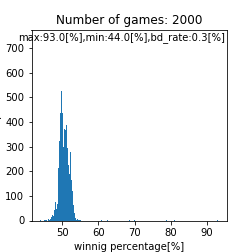
assignment_strength = assignment_strength_norm

bounds=[3.1,4.0]	bounds=[4.1,5.0]	bounds=[5.1,6.0]	bounds=[6.1,7.0]	bounds=[0.0,10.0]

一様分布との違いは1回のデータ生成からは何とも言えませんが、ぱっと見では切断正規分布を仮定すると$50[\%]$弱が最頻値になる感じですかね。平均的な実力を持つ$5-6$が多く存在するモデルであり、この領域のヒストグラムを見てみると$50[\%]$以下の山に入るか$50[\%]$以上の山に入るのか2値なのがわかります。これほど現実に近そうなモデルを作っても$50[\%]$前半の人が$40[\%]$後半の人よりも間違いなく上手いという事を説明できるモデルが用意できないのが残念です。しかし、$55[\%]$以上はランダムの枠を超えているので再現性のある上手さを持っている事は間違いなさそうです。

検証5 - 上手さ成長モデル

検証6 - パーティと上手さの対応関係

検証7 - 良く選ぶキャラと勝率の関係

検証8 - 試合内容のシミュレーション

解析 - データベースから統計データをとってモデルと比較

解析 - 自分の勝率は運なのか