【機械学習】線形回帰 - 直線フィッティング、曲線フィッティング

#はじめに
機械学習を勉強しています。
自分用にまとめます。
数学的に厳密ではないと思います。
理論中心です。
この記事では、「直線フィッティング」と「曲線フィッティング」をやります。
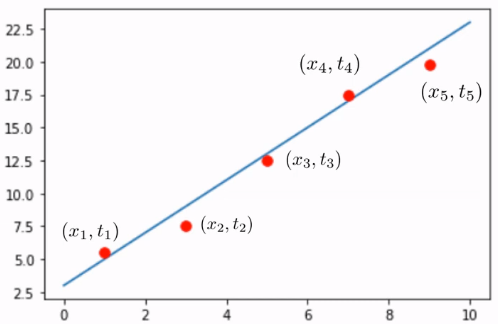
#直線フィッティング
######要件
$N$個のデータ$\{(x_1,t_1),\cdots,(x_N,t_N)\}$に当てはまる直線を求めたい。

######モデルの定義
予測直線(モデル)を$y=w_0+w_1x$とする。
######目的関数の定義
あるデータ$(x_i,t_i)$に着目する。
$x_n$の予測値は$w_0+w_1x_n$である。
$t_n$との差の2乗は$(w_0+w_1x_n-t_n)^2$である。
これを全データについて足し合わせたものを目的関数とする。
$E(w_0,w_1)=\frac{1}{2}\sum_{n=1}^N(w_0+w_1x_n-t_n)^2$
$\frac{1}{2}$は$w_0,w_1$で偏微分した式を奇麗に見せるためのものである。

######目的関数の最小化
目的関数を最小化するために$w_0,w_1$で偏微分し、$=0$とおくと
以下の2式からなる連立方程式ができる。
$\frac{\partial}{\partial w_0}E=\sum_{n=1}^N(w_0+w_1x_n-t_n)=0$
$\frac{\partial}{\partial w_1}E=\sum_{n=1}^Nx_n(w_0+w_1x_n-t_n)=0$
これを解くと$w_0,w_1$が求まり、予測直線が決定する。
(ここでは解かない。直線フィッティングは曲線フィッティングに含まれるため。)

#曲線フィッティング
######要件
要件は「直線フィッティング」の時とほぼ同じ。
$N$個のデータ$\{(x_1,t_1),\cdots,(x_N,t_N)\}$に当てはまる曲線を求めたい。

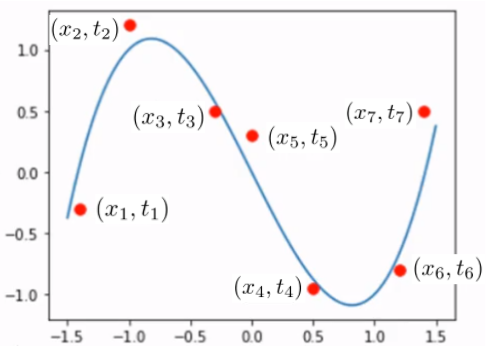
######モデルの定義
予測曲線(モデル)を$y=w_0+w_1x+w_2x^2+\cdots+w_{D-1}x^{D-1}$とする。
######目的関数の定義
あるデータ$(x_i,t_i)$に着目する。
$x_n$の予測値は$w_0+w_1x_n+w_2x_n^2+\cdots+w_{D-1}x_n^{D-1}$である。
$t_n$との差の2乗は$(w_0+w_1x_n+w_2x_n^2+\cdots+w_{D-1}x_n^{D-1}-t_n)^2$である。
これを全データについて足し合わせたものを目的関数とする。
$E(w_0,\cdots,w_{D-1})=\frac{1}{2}\sum_{n=1}^N(w_0+w_1x_n+w_2x_n^2+\cdots+w_{D-1}x_n^{D-1}-t_n)^2$
$\frac{1}{2}$は$w_0,\cdots,w_{D-1}$で偏微分した式を奇麗に見せるためのものである。
######モデルと目的関数を簡潔に表す
${\bf w}=(w_0, w_1, w_2, \cdots, w_{D-1})^T$、
$\phi_i(x)=x^i$、
${\boldsymbol\phi}(x)=(\phi_0(x), \phi_1(x), \phi_2(x), \cdots, \phi_D(x))^T$

とおくと、モデルは $y={\bf w}^T\boldsymbol\phi(x)$ と表せる。

また、目的関数は $E({\bf w})=\frac{1}{2}\sum_{n=1}^N({\bf w}^T\boldsymbol\phi(x_n)-t_n)^2$と書ける。

さらに、$\Phi=\begin{pmatrix}
\boldsymbol\phi(x_1)^T \
\vdots \
\boldsymbol\phi(x_D)^T\
\end{pmatrix},{\bf t}=(t_1,\cdots,t_N)^T$
とおくと
目的関数は $E({\bf w})=\frac{1}{2}||\boldsymbol\Phi{\bf w}-{\bf t}||^2$ と書ける。

######目的関数の最小化
目的関数を最小化するために${\bf w}$で偏微分し、$={\bf 0}$とし、
これについて解くと${\bf w}$が定まり、予測曲線が決定する。
以下導出

\begin{eqnarray}
\frac{\partial}{\partial {\bf w}}E&=&\frac{\partial}{\partial {\bf w}}\frac{1}{2}||\boldsymbol\Phi{\bf w}-{\bf t}||^2\\
&=&\frac{1}{2}\frac{\partial}{\partial {\bf w}}(\boldsymbol\Phi{\bf w}-{\bf t})^T(\boldsymbol\Phi{\bf w}-{\bf t})\\
&=&\frac{1}{2}\frac{\partial}{\partial {\bf w}}({\bf w}^T\boldsymbol\Phi^T-{\bf t}^T)(\boldsymbol\Phi{\bf w}-{\bf t})\\
&=&\frac{1}{2}\frac{\partial}{\partial {\bf w}}({\bf w}^T\boldsymbol\Phi^T\boldsymbol\Phi{\bf w}-{\bf w}^T\boldsymbol\Phi^T{\bf t}-{\bf t}^T\boldsymbol\Phi{\bf w}+{\bf t}^T{\bf t})\\
&=&\frac{1}{2}\frac{\partial}{\partial {\bf w}}({\bf w}^T\boldsymbol\Phi^T\boldsymbol\Phi{\bf w}-2{\bf w}^T\boldsymbol\Phi^T{\bf t}+||{\bf t}||^2)\\
&=&\frac{1}{2}(2\boldsymbol\Phi^T\boldsymbol\Phi{\bf w}-2\boldsymbol\Phi^T{\bf t})\\
&=&\boldsymbol\Phi^T\boldsymbol\Phi{\bf w}-\boldsymbol\Phi^T{\bf t}\\
&&={\bf 0}とすると\\
&&\boldsymbol\Phi^T\boldsymbol\Phi{\bf w}-\boldsymbol\Phi^T{\bf t}={\bf 0}\\
&&\Leftrightarrow \boldsymbol\Phi^T\boldsymbol\Phi{\bf w}=\boldsymbol\Phi^T{\bf t}\\
&&\Leftrightarrow {\bf w}=(\boldsymbol\Phi^T\boldsymbol\Phi)^{-1}\boldsymbol\Phi^T{\bf t}\\
&&\boldsymbol\Phi^T\boldsymbol\Phiは正則であるとする。
\end{eqnarray}

######ソース
こちらからGoogleColabで動作させることができます。

###################################
#  線形回帰 - 曲線フィッティング
###################################
import numpy as np
import matplotlib.pyplot as plt

# 行列φを求める
def get_phi_matrix(N, M, x):
    Phi = np.zeros((N, M))    # N行M列(初期化されていいない)
    for i in range(M):
        Phi[:, i] = x.T ** i  # 1列ずつ格納する Phi[:, i].shape は (N,) なので、xを転置する必要がある
    return Phi;

# 乱数を固定
np.random.seed(1)
# 多項式の最大べき乗数(w0 * x^0+...+wM-1*x^M-1)
M = 4
# 訓練データ数
N = 10

# 訓練データの列ベクトル(N行1列の行列として列ベクトルを表現)
x = np.linspace(0, 1, N).reshape(N, 1)

# 訓練データtの列ベクトル
t = np.sin(2 * np.pi * x.T) + np.random.normal(0, 0.2, N) # sinに正規分布に従う誤差を与える
t = t.T  # 列ベクトルにする(実際にはN行1列の行列) t = t.reshape(N, 1)でもOK

# 行列φを求める
Phi = get_phi_matrix(N, M, x);

# wを解析的に求める
w = np.linalg.inv(Phi.T @ Phi) @ Phi.T @ t

# 求めた係数wを元に、新たな入力x2に対する予測値yを求める
x2 = np.linspace(0, 1, 100).reshape(100, 1) # 点を0から1まで100個、等間隔(1/99)で発生させる

# 行列Phi2を作成
Phi2 = get_phi_matrix(100, M, x2)

# 予測する y = w0*x^0 + ... + wM-1*x^M-1
y = Phi2 @ w     # 正則化無

# 結果の表示
plt.ylim(-0.1, 1.1) # xの表示範囲を制限する
plt.ylim(-1.1, 1.1) # yの表示範囲を制限する
plt.scatter(x, t, color="red")  # 学習データの表示
plt.plot(x2, y, color="blue")  # 正則化無の予測曲線を描画
plt.show()  # グラフ描画

######目的関数は凸関数である
目的関数が凸関数であること示すには、目的関数のヘッセ行列が半正定値行列であることを示せばよい。
以下証明

まず、目的関数のヘッセ行列を求める。

\begin{eqnarray}
\frac{\partial}{\partial {\bf w}}\left(\frac{\partial}{\partial {\bf w}}E\right)&=&\frac{\partial}{\partial {\bf w}}(\boldsymbol\Phi^T\boldsymbol\Phi{\bf w}-\boldsymbol\Phi^T{\bf t})\\
&=&\boldsymbol\Phi^T\boldsymbol\Phi \\
\end{eqnarray}\\

次に、ヘッセ行列が半正定値行列であることを示す。

{\bf x}\in\mathbb{R}^Dとする\\
\begin{eqnarray}
{\bf x}^T\boldsymbol\Phi^T\boldsymbol\Phi{\bf x}&=&(\boldsymbol\Phi{\bf x})^T(\boldsymbol\Phi{\bf x})\\
&=&||\boldsymbol\Phi{\bf x}||^2\geq0\\
\end{eqnarray}\\

目的関数のヘッセ行列は半正定値行列であることが示せた。
よって、目的関数は凸関数である。