Go to Qiita Advent Calendar 2024 Top
LoginSignup
54
41

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@OUDOON(OUDON)

動的計画法の実例: QRコードの最適なエンコードを求める

Last updated at Posted at 2022-08-27

はじめに

最近、実生活で競技プログラミングが役に立ちました。

趣味の一環で長方形のQRコードであるrMQRコードを生成するPythonパッケージを作成しています。その中で「ビット列が最も短くなるようにデータをエンコードする」という処理に動的計画法を用いました。大学時代に競技プログラミングをやっていた身としては「競プロが役に立った！」と嬉しかったので、実例として共有したくてこの記事を書いています。動的計画法のDPテーブルの定義から遷移のしかた、解の復元までを図や実装とともに説明しています。動的計画法自体は説明していません。実装の全体はこちらでご覧いただけます。

この記事に出てくるrMQRコードの仕様に関する記述はISO規格1に基づいています。最適なエンコードを求めるアルゴリズム自体は仕様に含まれるものではなく、オリジナルのものになります。

※QRコードは(株)デンソーウェーブの登録商標です。

rMQRコードの知識

まずは本記事で必要となるrMQRコードの知識について簡単に説明します。

バージョン

QRコードでは大きさごとに名前がついており、これをバージョンといいます。特にrMQRコードの場合は、縦のセル数と横のセル数に応じてバージョンが変わります。縦のセル数を$C_v$、横のセル数を$C_H$としたときに、このバージョンを「R$C_v$x$C_H$」と表記します。例えば、縦が7マスで横が99マスのバージョンは「R7x99」となります。

誤り訂正レベル

データを符号化する際の誤り訂正のレベルを選ぶことができます。rMQRコードでは15％訂正可能なMと、30%訂正可能なHの2種類が使えます。バージョンの最後に誤り訂正レベルを付記して表記することもできます。例えば「R7x99-M」のように書きます。同じバージョンに対しては誤り訂正レベルが高いほうが格納できる文字数は少なくなります。

エンコードモード

rMQRコードではデータをエンコードする際にエンコードモードを指定することができます。 Numeric, Alphanumeric, Byte, Kanjiの4種類が使えます。適切にモードを指定することでエンコード後のビット列の長さを短くすることができます。

モード名 使える文字の種類 エンコード効率
Numeric 0-9 3桁ごとに10ビット
Alphanumeric 0-9 A-Z \s $ % * + - . / : 2文字ごとに11ビット
Byte 任意の文字 1文字ごとに8ビット
Kanji Shift-JISにおける 0x8140 ~ 0x9FFCまたは0xE040 ~ 0xEBBF 1文字ごとに13ビット

Numericモードは数値を効率よくエンコードできるモードです。数字３桁ごとに10ビットで表すことができます。最後のグループが3桁に満たない場合は、1桁なら4、2桁なら7ビットで表されます。

Alphanumericモードは数字と大文字の英字および9つの記号を効率よくエンコードできるモードです。2文字ごとに11ビットで表すことができます。最後のグループが2文字に満たない場合は、1文字を6ビットで表します。

Byteモードはバイト列をそのまま格納するモードになります。そのため任意の文字をエンコードすることが可能です。

KanjiモードはShift-JISにおいて2バイト文字である漢字を効率よくエンコードできるモードです。1文字ごとに13ビットで表すことができます。

セグメント

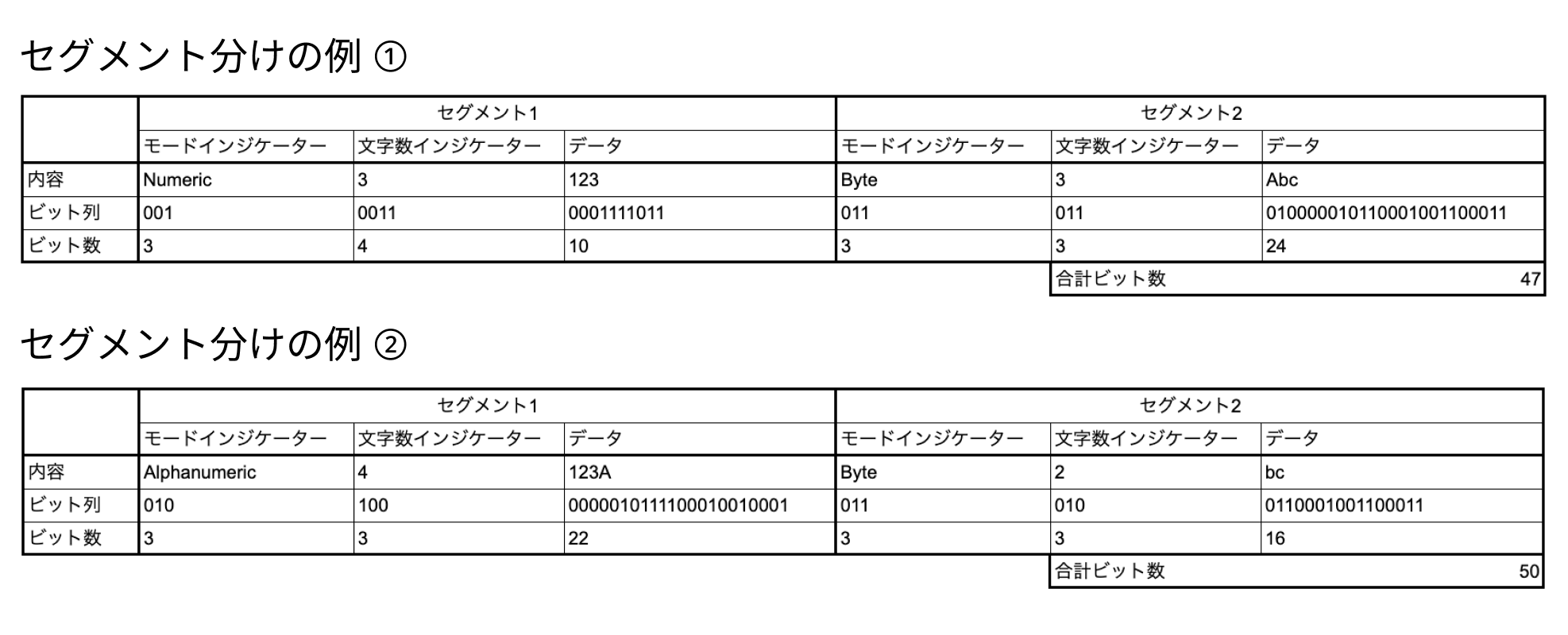
複数のセグメントに分けてエンコードを行うことができます。各セグメントごとにモードを切り替えられます。セグメントはモードインジケーター、文字数インジケーター、データの3つの部分から成り立ちます。例として「123Abc」を2つのセグメントに分けてエンコードした場合を下図に示します。セグメント１は「123」をNumericモードでエンコードしています。セグメント２は「Abc」をByteモードでエンコードしています。２つのセグメントを合わせた全体としてのエンコード後のビット列の長さは47になります。
エンコードの例 - 123Abc ①.png

最適なエンコードを求める問題

rMQRコードではデータを複数のセグメントに分けエンコードを行うことができます。このとき、「どのようにセグメント分けを行うとエンコード後のビット列が最短になるか」を求めることを考えます。エンコード可能なデータの最大は361文字2です。

単純に文字の種類の切り替わりに応じて片っ端からセグメントを分ければ良いと思うかもしれませんが、この方法が最短になるとは限りません。なぜなら、セグメントの先頭にはモードインジケーターと文字数インジケーターと呼ばれるメタデータを付与する必要があるためです。

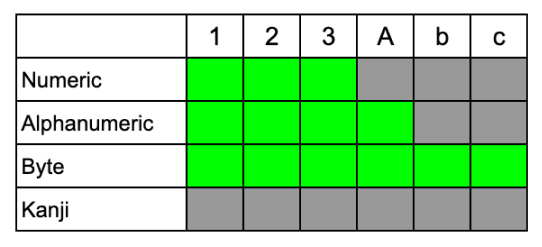
具体例「123Abc」を用いて考えてみます。各文字に対して使用可能なエンコードモードをまとめたものが下図になります。「123」はNumeric, Alphanumeric, Byteが対応しており、「A」はAlphanumericとByteが対応しており、「bc」はByteのみ対応しています。
各文字のエンコードモードの対応表.png

メタデータを付加する必要があることから、隣接するセグメントを同じエンコードモードでエンコードすることは非効率です。そのため、解の候補としては「123Abc」、「123|Abc」、「123A|bc」、「123|A|bc」の4種類の分け方が考えられます。下図に「123|Abc」と「123A|bc」の場合の実際のビット列を載せていますので比較してみてください。この場合の最適なセグメント分けは「123|Abc」になります。
セグメント分け - 2例の比較.png

解法

「１文字ずつ順番にエンコードしていく」と考えます。大きく分けて、注目している文字のエンコードモードが前の文字のエンコードモードと同じか違うかの2つのパターンが存在します。同じモードであれば1文字分の長さが増えるだけです。モードが変わる場合は1文字分の長さに加えてメタデータ分も増えることになります。1文字増やしたときに増えるビット数をコストと考えれば、ナップザック問題と同じように考えることができます。

DPの計算

DPテーブルの定義

DPテーブルを以下のように定義します。

dp[n][mode][unfilled_length] := 先頭からn文字を取り出し、最後の文字のエンコードモードがmodeモードであり、
                                最後のグループのビット数がunfilled_lengthのとき、最小となるエンコード後のビット列の文字数

modeはエンコードモードに対応する0~3の数値です。ここでは、0 => Numeric、１=> Alphanumeric、2 => Byte、3 => Kanjiのように対応しています。unfilled_lengthは最後のグループの文字数です。例えば、Numericモードでは3桁ごとにグループを区切るため、5文字目だとするとunfilled_lengthは2になります。これは１文字増えたときに増えるビット数を計算するために必要になります。

初期化

実装のしやすさから、DPテーブルの初期状態を以下のように定義しました。n=0にはメタデータの長さのみを入れることで、以後の実装で場合分けが減り実装が簡単になります。

dp[0][mode][0] = modeモードにおけるメタデータの長さ

実装はこのようになります。

MAX_CHARACTER = 360
INF = 100000
dp = [[[INF for n in range(3)] for mode in range(4)] for length in range(MAX_CHARACTER + 1)]
parents = [[[-1 for n in range(3)] for mode in range(4)] for length in range(MAX_CHARACTER + 1)]

for mode in range(len(encoders)):
    # エンコードモードに対応するクラス
    encoder_class = encoders[mode]
    # メタデータのうち文字数インジケーターはバージョンによって長さが変わる
    character_count_indicator_length = qr_version["character_count_indicator_length"][encoder_class]
    dp[0][mode][0] = encoder_class.length("", character_count_indicator_length)
    parents[0][mode][0] = (0, 0, 0)

遷移

各n、mode、lengthからすべてのモードへ遷移します。

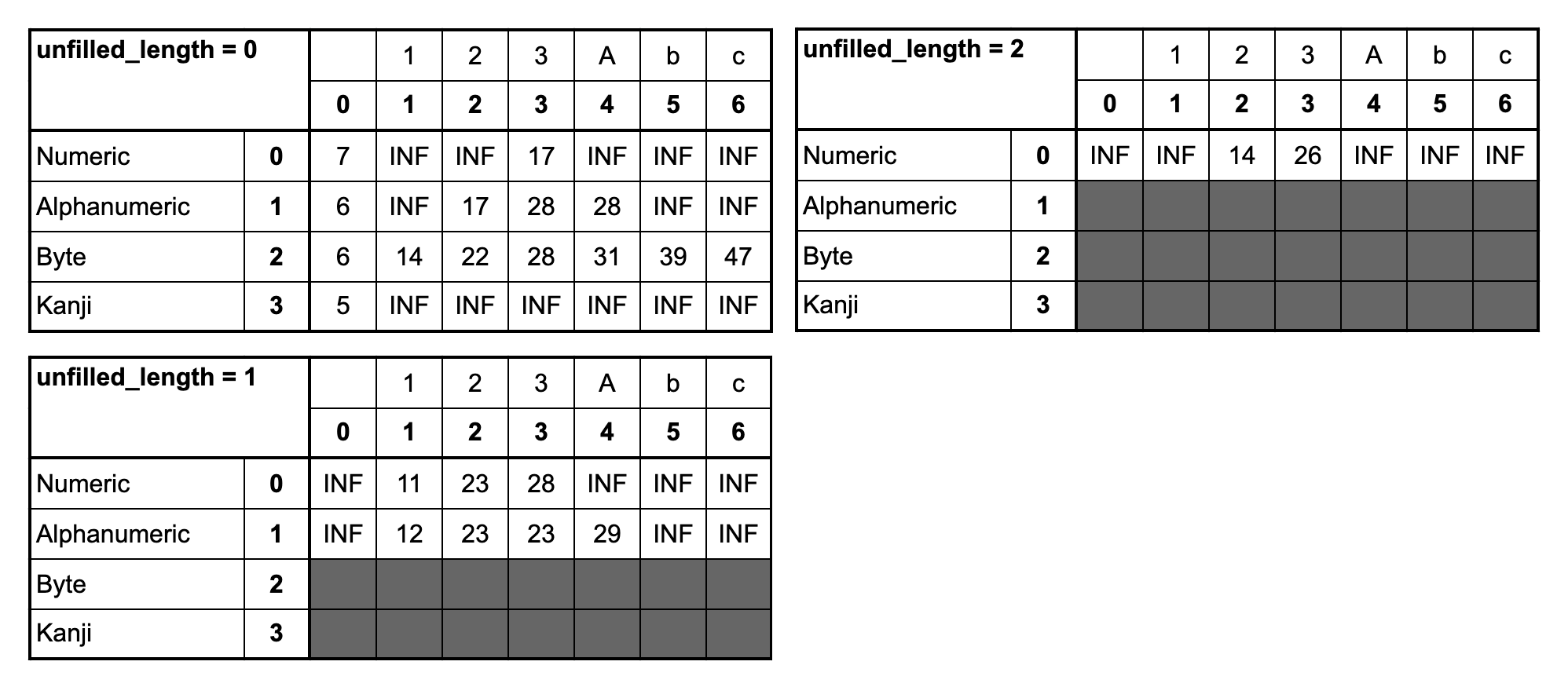
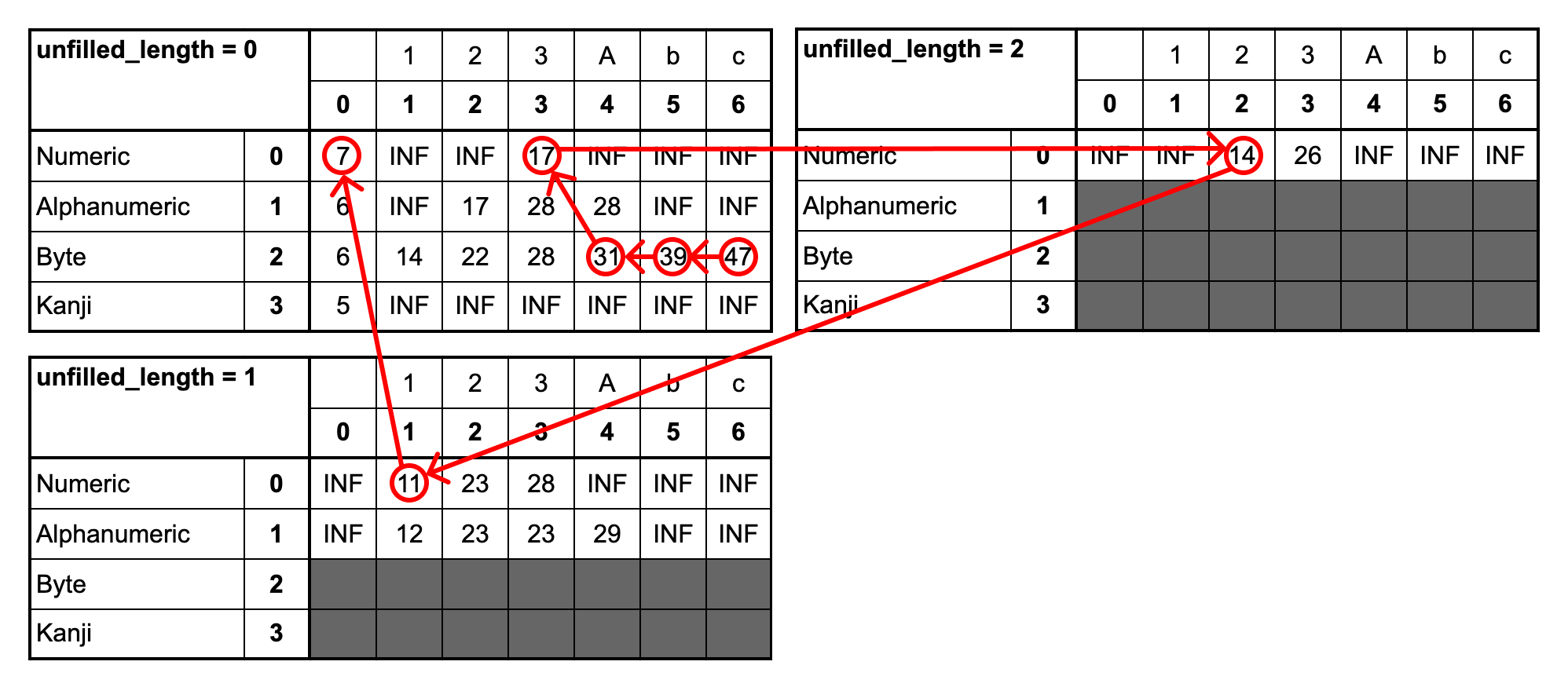
例として「123Abc」のデータに対してDPテーブルを計算した結果を下図に示します。n=6の中で最小のものが最適なビット列の長さということになるので、(n, mode, unfilled_length) = (6, 2, 0)の場合の47が最小のビット列の長さとなります。
DPテーブル.png

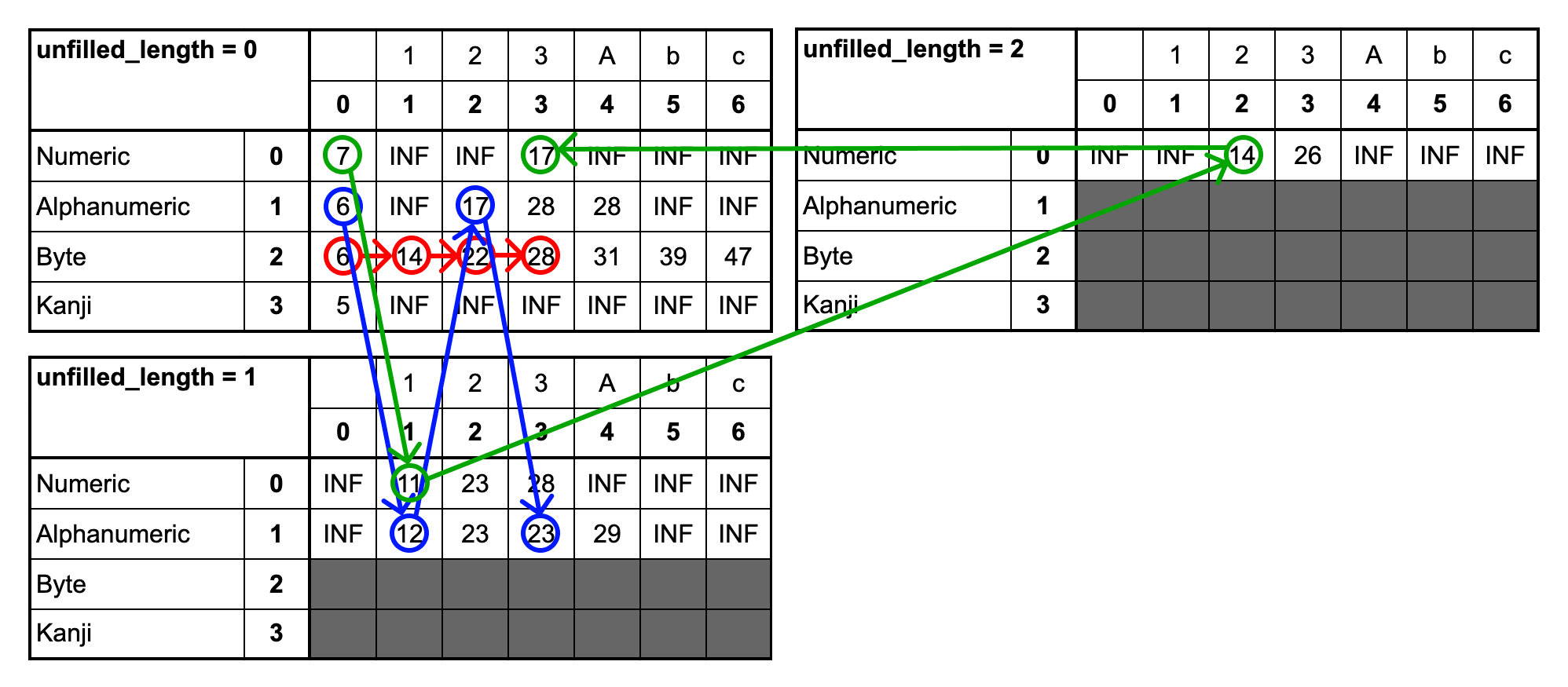
下図はDPテーブルに遷移の例を記載したものになります。緑色の矢印は３文字目までをNumericモードでエンコードをする場合の遷移を示しています。同様に、青色はAlphanumericモード、赤色はByteモードでエンコードする場合に対応しています。Numericモードでは３文字を１グループとするためunfilled_lengthが0→1→2→0⋯と変化していきます。Alphanumericモードでは２文字を１グープとするため、unfilled_lengthは0→1→0⋯と変化していきます。
遷移の例.png

for n in range(0, len(data)):
    for mode in range(4):
        for unfilled_length in range(3):
            if dp[n][mode][unfilled_length] == INF:
                continue

            for new_mode in range(4):
                if not encoders[new_mode].is_valid_characters(data[n]):
                    continue

				# エンコードモードに対応するクラス
                encoder_class = encoders[new_mode]
                # メタデータのうち文字数インジケーターはバージョンによって長さが変わる
                character_count_indicator_length = qr_version["character_count_indicator_length"][encoder_class]
                
                if new_mode == mode:
                    # モードが変わらない場合
                    if encoder_class == encoder.NumericEncoder:
                        new_length = (unfilled_length + 1) % 3
                        cost = 4 if unfilled_length == 0 else 3
                    elif encoder_class == encoder.AlphanumericEncoder:
                        new_length = (unfilled_length + 1) % 2
                        cost = 6 if unfilled_length == 0 else 5
                    elif encoder_class == encoder.ByteEncoder:
                        new_length = 0
                        cost = 8 * len(data[n].encode("utf-8"))
                    elif encoder_class == encoder.KanjiEncoder:
                        new_length = 0
                        cost = 13
                else:
                    # モードが変わる場合
                    if encoder_class in [encoder.NumericEncoder, encoder.AlphanumericEncoder]:
                        new_length = 1
                    elif encoder_class in [encoder.ByteEncoder, encoder.KanjiEncoder]:
                        new_length = 0
                    cost = encoders[new_mode].length(data[n], character_count_indicator_length)

                if dp[n][mode][unfilled_length] + cost < dp[n + 1][new_mode][new_length]:
                    dp[n + 1][new_mode][new_length] = dp[n][mode][unfilled_length] + cost
                    parents[n + 1][new_mode][new_length] = (n, mode, unfilled_length)

解の復元

続いて求めたDPテーブルから解を復元します。解の復元にはparentsテーブルを用います。これはDPテーブルの計算時に最小値を更新した際に、遷移後の状態に行った遷移前の状態を記録しておくというテーブルになります。コードで言うと以下の部分が該当します。

if self.dp[n][mode][unfilled_length] + cost < self.dp[n + 1][new_mode][new_length]:
    self.dp[n + 1][new_mode][new_length] = self.dp[n][mode][unfilled_length] + cost
    self.parents[n + 1][new_mode][new_length] = (n, mode, unfilled_length) # 遷移前の状態を記録しておく

このテーブルを用いて最適解の状態から逆向きにparentsテーブルを辿っていくことで解を復元することができます。「123Abc」の例だと下図のような軌跡が得られます。
復元の軌跡.png

実装はこのようになります。

path = []
index = best_index
while index[0] != 0:
    path.append(index)
    index = parents[index[0]][index[1]][index[2]]
path.reverse()

セグメントのマージ

最後に、得られた解において隣接する同じエンコードモードの領域を一つのセグメントとします。セグメントを変えることでメタデータが付与されるため、同一のモードでセグメントを分けることは明らかに不利だからです。

segments = []
current_segment_data = ""
current_mode = -1
for p in path:
    if current_mode == -1:
        current_mode = p[1]
        current_segment_data += data[p[0] - 1]
    elif current_mode == p[1]:
        current_segment_data += data[p[0] - 1]
    else:
        segments.append({"data": current_segment_data, "encoder_class": encoders[current_mode]})
        current_segment_data = data[p[0] - 1]
        current_mode = p[1]
if current_mode != -1:
    segments.append({"data": current_segment_data, "encoder_class": encoders[current_mode]})

おわりに

動的計画法を用いてrMQRコードの最適なエンコードを求める方法をご紹介しました。大学時代の競技プログラミングの経験を現実世界の問題に適用できたことがとても嬉しかったです。競技プログラミングを始めた頃は、「動的計画法で最小のコストは求まったものの具体的な解はどうやって求めるんだろう」という疑問を持っていました。この実例が具体的な解を求めるまでの一連の流れを理解する役に立てれば幸いです。

題材となったrMQRコードを作成するパッケージのリポジトリはこちらになります。もし気に入れば、スターをつけていただけると励みになります！

なお、このアルゴリズムはrMQRコードでエンコードができる最大の文字数が361文字であることを前提にしています。もしかするともっと効率の良いアルゴリズムがあるかもしれません。そういうアルゴリズムを思いつかれた方はぜひコメントにて教えてください！

  1. ISO/IEC 23941: Rectangular Micro QR Code (rMQR) bar code symbology specification ↩

  2. R17x139, Numericモード, 誤り訂正レベルMの場合に格納できる文字数 ↩

54
41
2

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
54
41

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?