リザバーコンピューティングにおけるリアプノフスペクトルの計算方法

記事の概要

リザバーコンピューティング（Reservoir Computing）¹とは、時系列データを学習し、未来の時系列を予測するRNN（Recurrent Neural Network）の一種です。
また、時系列のダイナミクスの特徴量として、リアプノフスペクトル（Lyapunov Spectrum）と呼ばれるものがあります。リザバーコンピューティングによる予測が元の時系列の統計的な振る舞いを保った予測であるかを定量的に評価するために、このリアプノフスペクトルの概念が用いられます。

本記事では、リザバーコンピュータからリアプノフスペクトルを計算する方法について紹介し、その応用について説明し、数値実験の結果を紹介します。

リザバーコンピューティングのモデル

リザバーコンピューティング¹は、一般的な機械学習と同様に、入力層・中間層・出力層から構成され、特にこの中間層のことをリザバーと呼びます。（詳細については他記事等を参照ください。）
リザバーの状態遷移式は様々な種類がありますが、今回は以下に示すモデルを用います。

\begin{split}
    \boldsymbol{r}(t+1)
    &= \boldsymbol{f}[\boldsymbol{r}(t), \boldsymbol{u}(t)] \\ 
    &= (1-\alpha)\boldsymbol{r}(t) + \alpha\mathbf{tanh}[\mathbf{W}_{\mathrm{res}}\boldsymbol{r}(t) + 
    \sigma \mathbf{W}_{\mathrm{in}}\boldsymbol{u}(t)]
\end{split}
\tag{1}

式内の変数は以下のようなものです。

• 入力次元を$N_u$として、入力データ：$\boldsymbol{u}(t)\in\mathbb{R}^{N_u}$
• リザバーのノード数を$N_{res}$として、リザバーの状態：$\boldsymbol{r}(t)\in\mathbb{R}^{N_{res}}$
• 入力強度：$\sigma$
• 入力層の入力結合重み行列：$W_{in}\in\mathbb{R}^{N_{\mathrm{res}} \times N_u}$
• リザバーのリカレント結合重み行列：$W_{res}\in\mathbb{R}^{N_{\mathrm{res}} \times N_{res}}$
• Leaky Integratorモデルのリーク率：$\alpha \in (0, 1]$

リザバーコンピュータの出力（予測）は、出力層 $W_{out}\in\mathbb{R}^{N_u \times N_{res}}$によって、$\mathbf{W}_{\mathrm{out}} \boldsymbol{r}(t)$ と出力されます。

この出力 $\mathbf{W}_{\mathrm{out}} \boldsymbol{r}(t)$ を入力 $\boldsymbol{u}(t)$ に戻すフィードバックを行うことで、1時刻先より長い予測を行うことが出来ます。したがって(1)式は以下のように変形されます。

\begin{split}
    \boldsymbol{r}(t+1)
    &= \boldsymbol{f}[\boldsymbol{r}(t), \mathbf{W}_{\mathrm{out}} \boldsymbol{r}(t)] \\ 
    &= (1-\alpha)\boldsymbol{r}(t) + \alpha\mathbf{tanh}[\mathbf{W}_{\mathrm{res}}\boldsymbol{r}(t) +     \sigma \mathbf{W}_{\mathrm{in}}\mathbf{W}_{\mathrm{out}} \boldsymbol{r}(t)]
\end{split}
\tag{2}

学習の段階までは真の時系列 $\boldsymbol{u}(t)$ を入力（スイッチ左）し、予測の段階ではフィードバック $\mathbf{W}_{\mathrm{out}} \boldsymbol{r}(t)$ を入力（スイッチ下）します。

リアプノフスペクトル（Lyapunov Spectrum）

リアプノフスペクトルの計算方法については、記事を書きました。リアプノフスペクトルの計算に必要なのは、十分長い時系列データと各点におけるヤコビ行列でした。リザバーコンピュータの状態遷移式、つまり式(1)を高次元の離散力学系であると考えて、この二つを求めます。

• リザバー状態の十分長い時系列データ
  入力時系列に対して、式(1)を繰り返し用いることでリザバーの状態の m 個の時系列 $\boldsymbol{r}(n), \boldsymbol{r}(n+1), \cdot\cdot\cdot, \boldsymbol{r}(n+m-1)$ を得ることが出来ます。このとき、時系列はESP（Echo State Property）によって十分収束してからの時系列を用いることに注意してください。

• 各点におけるヤコビ行列
  ヤコビ行列を求めるため、(2)式を$\boldsymbol{r}(t)$で微分すると、

    \begin{split}
    \mathrm{D}_{\boldsymbol{r}(t)}\boldsymbol{f}[\boldsymbol{r}(t), \mathbf{W}_{\mathrm{out}} \boldsymbol{r}(t)]
    &= (1-\alpha)\mathbf{I} + \alpha (\mathbf{W}_{\mathrm{res}} + 
    \sigma \mathbf{W}_{\mathrm{in}}\mathbf{W}_{\mathrm{out}})^\top \rm{diag}((\mathbf{tanh})'[(\mathbf{W}_{\mathrm{res}} + 
    \sigma \mathbf{W}_{\mathrm{in}}\mathbf{W}_{\mathrm{out}}) \boldsymbol{r}(t)]) \\
    &= (1-\alpha)\mathbf{I} + \alpha (\mathbf{W}_{\mathrm{res}} + 
    \sigma \mathbf{W}_{\mathrm{in}}\mathbf{W}_{\mathrm{out}})^\top \rm{diag}(\mathbf{I}-\mathbf{tanh}^2[(\mathbf{W}_{\mathrm{res}} + 
    \sigma \mathbf{W}_{\mathrm{in}}\mathbf{W}_{\mathrm{out}}) \boldsymbol{r}(t)])
    \end{split}
\tag{3}

　ここで、$\mathbf{I}$ は単位行列を表します。一行目の変形では、ベクトルの合成関数のベクトル微分を行っていることに注意してください。また、ベクトル微分の表記として、分母レイアウト記法 (Denominator Layout)を用いています。二行目の変形は、$\mathbf{tanh}$ の微分公式を用いました。

十分長い時系列データと各点におけるヤコビ行列が求まったので、あとは記事に従ってリアプノフスペクトルを求めることが出来ます。

応用例

リザバーコンピュータから計算したリアプノフスペクトルの応用例について紹介します。

リザバーコンピュータによる予測の力学的性質の再現性の評価²

リザバーコンピューティングの理論では、入力時系列を高次元空間であるリザバー層に入力し、十分な時間発展ののちに、入力が元の空間からリザバー空間への埋め込みであることを期待します。しかし、埋め込みに成功し、短期予測には成功していても、元の時系列のエルゴード的（統計的）な性質を保っているとは限りません。そこで、元の時系列のリアプノフスペクトルとリザバーコンピュータから計算したリアプノフスペクトルを比較することで、その再現性を定量的に評価することが出来ます。
この場合、十分長い時系列データとして用いるのは(2)式、つまりフィードバックによるリザバーの状態の時系列であり、(3)式を計算する際の $\boldsymbol{r}(t)$ にもこのフィードバックによる時系列を用います。

学習済みのリザバーコンピュータの同期の評価³

リザバーコンピューティングの理論では、リザバー空間を入力時系列に駆動される応答系と考えて、入力時系列とリザバー空間の間に同期（弱い一般化同期）が成立していることを期待します。この同期が成立しているとき、リザバーによる予測は元の時系列のエルゴード的（統計的）な性質を保った予測が出来ていると考えられます。この同期の定量的な評価・安定性の評価⁴にリアプノフスペクトラムを用いることが出来ます。

上記の評価方法と異なり、リザバーの状態の十分長い時系列データは、(1)式、つまり真の時系列入力下で求めたものを用います。各点におけるヤコビ行列は、(3)式を計算する際の $\boldsymbol{r}(t)$ にもこの時系列を用います。

数値実験

実際に、学習済みのリザバーコンピュータの同期の評価 を実験してみます。元の時系列のエルゴード的（統計的）な性質を保った予測が出来ているかどうかは、プロットして目👀で見て確かめましょう。
Lorenz方程式で数値実験を行った結果を示します。パラメーターは $p = 10、r = 28、b = 8/3$ を用いました。この時の真のリアプノフスペクトルは $[0.91, 0, -14.6]$ です。

真のLorenzアトラクタ

よく見る蝶々型のストレンジアトラクタを形成します。真のリアプノフスペクトルは $[0.91, 0, -14.6]$ です。

真値と異なるリアプノフスペクトルをもつリザバコンピュータの予測結果

予測に失敗してるといえます。（短期予測には成功しているが、、、）このとき、学習済みのリザバーから計算されたリアプノフスペクトルは $[0.1569,-0.01747,-0.2967, \cdot\cdot\cdot]$ でした。

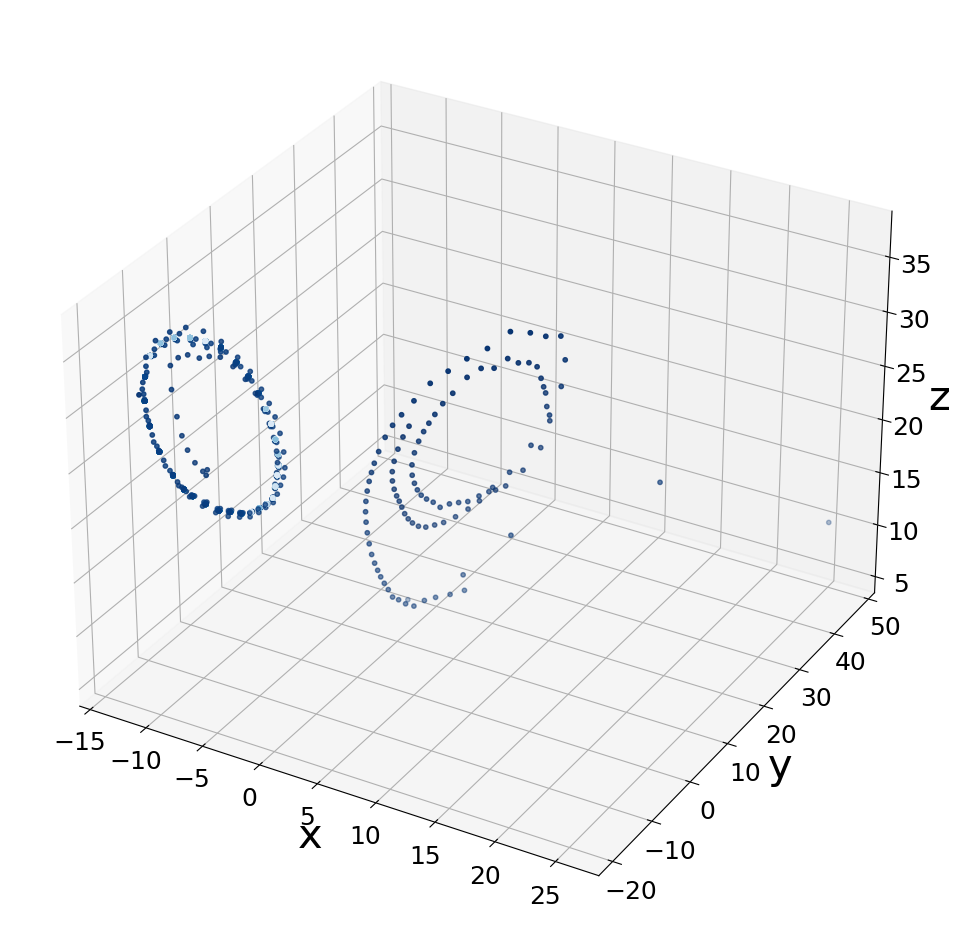
真値に近いリアプノフスペクトルをもつリザバコンピュータの予測結果

真の系と類似したアトラクタを形成しています。このとき、学習済みのリザバーから計算されたリアプノフスペクトルは$[0.9165,-0.00944,-0.0859, \cdot\cdot\cdot]$ でした。

以上の結果から、リザバーコンピュータから計算したリアプノフスペクトルは元の時系列のエルゴード的（統計的）な性質の再現性を定量的に評価する指標として用いることができると分かりました。

いかがでしたか？

この記事が気に入ったなら是非、記事の上下にあるいいね💛を押して下さいね！それでは皆さんもぜひ、リザバーコンピュータからリアプノフスペクトルを計算してください！！！

1. http://www.scholarpedia.org/article/Echo_state_network
   （調べれば日本語でも記事があります） ↩ ↩²

2. Pathak, Jaideep, et al. "Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data." Chaos: An Interdisciplinary Journal of Nonlinear Science 27.12 (2017): 121102.
   （エルゴード的（統計的）な性質を保った予測が出来ていることを確認するため、元の時系列のリアプノフスペクトルとリザバーコンピュータから計算したリアプノフスペクトルを比較し評価した論文） ↩

3. Lu, Zhixin, Brian R. Hunt, and Edward Ott. "Attractor reconstruction by machine learning." Chaos: An Interdisciplinary Journal of Nonlinear Science 28.6 (2018): 061104.
   （学習済みのリザバーコンピュータから計算したリアプノフスペクトルを分析するとアトラクタ再構成の達成が分かる、という内容の論文） ↩

4. 元の時系列のリアプノフスペクトルとリザバーコンピュータから計算したリアプノフスペクトルを比較することで、同期を評価できるが、特に、同期の安定性を横断リアプノフ指数(transeverse lyapunov exponent: 同期多様体から指数的に離れる速さ) の正負で評価できます。詳細は上記の論文を参照 ↩