問題概要

picoCTF 2022の最難関Crypto問題である。
この問題では、以下の式からflagを求める必要がある。
$$ c = 3^{flag} \mod n $$
一般に、この問題は離散対数問題と呼ばれる。

解法

参考にした論文

ここでヒントを見てみよう。

Look for Mr. Wong's whitepaper... His work has helped so many cats!

この情報をもとに検索をしてみると、以下の論文を発見した。

https://eprint.iacr.org/2016/644.pdf
この論文をヒントに、この問題を解いてみよう。

小問題への分解

先の論文に、以下の図があった。

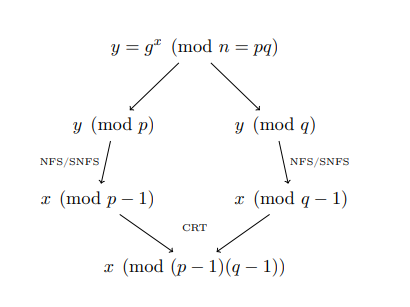
出典: https://eprint.iacr.org/2016/644.pdf (2022/4/2アクセス)
この図は
$$ g^x \mod n $$
からxを求めるという大きな問題を、
$$ g^x \mod p $$
$$ g^x \mod q $$
からxを求める問題へと分解し、中国剰余定理(Chinese Reminder Theorem)で元の問題の答えを導くことを示している。

また、上記の問題も、以下の小問題に分割できる。

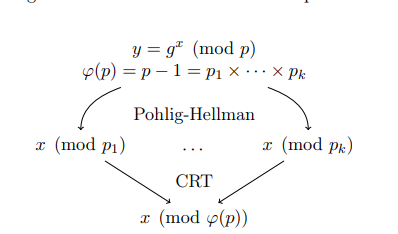
出典: https://eprint.iacr.org/2016/644.pdf (2022/4/2アクセス)
要するに、pを法とした問題は、p-1の素因数を法とする小問題に分割できるということだ。
すなわち、次の目標はp-1、q-1をそれぞれ素因数分解することである。

p-1、q-1の素因数分解

では、巨大な数であるp-1、q-1をどのような方法で素因数分解すればよいのだろうか。
実は、以下のアルゴリズムで素因数分解が可能である。

出典: https://montoguequiz.com/electrical/rsa-public-key-pollard-algorithm/ (2022/4/2アクセス)
上記のアルゴリズムを実装した関数が以下である。

def find(n):
    alpha = 2
    beta = 2
    while True:
        alpha = pow(alpha, beta, n)
        d = gmpy2.gcd(alpha - 1, n)
        if 1 < d and d < n:
            print(f"{d}, ", end="")
            n //= d

            if d == 1:
                return
            else:
                find(n)
        else:
            beta += 1

この関数から得られたp-1、q-1の素因数をもとに、p-1、q-1を素因数分解した。
その結果を以下に示す。

p_factor_lst = [2, 33479, 35027, 35677, 35729, 35869, 35963, 37423, 37529, 37607, 38231, 38699, 40099, 40351, 41257, 41947, 42859, 43271, 43793, 44449, 44483, 45281, 45491, 46861, 47207, 47543, 48221, 48563, 50227, 50273, 50503, 50891, 50969, 52081, 53623, 53657, 54917, 55147, 56003, 56131, 56957, 56989, 57329, 58679, 59263, 60013, 60127, 60703, 63067, 63719, 63949, 64849, 65029, 457311223, 690080687, 1753837567, 1934186953, 2264412959, 2800733603, 3331168403]
q_factor_lst = [2, 25763, 27539, 68071, 68437, 69239, 69809, 71411, 71777, 74923, 75079, 77417, 78779, 79357, 83417, 83497, 83639, 85889, 86491, 86711, 87583, 88681, 88883, 89561, 89653, 89809, 95257, 95819, 98179, 99149, 103991, 104369, 104459, 105727, 106087, 106823, 109321, 109819, 110431, 110681, 111187, 111301, 112397, 114041, 118033, 120503, 120689, 122399, 123701, 124513, 127691, 6496959103, 7564474987, 9206469053, 11978812487, 12402637831, 15850128317]

小問題を解き、元の問題の答えを出す

さて、それぞれの素因数に対し、
$$ g^x \mod (素因数) $$
からxを求める小問題を解き、元の問題の答えを求めよう。
まず、p-1、q-1に対して以下のスクリプトを実行した。
なお、以下のスクリプトは自分で書いたものではなく、他人が書いたものをpython3用に改変したものである。

from functools import reduce
def egcd(m, n):
    if n>0:
        y,x,d = egcd(n, m%n)
        return x, y-m//n*x, d
    else:
        return 1, 0, m


def modinv(a, m):
    (inv, q, gcd_val) = egcd(a, m)
    return inv % m


def chinese_remainder(Q, X):
    P = reduce(lambda x,y: x*y, Q)
    result = 0
    for i in range(len(X)):
        x, y, d = egcd(Q[i], P//Q[i])
        result += y*(P//Q[i])*X[i]
    return result % P


# Baby-step giant-step
def baby_step_giant_step(g, y, p, q):
    m = int(q**0.5 + 1)
    
    # Baby-step
    baby = {}
    b = 1
    for j in range(m):
        baby[b] = j
        b = (b * g) % p

    # Giant-step
    gm = pow(modinv(g, p), m, p)
    giant = y
    for i in range(m):
        if giant in baby:
            x = i*m + baby[giant]
            print("Found:", x)
            return x
        else:
            giant = (giant * gm) % p
    print("not found")
    return -1


# Pohlig-Hellman algorithm
def pohlig_hellman(p, g, y, phi):
    Q = phi
    print("[+] Q:", Q)
    X = []
    for q in Q:
        x = baby_step_giant_step(pow(g,(p-1)//q,p), pow(y,(p-1)//q,p), p, q)
        X.append(x)
    print("[+] X:", X)
    x = chinese_remainder(Q, X)
    return x

x_p = pohlig_hellman(p, g, c, p_factor_lst)
x_q = pohlig_hellman(q, g, c, q_factor_lst)

出典: https://sonickun.hatenablog.com/entry/2016/11/20/192743 (2022/4/2)
x_p、x_qにはそれぞれ
$$ g^x \mod p $$
$$ g^x \mod q $$
に対しての答えが入っている。
あとは、この二つの答えを中国剰余定理で統合すればよい。

from Crypto.Util.number import *
long_to_bytes(chinese_remainder([p, q], [x_p, x_q])).decode()

これにより、flagを求められた。

使用ライブラリ

jupyter notebook
gmpy2
pycryptodome

picoCTF2022 NSA Backdoor 日本語Writeup