オセロの最短引き分けを探す夏休みの自由研究

Last updated at 2024-08-02Posted at 2024-07-30

最近、知り合いのオセラー(オセロプレイヤ)から、オセロにおいて20手の引き分けがあるという情報をいただきました。オセロは大抵60手で終局するので、20手で引き分けというのは非常に特殊な状況です。というわけで、今日は夏休みの自由研究がてら、オセロにおける最短引き分けを探すことにしました。

2024/08/01にバグ報告をいただき、20手引き分けにチェック漏れがあることがわかりました。2024/08/02にバグを修正し、それに伴い記事を修正しました。

とりあえず結論を知りたい人向け

私の証明に穴がなければ、最短引き分けは20手で、10種類の終局結果・185個の棋譜がありました。10種類それぞれの終局結果について1つずつ棋譜を掲載します。なお、終局結果は線対称・点対称・回転対称を同一視し、棋譜は全てf5始まりに統一してあります。

f5f4c3f6g7f7f3h7f8b2h6e7h8e3d7g3f2f1a1c5
f5f4c3f6g7f7f3h7f8b2h6e7h8e3d7g2f2f1a1c5
f5f4c3f6g7f7f3h7f8b2h6e3a1e7f2f1h8e2d7c5
f5f6e6f4g7c6f3g2f2f7b7a8h2f1f8h3e2h1c4d2
f5d6c6b6b7f6b5a6e6a8b8f3f7g6g2c8h6h1d3b4
f5d6c6b6b7f6b5a6f7f3g2b4e6g6b3h1h6a8d3b2
f5f6e6f4g5c6f3g2f2f7b7a8h2f1f8h3e2h1c4d2
f5f4g3e6c4b3b4g4f7g8b2a2h4b5b6a4d7b7d6b1
f5f4g3e6c4b3b4g4b2a4f7c2h4g8d2d1d7e2d6a2
f5f4g3e6c4b3b4g4f7g8b2a2d6b5b6c2h4a4d7b7

それぞれの棋譜を並べると下図の終局となります。全て黒白共に12石同士で引き分けとなっています。

今回、計算機を使ってこれらの結果を求めました。コードはGitHubで公開しています。

冒頭に書いた通り、実は20手引き分けの棋譜は1つすでに(人力探索で！)見つかっていました。それが4つ目の棋譜です。実際に初手から石を並べると、「確かに引き分けになるが、なんでこれを人力で発見できたんだろう…」という気持ちになります。すごすぎます。人力探索についてはこちらの記事でご本人が詳しく解説されているので、ぜひご覧ください。

オセロの終局とは

オセロでは、64マスの全てが埋まるともちろん終局ですが、一部のマスが空いている場合でも、黒白どちらもそのマスに打てない場合は対局終了です。下図の局面は1マス(h7のマス)が空いていますが、黒も白もそのマスに着手できません。こういうときは1マス空いた状態で終局です。

ちなみに、終局したときに空いているマスは、勝者の石としてカウントします。ですので、例えば下の局面は黒が13石、白が0石で終局(最短全滅です)ですが、これは空いている51マスを全部黒の石として、黒が白よりも64石多いとカウントします。

なお、終局したときに黒も白も石数が同じであれば、引き分けになります。今回は引き分けでの終局を考えるので、空いているマスのカウントについては深く考えなくてOKです。

計算量を考える

オセロというゲームは、単純に見えて実は考えうる局面は非常に多く、例えば序盤12手を打つだけで10^8個を超える局面が現れます(オセロの序盤の展開数より)。今回、事前情報として知っているのは20手以内に引き分けが存在するということだけです。ですので、最大で20手まで全ての手を展開することになります。

オセロの中盤は大体1つの局面あたり10手程度の合法手が存在するので、20手まで手を展開すると、確認すべき局面(計算量)は10^16程度(10^8(12手)から8桁増えた)になると予想できます。これでは多すぎて計算が終わりません。そこで、計算量(正確には計算回数)を落とす工夫が必要になります。

スカスカで引き分けに終わるという特徴を使って高速化する

オセロの最短引き分けを見つけるのは、愚直に計算するとまともな時間では終わりません。そのため、まあなんとか待てるくらいの時間で計算を完了できるように方針を考えます。

空きマスがいっぱいある状態のまま引き分けで終局する場合、終局した盤面は特殊な条件を満たす必要があります。今回は、この条件を利用して終局盤面の候補を先に列挙して、その後に初期盤面から終局盤面に到達できるかを確認するという方針を取ると大幅に高速化ができます。

どちらかが全滅すれば、双方の打てるところは自明になくなるので、終局です。しかし、今回は盤面がスカスカのまま、引き分けで終局します。つまり黒と白のどちらの石も盤上にあるまま、双方打てる場所がなくなるということです。これを満たすために必要なことを考えます。

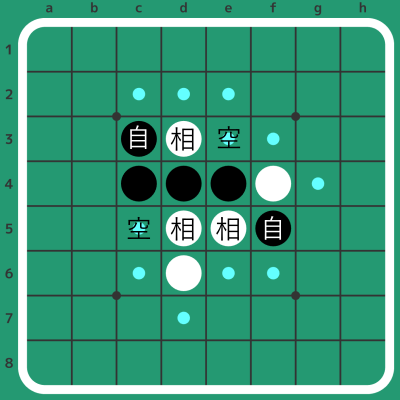
オセロでは、「自分の石で相手の石を挟める場所に着手できる」というルールがあります。説明に下図を使います。下図は黒の手番で、置けるところ(合法手)に水色の点を描いてあります。この図を見ながら改めて「自分の石で相手の石を挟める場所」について考えると、自分の石、相手の石(1つ以上)、空きマスがこの順番で一直線に並んでいる場合、空きマスが合法手となる(空きマスに自分の石を置くと相手の石を挟める)と言えます。

今回は空きマスがある状態での終局なので、「黒石も白石も盤上にあるのに、双方のプレイヤがどこにも置けない」という状況になります。上で考えた内容を黒白双方について考えると、黒石と白石が接している直線上のどこかに空きマスがあると、黒側または白側で必ず合法手が生じてしまう(終局しない)と言えます。ですので、引き分け終局では黒石と白石が接しているときは、その直線上に空きマスはないことが満たされます。

引き分け終局では黒石と白石が両方盤上に存在するため、盤上のどこかで黒石と白石が接している場所が必ずできます。そのため、引き分け終局の盤面では必ず1本以上の埋まっているラインがある(石で一直線全部埋められている)とわかります。最短終局を見つけるには、この条件を満たす終局盤面を生成して、その後に初手からその局面に到達できるかどうかを確認すると良いです。

方針

上記の工夫を踏まえて、最短引き分けを探すための方針を立てます。

「最短の引き分け」を探したいので、まずは1手の引き分けを探して、1手で引き分けがなければ次に2手の引き分けを探して、次は3手、4手…と順番に深さを増していって探索を行います。これを反復深化と言ったりします。ただし、引き分けで終局する(黒白双方の石数が同じ)ときは必ず偶数手の着手で終わるため、実際は2手、4手、6手…と2手ごとに見ていきます。

$d$手で引き分ける手筋を探すときは、以下の手順を踏みます。

終局時の石の配置(シルエット)を作る
- 黒と白は区別しない
- $d+4$個の石を盤上に置く
- 1つ以上のラインが石で埋まっていることが条件
シルエットの中で黒石と白石の配置(終局盤面)を考える
- 引き分けなので、黒と白の石数は同じ
- 終局盤面では黒白共に合法手が存在しない
初期局面から終局盤面に到達できるかを考える
- 以前作ったオセロの棋譜探索アルゴリズムを使う

それぞれの手順について詳しく解説します。

1. シルエットを作る

シルエットを作るときには、1つ以上のライン(盤面の端から端までの一直線)を石で埋める必要があります。そのため、あらかじめ埋めるべきラインを決めておいて、ライン以外の部分の埋め方を考えるようにします。使用するラインは下図の11通りです。これらのラインのそれぞれについて、初期盤面の中心4マス分も埋めた状態(初期シルエット)から探索を開始します。なお、線対称・点対称・回転対称は除いて考えてOKです。

なお、一番右下の2マスのラインは、もう少し計算量を減らす工夫をしました。ややこしいので詳細は割愛します。

オセロでは、そのルールの特性上、8近傍(縦横斜めの隣り合ったマス)を辿ることで任意の石から任意の石までたどり着くことができます。つまり、下図のように石の塊が分裂した状態は作れません。

そのため、初期シルエットから石を追加していくときは、現在のシルエットから8近傍で隣接している空きマスにのみ石を追加するようにします。さらに言えばもう少し置ける場所を削減できるのですが、その解説は割愛します。

2. 黒石と白石の配置(終局盤面)を考える

シルエットが完成したら、そのシルエットに対して黒石と白石を配置します。このときにも、「終局状態で黒石と白石が接している場合、そのラインは全て石で埋まっている必要がある」という定理が役立ちます。この定理を使うと、確実に同じ色になる石をまとめたグループがいくつかできます。あとはこれらのグループを黒石にするか白石にするかを考えます。最終的に、黒石と白石の数が同じようになる局面ができればOKです。

3. 初期局面から到達できるかを確認する

石の配置を決めたら、あとはオセロの初期局面からその終局結果に到達できるかどうかを確認します。このアルゴリズムは私が以前作ったものを流用しました。軽くアルゴリズムの概要を述べます。

棋譜探索アルゴリズムでは、初期局面からあらゆる合法手を打っていき、与えられた局面に到達するかどうかをチェックするという単純な方法で探索を行います。しかし、これも計算量削減のためにいくつかの工夫を施してあります。

ある局面$B$が与えられたとき、初期局面から$B$に到達するためには、$B$で石が置かれているマスのみに着手する必要があります。これは、オセロでは空きマスに石を置いたら必ず終局までその石はそのマスに存在し続けるからです。途中でひっくり返されて色が変わる可能性はありますが、石のあったところが空きマスになることはありません。この制約によって、考えるべき合法手数を減らすことができます。

また、確定石という概念を使ってさらなる高速化が可能です。オセロでは対局中の局面において、今後終局まで絶対にひっくり返されることのない石が存在することがあります。こういった、絶対にひっくり返されない石を確定石といいます。隅に石を置くとその後ひっくり返されないというのは、隅に石を置くとその瞬間にそれが確定石になるという意味です。棋譜探索では、探索過程の局面$C$において、確定石を計算します。ここで求めた(いくつかの)確定石の色が、どれか一つでも与えられた局面$B$の石の色と違えば、$C$から$B$へは到達できないとわかり、この時点で探索を打ち切れます。実装上は高速化のため、与えられた局面において隅として働く(石を置いた瞬間にその石が確定石となる)マスをあらかじめ列挙しておくなどの工夫をしました。例として、下の図では隅として働く石に星をつけてあります。

4時間かけて計算する

あとはこれらのアルゴリズムを実装して、実行するのみです。

今回はC++を使ってプログラムを書きました。全体を通して、オセロ盤はビットボードを使って表現しました。これによって非常に高速な探索が可能になります。なお、オセロのボード操作などの部分は私の作ったオセロAI Egaroucidから借用しました。

Egaroucidから借用した部分を除くと、全体は600行程度になりました。メインのコードはこちらです。

これを実行すると、最短引き分けが求められます。得られた結果は冒頭に書いた通りで、20手が最短引き分けであるとわかりました。

f5f4c3f6g7f7f3h7f8b2h6e7h8e3d7g3f2f1a1c5
f5f4c3f6g7f7f3h7f8b2h6e7h8e3d7g2f2f1a1c5
f5f4c3f6g7f7f3h7f8b2h6e3a1e7f2f1h8e2d7c5
f5f6e6f4g7c6f3g2f2f7b7a8h2f1f8h3e2h1c4d2
f5d6c6b6b7f6b5a6e6a8b8f3f7g6g2c8h6h1d3b4
f5d6c6b6b7f6b5a6f7f3g2b4e6g6b3h1h6a8d3b2
f5f6e6f4g5c6f3g2f2f7b7a8h2f1f8h3e2h1c4d2
f5f4g3e6c4b3b4g4f7g8b2a2h4b5b6a4d7b7d6b1
f5f4g3e6c4b3b4g4b2a4f7c2h4g8d2d1d7e2d6a2
f5f4g3e6c4b3b4g4f7g8b2a2d6b5b6c2h4a4d7b7

実行には私のパソコン(Core i9-13900K)で4時間かかりました。現実的な規模の計算ですね！(？？？) 今回は並列化をしませんでしたので、うまくタスクを分散して並列化すれば10倍速くらいは達成できそうですが、まあ今回は寝ている間に計算してくれたので、良しとします。

実行結果の生データ

実験結果の生データをGitHubに公開しています。