今朝起きたら、とんでもない論文を見つけました。
Othello is Solved
ゲームの オセロが"解かれた(弱解決)" というのです。飛び起きました。それで、16時まで二度寝してから読みました。
注意すべきは、この論文が査読を経て公開されているわけではないこと、つまり形式上特にチェックを受けたものではないことです。ただ、タイトルからして非常に衝撃的ですので、個人的に読んでみました。この記事では、私がこの論文(およびソースコード)を読んでわかったことを、なるべくわかりやすくまとめます。随時更新します。
余談ですが、このタイトルはどうやら、チェッカーというゲームが以前弱解決された際の論文"Checkers Is Solved"のオマージュだろうという話です。
この記事には専門用語が出てくるので、最後の方に基礎知識として重要な用語や知識をまとめました。
お知らせ
最初にお知らせしておくべきことをここに書きます。
この記事の立ち位置
この記事は、論文Othello is Solvedとは無関係の人がこの論文を読んで理解したことを解説し、軽く感想を書いたものです。私はオセロAI制作を独自に頑張っており、それなりに知識があると願っていますが、この記事は間違いを含む可能性もあります。ご了承ください。また、間違いは適宜修正し、大きなミスの修正は「お詫びと訂正」でアナウンスしています。
別記事の紹介
なお、この記事は内容をかなり詳しく書いていますし、適宜追記しているので読みにくいと思います。この記事とは別に、私がOthello is Solvedについて短く解説した記事が情報処理学会のnoteで公開されておりますので、よろしければご覧ください。
「オセロが解けた」を白黒ハッキリさせようじゃないか - 情報処理学会・学会誌「情報処理」特別解説
お詫びと訂正
この記事の内容は、私が読解した結果を解説したもの、私の解釈、感想などです。内容は間違っている場合があります。ご了承ください。また、間違いやわかりにくいところなどの指摘をぜひお願いします。
以下、すでに訂正した間違いの概要を列挙します。
2023/11/06 17:10 Algorithm 1において、「ドメイン知識を使う」という解釈が全体的に間違っていました。ちなみに論文本体のDiscussion and Conclusionに、ドメイン知識を使うという発想も書かれています。
2023/12/29 21:40 Algorithm 1の説明において、引き分けを証明するために確認しなくてはいけない局面は少なく済む理由の説明が若干間違っていたので修正し、さらにわかりやすい表現に改めました。
自己紹介
2021年よりオセロAI開発をしています。にゃにゃんです。私のオセロAIはEgaroucidと言って、世界最強クラスのものです。
元々CodinGameのオセロAIでオセロAIを作り始め、そこで世界1位になりました。
結論: 私が読んでわかったこと
私がこの論文を読んだ結果、おそらくこの手法であれば(実装ミスがなければ)オセロを弱解決できるだろうと思いました。
つまり、初期局面から双方が(厳密に)最善の手を打てば、その対局は引き分けになるというのです。
ここで気をつけるべきなのが、弱解決であるという点です。簡単に言えば、対局において相手がどんな手を打っても、こちらは厳密な最善で返せますが、自分がミスをした(悪手を打った)結果発生した局面について、厳密な最善手がどれなのかは求めていないということです。多分この文章だけではよくわからないと思いますので、弱解決について詳しくは基礎知識のところで解説します。
提案手法と実験結果の解説
論文内で 3. Methods と 4. Results として書かれている内容の解説です。つまり、メイントピックの解説です。
提案手法のポイントを私が(私の理解の範囲で)一言で表すと、
生真面目に計算しては途方もない時間がかかることを、「多分こうなるからそういうことにしてとりあえず話を進めよう」という考えを用いることで、現実的な時間で終わらせた
という点だと思います。オセロを初期局面から読み切り、弱解決をする(60手という深さを読む)ことは、ただただ真面目にやっていてはいつまで経っても終わりません。そこで、10手とか、14手とか、浅い深さの探索を行って、厳密な評価値(結果)ではなく推測した評価値を使って探索を行うことで、とりあえず時間の問題を解決しました。しかし、これだけでは当然、厳密にオセロが引き分けとは言えません。そこで、浅い探索をした後に、浅い探索で結果を推測した局面(最初の局面よりも手が進んで、厳密な探索をしやすくなった)をまとめて探索して、厳密な結果を得ます。もしかしたら、推測した結果が間違っているとわかるかもしれません。そんなときは、厳密な結果を使いつつ浅い探索をもう一度やり、また厳密な探索をして…と繰り返すと、徐々に浅い(推測の域を出ない)探索だったものが、厳密な探索へと変わっていきます。
提案手法は、私が思うに、3種類の要素に分割できます。カッコ内のAlgorithm Xという名前は論文内で使われているアルゴリズムの番号です。
- Algorithm 1 : 初期局面から10手(50マス空きまで)の浅い探索(推測を使う)をする
- Algorithm 2-5 : 50マス空きから36マス空きまで14手の浅い探索(推測を使う)をする
- Algorithm 6 : 浅い探索と厳密な終盤探索を交互に繰り返し、浅い探索の結果を厳密なものであると証明する
「何を言っているんだ」という話ですので、詳しく説明します。
そもそもオセロは引き分けになるだろうと言われていた
通常のオセロは8x8ですが、実は4x4、6x6の縮小したオセロは、すでに解かれていました。その結果はどちらも後手(白)必勝です。さて、そんな経緯があって、昔(話に聞くところだと2000年以前?)は8x8も後手必勝だろうと言われていたこともあったようです。
しかし、特に最近は個人で使えるオセロの解析ソフト(それこそEdaxであったり、拙作Egaroucidであったり)とパソコンやスマホの計算パワーが発達して、個人でもかなり精度良くオセロの評価値が確認できるようになってきました。
その結果、だんだんと「8x8の通常のオセロは双方ミスをしなければ引き分けになりそう…?」と思う人が増えたようです。特に人力でオセロを打つオセラーの方々はその考えが強いように思います。私自身オセラーの端くれですが、私自身も含めほとんどのオセラーが「オセロはほぼ確実に(双方ミスをしなければ)引き分け」と思っているようです。
この論文では、なるべくドメイン知識を使わないようにオセロを解いたようですが、この引き分けであろうという知識は使ったようです。オセロを「解く」には、本当は「どちらがいくつ石が多く勝つか」という情報を含めるべきと言われます。ただ、8x8のオセロはおそらく引き分けなので、論文では、黒必勝・白必勝・引き分けのみの結果がわかるように探索しています。これでもしどちらかが必勝であれば、黒と白でどちらがいくつ石を多く獲得できるのか調べる必要がありますが、引き分けであるという結論が出れば、それ以上調べる必要がありません。
一般に、「必勝または引き分け」を求めることは「どちらがいくつ石を多く獲得できるか」を求めるよりも簡単です。この論文では、そういった知識を用いたようです。
なお、論文の実装では評価値が-1から1の範囲に絞って探索する、専門的にはaspiration searchと呼ばれる手法を用いて上記のアイデアを実現しています。
実は、この論文の著者は最初、オセロが本当に引き分けになるのか確証がなかったようで、初期は[-3,3]の範囲で探索したとの記述がありました。詳しくはαβ法の解説を参照していただきたいのですが、[-3,3]で探索すると、一方がもう一方より2つ石が多い状況で終局する場合となっても、追加の探索なしで済みます。ただ、論文の著者は途中でもう確実に引き分けになるだろうと思ったのか、前述の[-1,1]の範囲に変更したとのことです。
ステップ分けの真髄をオセロAIの知識を元に考える
※これは論文に明記されていない、私の見解です。
この論文では、おそらくオセロの対局を
- 序盤: 厳密には読み切れないが、ほぼ100%正確な評価値がわかる
- 中盤: 厳密に読み切れなければ、評価値の推測の精度も怪しい
- 終盤: 力技で厳密に読み切れる
の3フェーズに考えています。この序盤が最初の10手(50マス空きまで)で、終盤が最終36マス空き以降だとしたのでしょう。
詳しく解説します。
50マス空きで分割する意味
そもそも、オセロは8x8の64マスの盤面で構成されていて、最初に4つの石が置かれているので60マスの空きがある状態から始まります。また、1手打つごとに1つ石を置くので、空きマスの個数がそのまま残りの手数(パスは1手とカウントしない)となります。つまり、50マス空きというのは、初期局面から10手打った状態のことです。
実は、既存のオセロAI Edax (や、私のEgaroucid) は、序盤10手程度であればミスをすることはほとんどなく、最善手を打ち続けられるだろうという経験的事実があります。これは実際のオセロAI作者としては色々語りたいことがありますがそれは一旦置いておいて、この論文では、この経験的事実を有効に活用したようです。
上で、「推測を用いた探索が間違っていたら、厳密な結果を使いつつ再度推測を使って探索する」と書きました。しかし、序盤10手は上記の経験的事実から、推測を用いた探索を使おうとおそらく推測が外れることはないだろうと思えます。
36マス空きで分割する意味
既存のオセロAIは、初手から60手を完全に読み切る(完全読みする、厳密な最善手を見つける)ことは困難でも、中盤くらい、残り30マス空き程度であれば、かなり簡単に完全読みできます。この論文では、少し頑張って36マス空きは細かい工夫などせず、既存AIで完全読みさせることとしたようです。
では、Algorithm 1で生成できた50マス空きの局面から36マス空きまでの14手はどうするのかというと、それが論文のAlgorithm 5とAlgorithm 6に記されている工夫です。まず、36マス空きの評価値は「多分この値だろう」という評価値にとりあえず決め打って、その評価値を使って探索を継続します。その際、決め打った評価値とその局面はメモしておきます。ここまでがAlgorithm 5です。この決め打ちの探索が終わったら、このメモに含まれる局面を全部厳密に完全読みして、決め打った値と比べます。決め打った評価値と厳密な評価値が全て一致すれば、なんと運の良いことでしょう、50手読みも厳密に正しいと言えます。
ただ、そんな運が良いことはまずないわけで、現実的には、決め打った値と厳密な値が等しくなるまで、決め打ちを使う探索Algorithm 5と、完全読みを行う部分を交互に繰り返します。ここで、決め打ち探索のAlgorithm 5において、36マス空きの局面に遭遇して、すでにその局面の厳密な値が求まっている場合、厳密な値を返すようにします。こうすると徐々に決め打ち探索だったものが厳密なものに近づいていきます。
この工夫には、背景としてAPHIDやADABAなどの分散メモリ環境で並列にゲーム木を探索するアルゴリズムがあるように思えます(論文の関連研究(Related Works)では触れられていませんでしたが)。実際、論文に明記されていないのですが、この部分で最大の工夫は、おそらく分散メモリ環境で独立して探索できるタスクを非常に多く用意したことだと思います。36マス完全読みする局面は大量にあって、それぞれは互いに独立している(と見なせる)ので、完全読みはコンピュータクラスタで簡単に並列実行できます。また、もっと言ってしまえば、前述の50マス空きの局面もいっぱい(後述しますが、2,587個だそう)あるので、これらも同様に簡単に並列実行できます。ゲーム木探索の高速化において最大の難点は並列計算にとことん向かないところですが、この論文ではそれを、オセロのドメイン知識とAPHIDやADABAのような性能の良いアルゴリズムの背景を使って、うまく対処したように見えます。
ちなみに、論文内ではAlgorithm 5を構成するためのサブの擬似コードとして、Algorithm 2から4が書かれています。このことから察する通り、論文自体、なんとなくAlgorithm 5が一番力を入れて書かれていると感じます。私自身もこの論文を読む中で一番知りたかったことはここでした。
Algorithm 1 : 初期局面から10手(50マス空きまで)の浅い探索(推測を使う)をする
論文によると、(対称性を考慮して重複を削除すると)50マス空きの局面は$2,958,551$個あるようです。Algorithm 1では、この$2,958,551$個の局面から、$2,587$個の局面を厳選します。
実は、オセロの初期局面が厳密に引き分けであると求めるために調べなければいけない局面は、$2,958,551$個よりも少なくなります。全ての局面について勝敗を証明しなくても、例えば一部の局面は「黒勝ちか引き分け」、「白勝ちか引き分け」を証明するだけで良かったり(証明すべきものが少しゆるい)、そもそも大多数の局面は勝敗を証明しなくても良かったりします。この性質を使って、予め、計算すべき局面を(証明が必要な局面を予想して)絞っておいたようです。
勝敗を証明すべき局面が減る理由
勝敗を証明すべき局面の数が減るという話は、オセロの弱解決(および、弱解決の根幹アルゴリズムであるαβ法)において非常に重要なものですので、もう少し詳しく説明します。
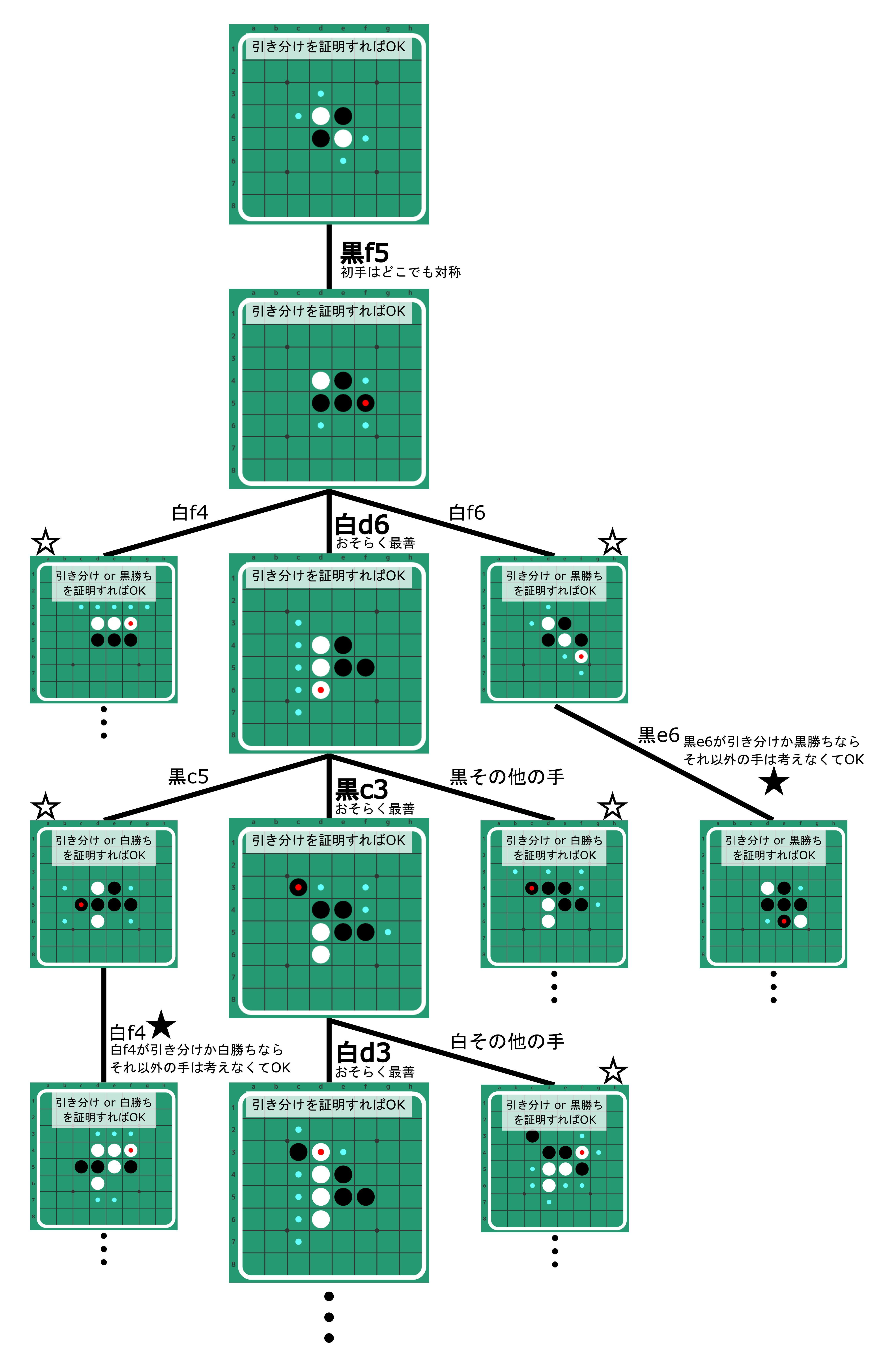
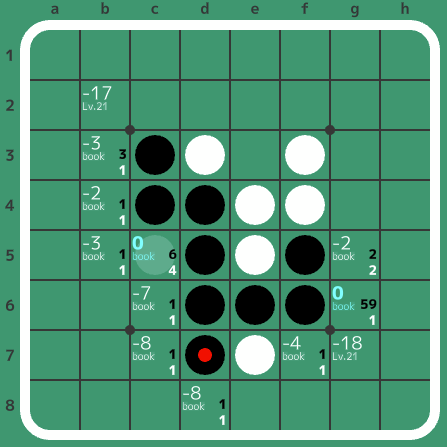
下図に、オセロの開始数手におけるあり得る着手と考えるべき局面のバリエーションと、それぞれの証明すべき事項をまとめてみました。これを例に詳しく解説します。
まず、初手(黒番)は、どこに打っても対称的なので便宜上黒f5(着手の表し方)とします。
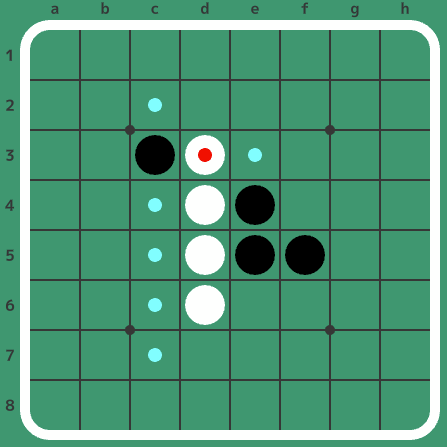
初手を黒f5と打つと、上の局面になります。赤い小さい丸のついた石が直前に打った手で、水色の小さい丸が打てるところです。
2手目(白番)はd6、f4、f6の3通りあります。論文では、最善手(と思しき手)として白d6を選ぶことにしたようです。ちなみに、人間のドメイン知識を使うと、白d6と白f6は両方とも最善(引き分け)だろうと言われていて、白f4は黒勝ちだと言われています。ここで着手によって3種類の局面が出てくるわけですが、実は白f4と白f6の手(画像で☆をつけた局面)については、引き分けまたは黒勝ちを証明するだけでOKです。引き分けを厳密に証明すべきなのは白d6だけで済みます。2手目は白番なので、白d6が引き分けであるならば、その他の手がそれよりも悪い(白負け=黒勝ち)か、引き分けかがわかれば、1手目を打った後の局面(黒f5を打ったところ)が引き分けであることが証明できてしまいます。
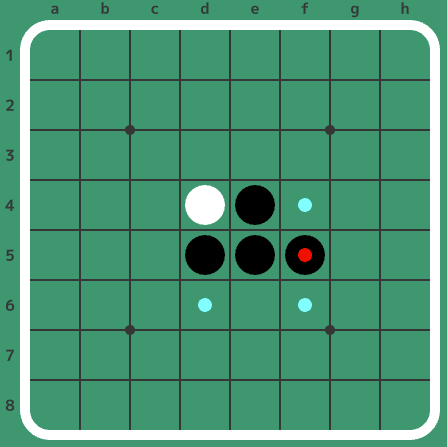
3手目を考えます。まず、初手からf5d6と進んだ局面(下図、黒番)は、2手目でd6を最善手として考えることにしたので、引き分けを証明する必要があります。この局面では黒c3が最善っぽいので、2手目と同じく、黒c3で引き分けを証明し、その他の手は白勝ち(=黒負け)か引き分けを証明します。
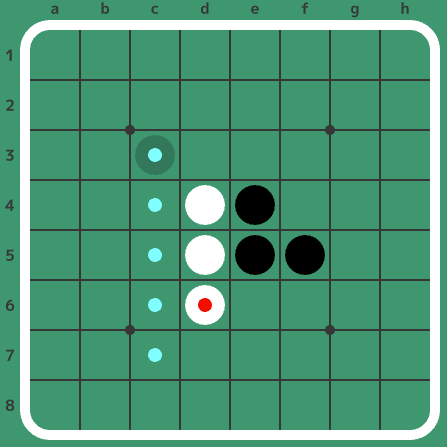
では、同じ3手目で、初手からf5f6と2手進んだ局面(下図、黒番)を考えてみましょう。
この局面は、そもそも2手目の白f6が最善として扱っていない手です(まあ人間のドメイン知識的にはこれも最善と言われていますが)。そのため、この局面はそもそも引き分けか黒勝ちを証明すれば良いのです。この局面では打てる手(黒番)が4つありますが、実はここでは4つのうち1つの手について考えるだけで済みます。選んだ1つの手を黒が打った結果、引き分けか黒勝ちであれば、証明すべきものを満たします。実際には、黒e6(ちなみに人間のドメイン知識では黒e6が唯一の最善で引き分けになります)を選び、その他の手は無視します。選んだe6で引き分けか黒勝ちであることを証明できれば、例えば他に黒d3で黒負けだろうと、弱解決には関係ありません。さらに言えば、もし仮にまた別の黒c4で黒勝ちだったとしても、このf5f6と打った局面が引き分けか黒勝ちであるという結果には影響しません。つまり、こういった「証明すべき内容がゆるい」局面では、最低限証明すべきことを満たす手を打てば、最善手でも若干悪い手でも(例えば勝てる局面で引き分けになる手を打っても)大丈夫です。このような状況が生じる局面に、上の図で★をつけました。
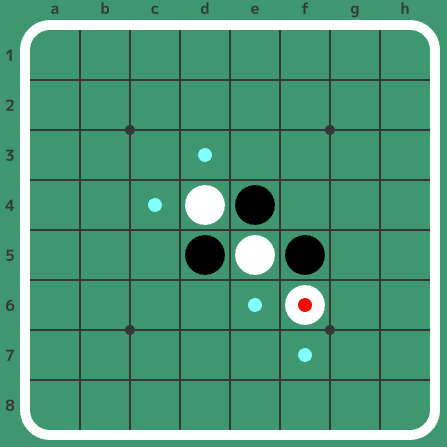
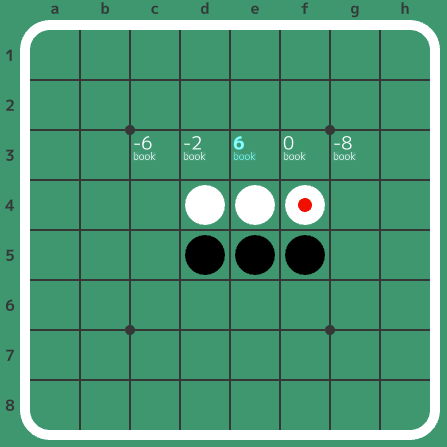
同様に、f5f4から打つ手(3手目)も、引き分けか黒勝ちを証明すれば良いです。下の局面は初手からf5f4と進んだ局面で、打てる手に評価値を表示させてみました。評価値が正の値であればその手番(今回は黒)が勝ち、0なら引き分け、負ならその手番が負けです。数字は最終石差の予想値(+6なら、黒35石、白29石で終局しそう、という意味)です。
黒e3が最善らしいのですが、その他に黒f3が引き分けと思われます。この局面は引き分けか黒勝ちを証明すれば良いので、黒e3と黒f3のどちらを選んでもOKということになります。まあ、普通はe3を選んで黒勝ちを証明すると思いますが…。
さて、ここで一つ概算をしてみましょう。最低限探索しなければいけない木(最小の探索木)は、ざっくり考えると、「黒番では1手しか選ばないが白番では全ての手を確認する木」と、その白黒が逆の「白番では1手しか選ばないが黒番では全ての手を確認する木」の2つをくっつけたものと言えます。さらにざっくり考えて、概算ではこれらの木のそれぞれで重複する部分を無視することにします。10手打った後の到達可能な局面数を$N_{all}=2,958,551$と置きます。そうすると、黒番で1手だけ確認する木の末端のノード数は、$\sqrt{N_{all}}=1,720$程度だと概算できます。この平方根は、オセロが黒白黒白…と交互に打つゲームであることに起因します(パスがあるとこれは成り立ちませんが、これも無視することにします)。白番で1手だけ確認する場合も同じく$1,720$個程度と概算できるので、これを足して合計で$3,440$個程度の局面を見れば良いと概算できます。この概算は本当にざっくりで、実際には各局面での実際の合法手数によって値が増減しますが、論文で述べられた$2,587$個というのは、(オーダーが合っているし)妥当な気がします。
結局Algorithm 1は何をしているのか
さて、本題に戻って、このAlgorithm 1が表す関数が実際に何をしているかと言えば、初手から10手(50マス空き)の探索です。このとき、10手進んだ後のノード(葉ノード)で評価関数が返す評価値として、既存のオセロAI Edax (を改造したもの)を使ったようです。10手打ち進めた後の$2,958,551$個のすべての局面について、それぞれEdaxで10秒ずつ探索させたようです(さらに、引き分けかどうか怪しいような局面はもっと時間をかけて読ませたとのこと)。その結果を推測された評価値として使用しています。この探索を行い、初手から10手ぶんの最小の探索木(と推定されるもの)を求めてしまいます。これは当然、厳密な探索ではありません。ただ、この論文で最終的に述べられているように、この探索木は正しいものであったようです。逆に、ここでの推測が間違っていると大変です。厳密な探索をしてみて推測が間違っていたとなれば、影響する範囲の探索を全部やりなおすことになります。
Algorithm 2-5 : 50マス空きから36マス空きまで14手の浅い探索(推測を使う)をする
ここでは中盤の「ドメイン知識も使えなければ力技で読み切るのもできない」という難しいところを、評価値の推測を使いながらうまく処理します。後述のAlgorithm 6では、Algorithm 5による推測と、既存オセロAIによる完全読みを使った検証をループして、徐々に厳密な結果を求めていきます。なお、この探索手法のアイデアはAPHID (Asynchronous Parallel Hierarchical Iterative Deepening) という既存アルゴリズムが根底にあるだろうと思われます。
なお、私はここについて、Algorithm 1と本質的には同じことをやっていると読み取りました。Algorithm 5は、探索すべき最小の木を構築して、葉ノードとして36マス空きの局面をメモします。ただ、前述の通りドメイン知識を使えないので、Algorithm 1では「ほぼ確実にこれが最善手だろうから、これが最善手ということで探索を進める」と強気だったのが、そうでもなくなってしまいます。そのため、この推測が正しいかを随時検証しつつ、検証結果(厳密に正しい)を使いながら、また推測を行う、ということを繰り返します。
ここでは、Algorithm 5がメインのアルゴリズムです。Algorithm 5を構成するために、Algorithm 2-4があります。
Algorithm 2: 発展させた静的評価関数
この関数は、Edaxの静的評価関数(単に評価関数とも言います)を、少し精度を上げるべく改良したものです。50マス空きから36マス空きの局面において、厳密な評価値を推測するために使われます。
これは、オセロの局面を受け取って、基本的にはEdaxの評価関数にかけて値を返すだけです。ただ、Edaxの評価関数にかけた結果、接戦に近そうな局面であったら、Edaxによって2手読みをさせて少し評価精度を上げた結果を返します。
接戦に近そうな局面かどうかの場合分けや、Edaxによる2手読み時の細かな処理など、精度を担保した上での高速化の工夫が見られます。ちなみにここが1手でなく2手なのは、確か将棋で偶数手読みと奇数手読みの評価値のバラつき方についての研究があったはずで、それを参考にしていると思われます。
少し工夫をしているとは言え、結構誤差の大きそうな評価関数です。50マス空きの局面ではEdaxに10秒間という長い時間読ませていたのに比べて、かなり簡素です。このことから、50マス空きから36マス空きは、推測が外れても致命的な結果にはなりにくく、推測の精度を上げるよりは早く探索を終わらせて推測結果の検証を行うようにした方が効率的だ、という判断のように感じます。
Algorithm 3: 局面の厳密な評価値の存在する範囲を求める
この関数は、50マス空きから36マス空きまでの局面を受け取って、その局面の厳密な評価値が存在する範囲を返します。この範囲は、以前の(厳密な)探索の結果を使って求められる、一番狭い範囲です。
与えられた局面の評価値を推定するに当たって、もしかしたら過去の探索の結果から、その局面の厳密な評価値が存在する範囲がわかっているかもしれません。推定した評価値が、厳密な評価値の存在する範囲を逸脱していたら意味がありませんし、計算の無駄です。また、そもそも計算すべき範囲が絞れるのであれば、無駄な計算を極力省くことができます。これは、そういった無駄な計算を回避するための関数です。
αβ法において、なるべく高速に計算を行うには、探索する範囲(探索窓)を狭めることが有効です(詳しくは基礎知識のαβ法の項目をご覧ください)。
オセロAI Edax (や、私のEgaroucid)で使われている、Enhanced Transposition Cutoffが発想の根底にあると感じました。
Algorithm 4: 36マス空きの局面の評価値を推定する
この関数は、50マス空きから36マス空きまでの局面を受け取って、その局面の評価値の推定値を返す関数です。
まず、受け取った局面から36マス空きに至るまで、αβ法を行います。36マス空き(この探索では、葉ノードとなる)に至ったら、その(36マス空きの局面の)評価値を返します。このとき、厳密な値を参照できるのであれば参照し、使えないのであればAlgorithm 2の評価関数を使った値や、場合によっては適当な値として64を返すようにしてあります。
ちなみにこの場合分けや、厳密な値がわからなかった場合に返す値の64には意味があると思います。が、非常に細かい話なのでいつか追記します。
Algorithm 5: 評価値決め打ちで探索をしつつ、決め打ちで探索した局面をメモする
この関数は、50マス空きから36マス空きまでの局面を受け取って、厳密に探索すべき36マス空きの局面(決め打ちで済ませた局面)の集合を生成する関数です。
こちらもまず、受け取った局面から36マス空きに至るまで、αβ法を行います。このときの手の並び替え(move ordering)にて、Algorithm 3が使用されます。
36マス空きに至ったら、Algorithm 4を実行して、評価値(の推定値)を得ます。このとき、この36マス空きの局面が、すでに厳密に解き終わっているものでなかったら、「決め打ちで値を決めた局面」としてメモを行います。このメモした局面を、後で既存のオセロAI Edaxの改良版によって厳密に探索します。
Algorithm 6 : 浅い探索と厳密な終盤探索を交互に繰り返し、浅い探索の結果を厳密なものであると証明する
ここでは、50マス空きの局面1つを完全読みします。
実はこのアルゴリズムは単純です。Algorithm 5によって発生した「とりあえず評価値決め打ちで対処した局面」の集合を、既存のオセロAI Edaxの改良版を使って全部完全読みします。その結果をメモとして残して、またAlgorithm 5を走らせます。このようなループをずっと繰り返せば、いつかAlgorithm 5を実行したとき「評価値が欲しい全ての局面について、厳密な評価値がメモに残されている」という状況が発生します。こうなれば、晴れて最初の50マス空きの局面が完全読みできたことになります。つまり、50マス空き、50手読みが厳密にできたことになります。
この50マス空き完全読みを、前述の2,587個の全ての局面において行って、なおかつ50マス空きの局面を生成したときにEdaxの中盤探索で決め打ちした値が寸分の違いもなく正確であれば、なんと、60マス空きの初期局面の評価値が厳密に求まったことになります。これが弱解決です。
この論文では、弱解決のために合計で$1.5\times10^{18}$個の局面を探索したと書かれていました。かなりの多さです。また、36マス空きの局面は結局$1.5\times10^9$個生成したそうです。
5. Discussion and Conclusions : 結果の吟味と展望などの解説
ここでは、論文の最後に書いてあった、この研究の展望や結果の考察について簡単に解説します。
もっとドメイン知識を使うとどうなるか?
この論文を読むに当たって、最初、私は誤読をしていました。それは、最初の10手読みの部分に関してドメイン知識としてbookを使ったのではないか、というものです。ここでbookとは、主に人間がオセロを打つにあたって「この手は良い手なのか、悪いのか」を定量的に判断するため、既存のオセロAIを使って頑張って計算した評価値です。当然、厳密な値ではありませんが、ほぼ100%正しいと言える評価値がいくつも経験的に知られています。結局、この論文ではbookというドメイン知識を使わずにオセロを弱解決したようですが、ここではbookを使用するとどうなるだろうかという点について触れられています。
この論文では、bookを使えば弱解決に必要な計算はもっと減らせるであろうと書かれています。私も大いにそう思います。
Edaxの評価関数の誤差について
この論文では、中盤の探索において、Edaxの評価関数(または2手読みした後の評価値)を、終局結果の予測として用いていました。論文のこの項目では、実験結果から、Edaxの評価関数の精度があまり良くないという点が浮き彫りになったと指摘しています。ちなみに、私もオセロAI開発者として、オセロAIの評価関数には精度的な問題がかなりあると感じています。私自身はそれを解決するための試みをやったりしていますが、それは今回書くべきではないでしょう。
結果が正しいかどうかの吟味
この論文の結果を疑う人に対して(実は私も最初この論文を読んだときはかなり疑っていました…)、この論文の計算結果の妥当性を主張しています。主張している点はECCによるメモリのエラー検査および訂正がメインです。また、もし計算上の(CPUやメモリの)問題があっても、最終的にオセロが引き分けに終わるという結論が覆る可能性が非常に低いと主張しています。
私の感想としては、計算が膨大すぎてそう簡単に追試はできない気がしますが、それはそうと、私自身のオセロAI開発経験と知識や人力オセロの経験から、論文の結果は確かに妥当だと思います。追試、私もできるようならしたいですね…
次に解かれるのはチェスだ
この論文では、最後に「次に解かれるのは(有名なゲームだと)チェスだろう。この研究が将来の情報科学の進歩に貢献することを願っている。」という内容で締めくくられています(完璧な訳ではありません)。
ここからは私のコメントです。チェスは、実は人工知能のハエと言われてきた歴史があります。ハエというとなんだか悪い印象を持たれるかもしれませんが、これは遺伝学がハエを題材に大きく発展したのと同じように、人工知能もチェスを題材に発展してきた歴史がある、という意味です。実際、オセロAIで使われるαβ法はチェスを題材に作られたものです。そういう背景を考えると、なんだか感慨深いものがあります。
実はオセロで人間がコンピュータに負けた1997年は、チェスで人間がコンピュータに負けた年でもあります()。5月にチェスで、8月にオセロで、立て続けに世界チャンピオンが敗れました(もっとも、オセロに関してはその数年前から人間の能力を凌駕していることは確実視されていたようですが)。そういった背景も踏まえると、また一段と熱い感情が込み上げてきます。
チェスは、その複雑さはオセロより上だと言われています。オセロAIを制作している感覚からすると、弱解決でさえまだ当分先な気がします。ただ、こうやってオセロが弱解決された論文を読むと、いつかできてしまうのだろうという謎の確信が芽生えてきます。
感想
私自身、オセロの弱解決の一番乗りを狙っていた経緯があり、正直悔しいです。ただ、非常に面白い論文でした。私の今後の研究にも役立ちそうなことがいっぱい書かれていました。また、この論文を、発表されてからすぐに自力でなんとか読める(もしかしたら解釈を間違えているかもしれませんが…)知識を持てていることは、素直に嬉しいです。まだ私は学部2年(なお2年生をやるのは3回目)で、研究の道のごく最初にいると自覚していますが、今回の論文は自信に繋がりました。
また、論文に誤字がいくつかあったり、割付があまり綺麗でなかったりと、「とりあえず真っ先に出した論文」という雰囲気を感じました。今回の論文は査読に通っていませんので、おそらく近いうちに査読付きでもっと丁寧な論文が発表されると思います(そう勝手に期待しています)。その論文を楽しみに待ちつつ、私は自分の研究と開発を続けます。
オセラーとしての見解
ところで、私自身、実は少しだけ人力オセロを打ちます。ですので、ここでは一人のオセラーとして、この論文の私が感じたことを書いておこうと思います。論文の解説というよりは、ほぼ雑談です。
ただ、私自身は日本オセロ連盟2級の実力ですので、その点ご注意ください。
この論文が人力オセロに与える影響
オセロが双方最善で引き分けだからと言って、特に人力オセロには影響がないと思います。
前述の通り、何年も前からオセロの結論が多分引き分けであろうと言われてきました。しかし、結論が引き分けだからと言って、膨大な数の引き分け進行を人間が覚えるのは不可能か、相当な苦行です。さらに、相手がもし最善以外の手を打ってきて、自分の暗記を外れれば、その時点で思考力勝負が始まります。私は、人力オセロにこの「思考力勝負」という面白さを感じています。いかに相手にとってわかりにくい局面に持っていくか、それが楽しいと感じています。
ですから、今、この「引き分けであろう」が「厳密に引き分けであった」とわかっても、人力オセロの文脈では特になんの影響もないでしょう(もちろん、情報科学の分野から見れば、オセロの弱解決は偉業です)。
1997年、当時のオセロ世界チャンピオンの村上さんは、当時世界最強だったオセロAI Logistelloに6戦6敗しました。昨年、2022年はそれからちょうど四半世紀で、その節目の年にまさに当時の主役の一人、村上さんとお話しする機会がありました。それをもとに私が書いた記事を紹介します。
それから、私はオセロAIが人力オセロを終わらせてしまうのかという不安について問うた。私はオセロAI開発者であると同時に、何よりも、オセロプレイヤーである。自らの技術で自らの趣味を終わらせることは避けたい。
「例えば100m走で人間がロボットに敵わないなんて当然じゃないですか。でも人間はオリンピックで100mを走りますよね。それと同じだと思うんです。」
「それはオセロが近い未来に完全解析(初手から真に最善手を打ち続けた結果を求めること)されたとしてもですか?」
「完全解析されたとしても、何も変わらないと思います。」
村上さんにこう言っていただけると幾分安心する。最後に、私自身がオセロの完全解析を目指しているという話をしたら、応援の言葉をかけてくださった。
そういうわけで、私自身、(最近あまり人力オセロを打っていませんが)オセロを楽しみつつ、オセロAIの開発も継続していこうと思います。一般のパソコンで動くオセロAIには、まだまだ改善できる点が山のようにあります。
最善の棋譜を鑑賞する
このセクションは、完全にオセラー向けです。オセロ用語が説明なしに出てきます。本編とはそこまで関係ないので説明は雑です。ご了承ください。
この論文には、最初に最善進行の棋譜が一つ掲載されています。それは
f5d6c3d3c4f4f6f3e6e7d7c5b6d8c6c7d2b5a5a6a7g5e3b4c8g6g4c2e8d1f7e2g3h4f1e1f2g1b1f8g8b3h3b2h5b7a3a4a1a2c1h2h1g2b8a8g7h8h7h6
です。実際に並べてみました。使用ソフトは自作のEgaroucidです。
コンポスに始まり、12手目c5の最善分岐です。c5の後はb6d8と進みます。その後はわりと普通そうな展開に見えました。
このc8は中割りを量産しそうで怖いと思ってしまうのですが、案外中割りが生まれないようで面白いです。まあf7で良さそうなのですが…
辺の攻防については、上辺が双方C打ち、左辺でストナーが若干香る感じですが、ストナーは爆発しません。
そして、この白b2が意外と切れないラインで面白いです。
このラインは結局黒a3で切って、あとは偶数理論で、双方やることが明確に感じました。
基礎知識
ゲームAI関連、およびオセロの基礎知識をまとめました。この論文や記事を読む助けになるかと思います。
評価値
オセロでは終局結果において、勝ち負けよりも詳しく、「自分の石の数-相手の石の数」を評価します(空きマスがあったら勝者の石数にカウントします)。ですので、オセロの評価値は通常、-64から64までの整数となります(さらに、競技の特性上、厳密な値はこのうちで偶数値しか取りません)。なお、この値が0の場合、自分と相手の石数が同じということで、引き分けになります。
αβ法
αβ法は、ゲーム木探索の一般的な手法の一つです。なお、ゲーム木とは木構造の一種で、ゲームにおいて各プレイヤの打てる手をどんどん展開していったときにできる構造です。
このアルゴリズムは「この局面から自分も相手も最善手を打っていったら結果がどうなるか」を求められます。
αβ法は、minimax法という手法の発展版で、αβ法には枝刈りによって高速に実行できるという利点があります。ただし、この枝刈りは解の厳密性を保証するものです。
詳しくは拙著「オセロAIの教科書」などの解説をご覧ください。
move ordering
αβ法は枝刈りによる高速化を行っていると書きましたが、この枝刈りをどれだけ行えるかは、実は局面を探索する順序によって大きく変わります。つまり、ある局面から、手Aを先に探索すると全然枝刈りが発生しないが、手Bを先に探索しておくと、大量に枝刈りが発生する、というものです。
枝刈りを多く発生させるため、αβ法では合法手を列挙した後、枝刈りを引き起こしそうな手から順番に並び替えて、その順番で着手を試みます。この並び替えがmove orderingです。
詳しくは拙著「オセロAIの教科書」などの解説をご覧ください。
最小の探索木
いくらαβ法で大幅な枝刈りができると言っても、当然それには限度があります。最小でもこれだけの大きさのゲーム木を探索しなければ、問題を解けない、という木が必ず存在します。そのゲーム木を「最小の探索木」と言います。なお、この木については、専門用語として決まったものが存在するわけではなさそうです。
1つの局面に対して約$b$個の合法手があり、深さを$d$まで探索する場合、ゲーム木の大きさは$b^d$となり、最小の探索木の大きさは$\sqrt{b^d}$程度になります。ちなみに、これを言い換えると「αβ法は同じ時間でminimax法の倍の深さまで先読みできる」となります。
弱解決
ゲームを「解く」と言った場合、主に弱解決と強解決の2種類があります。
弱解決はこの論文で題材としているもので、「初手から双方が最善の手を打ち続けたらどういう結果になるかが厳密にわかった」というものです。
それに対して強解決は、「初手から(双方悪手も含め)打ち進めた任意の局面について、その局面から双方が最善の結果を打ち続けるとどうなるかを全部求めた」というものです。
少しわかりにくいのですが、前述の通り、弱解決は「相手が悪手を打った場合の対処法は計算したが、自分が悪手を打った場合の対処法は計算していない」というもので、強解決は「相手が悪手を打った場合も自分が悪手を打った場合も、全ての場合を計算した」というものです。
1つの局面に対して約$b$個の合法手があり、深さを$d$まで探索する場合、弱解決で扱わなければいけない局面は$\sqrt{b^d}$個程度になりますが、強解決だと$b^d$となり、文字通り桁違いです。
着手の表し方
オセロにおいて、各マスには座標が割り当ててあり、着手を表すときにはその座標を表記します。
オセロでは列と行にそれぞれ数字とアルファベットが振られています。列にはaからhのアルファベット、行には1から8の数字が使われており、列と行をあわせて表記することで、マスや着手を表します。
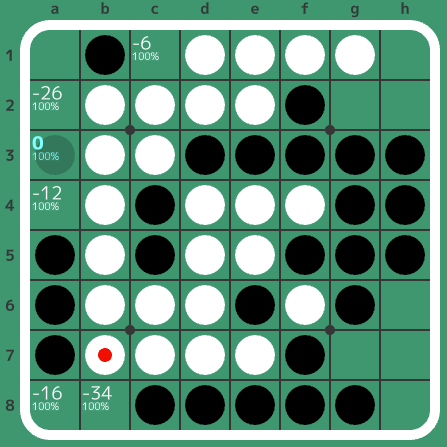
例えば上の画像は(黒番)で、打てる場所(水色の小さい丸がついているマス)はc2、c4、c5、c6、c7、e3の6つです。また、直前に打ったマス(赤い小さい丸がついているマス)はd3です。
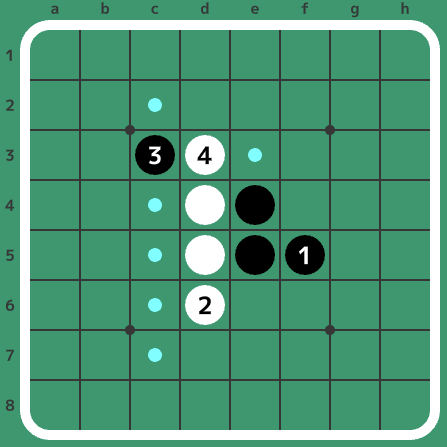
また、着手を連続で書いて棋譜を表すことがあります。例えば上の局面は初手からf5d6c3d3と打った局面です。着手の順番を表示した下図が参考になるかと思います。
更新履歴
2023/11/05 20:23 公開
2023/11/05 21:02 表現を微修正
2023/11/05 23:39 提案手法のポイントを追記、Algorithm 2-5の詳細を追記
2023/11/06 0:36 オセラーとしての見解を追加
2023/11/06 3:19 Algorithm 1についての説明を追加
2023/11/06 3:29 Algorithm 5についての説明を追加
2023/11/06 11:33 表現の修正、基礎知識の執筆
2023/11/06 17:10 誤読していた箇所を修正、全体的に読みやすくなるよう表現を修正
2023/11/06 18:29 結論を引き分けだと決め打った話を追記
2023/11/08 14:19 Discussion and Conclusionsの解説を追記
2023/11/11 10:05 book値への言及が残っていたところを対処(コメントで指摘いただきました、ありがとうございます)
2023/11/12 22:15 手元で10手進んだ局面を全列挙したのでその結果を追記
2023/12/29 21:40 結果を証明すべき局面が減ることについての解説を更新、基礎情報を追加、その他微修正