最近寒いですね。そんなときはパソコンこと「計算もできる暖房」をつけましょう。ポチッ!温風が出てきますね。あったまる~!
ところで、実際のところパソコンってどれくらい暖房としての能力があるんでしょうか…?調べてみましょう。
↑これはCPUのCore i9-13900Kです。今日は暖房として働いてもらいます。
実験装置を作る
暖房能力を調べるために、パソコンによって何かの温度が上昇する様子を測定したいので、熱量計を使います。普通、熱量計は発泡スチロールで水を覆って断熱しつつ水の温度を計測するようなものですが、パソコンを水没させるわけにはいきません。
今回は大きな箱の中でパソコンを動かし、空気を温めることにしました。でもそんな都合の良い箱なんてない……(?)
おや、ここに逸般の誤家庭には大量に在庫があることでおなじみの(?)MDF板があります。
養生テープで適当に貼り付けて箱にしました(ロボット作りなどに使うので穴をあけたりはしたくなく、雑仕様です)。
パソコンと温度計を入れます。パソコンの前方の小さい四角い物体が温度計です。
蓋をします。
完成しました。
前面の一部をアクリル板(転がっていた端材)にしたので蓋を開けずに内部の温度計を目視できます。あと、PCの電源にワットモニターをつけて使用電力を見られるようにしました。テスターは熱電対をつけてサブの温度計として使ってみましたが、数値がガバガバなので「メインの温度計に変な値が出てないかなぁ」と確認するだけの用途としました。
パソコンに負荷をかける
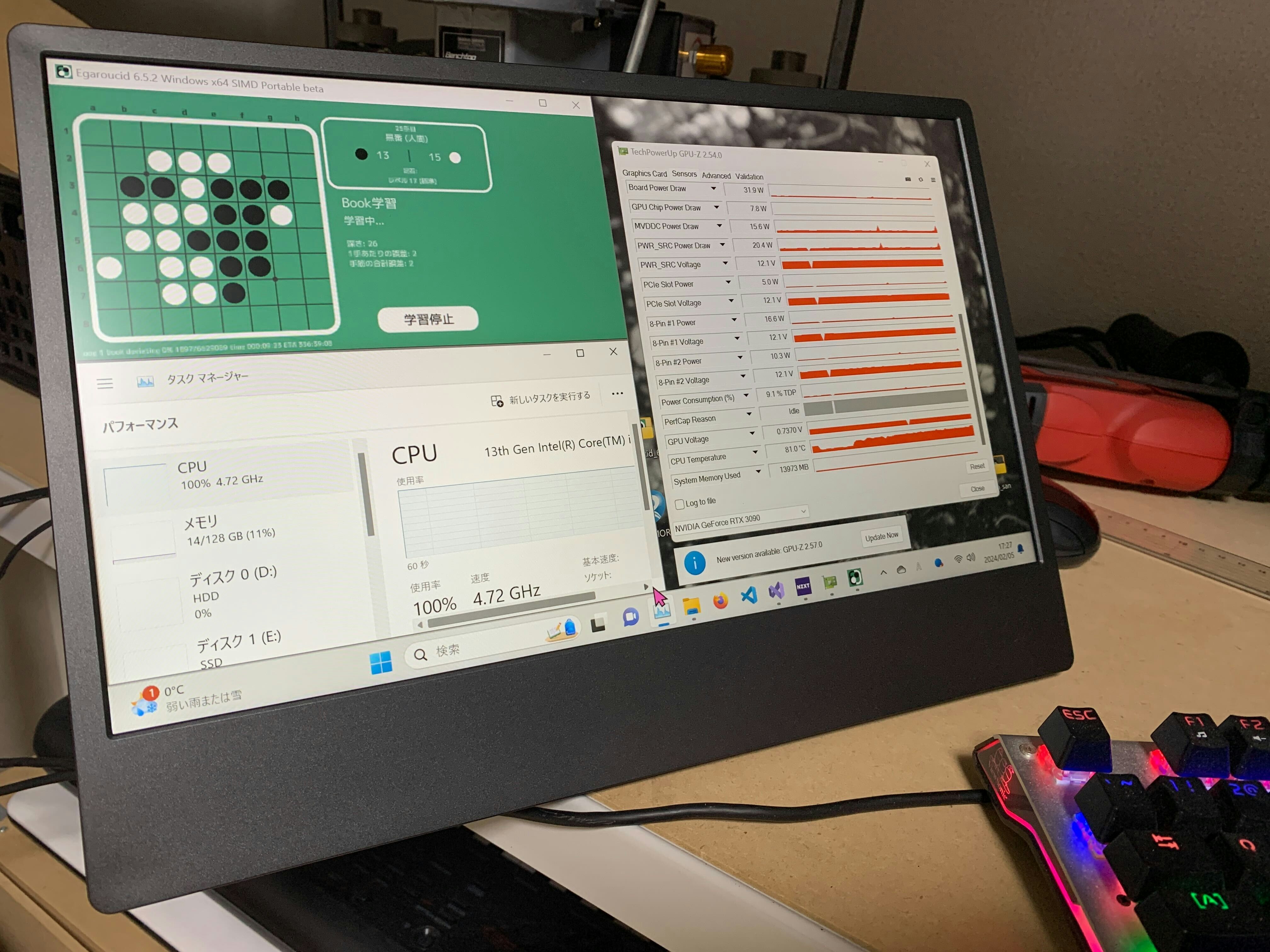
早速パソコンに負荷をかけましょう。とりあえず自作のオセロAI Egaroucidを動かします。
このパソコンのCPUはCore i9-13900Kです。爆熱です。期待できます。
CPU使用率100%、CPU温度は80度を超えました。
お!!!アクリル板越しに温度計を確認すると、室温が21度くらいのところ、27度くらいまで上がっています!(温度計は温風が直撃しない位置に置いています)
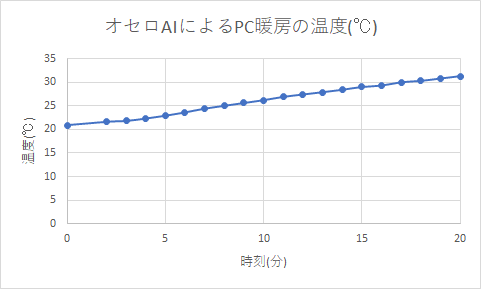
20分間オセロAIを動かし、1分ごとに温度を記録してみました。
20分間で21度から31度まで温度が上がりました!夏!!!!
ちなみに時刻が1分の点は測定を忘れました。さすがに灼熱でパソコンが危険なので、20分経過したところですぐに計算を中止しました。
断熱性能を測定
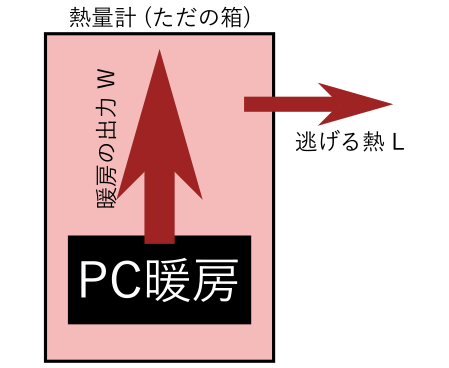
さて、この熱量計ことただの箱、断熱性能が悪いです。オセロAIを動かしていたら外壁がほのかに温かくなりました。これでは正確な暖房性能が測定できません。そこで、この箱の断熱性能を測定しておき、あとでパソコン暖房の性能を計算するときの値の補正に使おうと思いました。
下図において、逃げる熱が無視できないのでこれを考慮することにした、ということです。
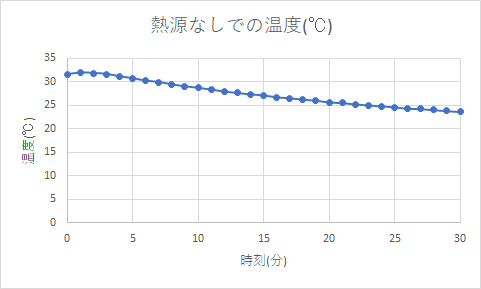
断熱性能の測定のため、オセロAIの計測終了後にパソコンをシャットダウンし、そのまま温度が下がっていく様子を観察しました。30分かけて測定しました。毎分温度計の値を記録したので大変でした。「プログラマーなら自動化しようよ」という気がしますが、そこまでの情熱はありませんでした…
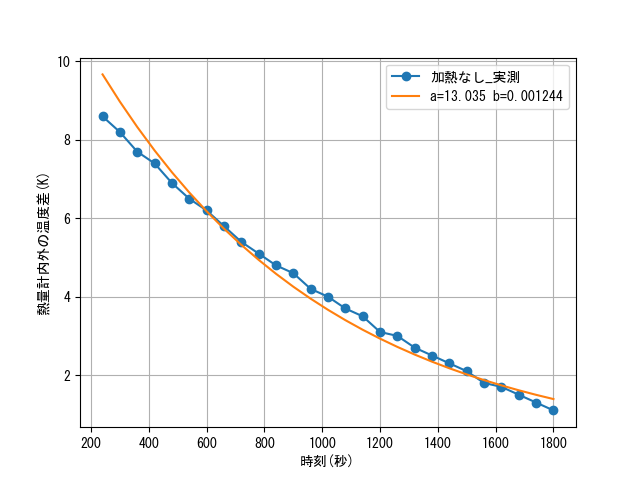
グラフを見ると、徐々に温度が下がっていくのがわかると思います。この結果を使って、この熱量計から熱が逃げる様子をモデル化します。
$L$を単位時間あたりに箱の中から外に出ていく熱量(単位は$\mathrm{W}$)(これを箱内外の温度差の関数として求めたい)とすると、
$$
\frac{\mathrm{d}}{\mathrm{d}t}(T(t)-T_外)=\frac{-L(t)}{C}
$$
という微分方程式が立ちます。ここで、また、箱内部の温度を$T$、外部の温度を$T_外$(定数)、時刻を$t$、箱内の熱容量を$C$としました。
また、単位時間あたりに逃げる熱は箱の内外の温度差に依存するとして、微分方程式を立てます。
$$
\frac{\mathrm{d}}{\mathrm{d}t}(T(t)-T_外)=-b(T(t)-T_外)
$$
$b$は実験に依存する定数です。これを解いて
$$
T(t)-T_外=ae^{-bt}
$$
を満たすように実験結果を近似します。なお、$a$も実験に依存する定数です。箱内外の温度差$T(t)-T_外$を時刻$t$で表すように関数を近似すると、$b=1.24\times10^{-3}$(単位は$\mathrm{s}^{-1}$)とわかりました。近似にはPythonのSciPyを使いました。グラフ表示はMatplotlibです。
なんだか若干合ってない気がしますがまあ良いことにします(最後に原因を考察します)。なお、実験データの最初の方は熱量計内の対流によって値が不正確になっていたので削除してから近似しました。
$a$の妥当性についても考えてみます。$t=0$のときのことを考えると、$T(0)-T_外=a$となるので、$a$はパソコンの電源を落としたときの箱内外の温度差と言えます。実験データのグラフを見ると、室温21度程度に対して箱内の温度は32度程度となっているので、$a=11$程度となるはずでした。ということで、近似によって得られた$a=13$は、まあ妥当だということにします。
さて、ここで先程立てた2つの微分方程式
$$
\frac{\mathrm{d}}{\mathrm{d}t}(T(t)-T_外)=\frac{-L(t)}{C}
$$
と
$$
\frac{\mathrm{d}}{\mathrm{d}t}(T(t)-T_外)=-b(T(t)-T_外)
$$
の右辺同士を等号で繋いで、求めたい$L$について整理して、
$$
L=bC(T(t)-T_外)
$$
を得ます。$b$は求めたので、$L$を求めるために必要なのはあと熱容量$C$のみです。
熱容量は、空気とパソコンの2つに分けて考えます。
空気の熱容量については、箱の容積(からPCの体積を引いたもの)と、空気の比熱から求めます。
箱は各辺大体$450\times900\times600$($\mathrm{mm}$)なので、体積は$V_{箱}=0.243$($\mathrm{m}^3$)です。また、パソコンは各辺大体$220\times480\times400$($\mathrm{mm}$)なので、体積は$V_{PC}=0.0422$($\mathrm{m}^3$)です。よって、空気の体積$V_{空気}=V_箱-V_{PC}=0.201$($\mathrm{m}^3$)とわかりました。
空気の比熱については、ググると$S=1.01\times10^3$($\mathrm{J/(kg・K)}$)程度と出てきます。本当は乾燥空気の値を使うのは良くない気がしますが、面倒なので乾燥空気として扱います。
ただ、このままだと単位が違って熱容量を計算できないので、空気の密度を使います。気圧が1013hPa、気温が22度、湿度が35%程度だったので、空気の密度は$D=1.19$($\mathrm{kg/m^3}$)とわかります。以下のサイトを使いました。
これで箱内の空気の熱容量は$C_{空気}=V_{空気}DS=2.41\times10^2$($\mathrm{J/K}$)とわかりました。
パソコンの熱容量も求めたいです。ただ、パソコンの比熱なんていう数字は誰も知りません。ということで、パソコンの材質をざっくり考えて熱容量を計算しました。
パソコン全体は$12\mathrm{kg}$くらいあります。重いです。そのうち、パソコンケース+その他の骨組みを大体$8\mathrm{kg}$として、この材質を鋼材(比熱は$460\mathrm{J/(kg・K)}$)とします。残りの$4\mathrm{kg}$を基板として、この材質をガラスエポキシ(比熱は$870\mathrm{J/(kg・K)}$程度)とします。
そうすると、パソコンの熱容量$C_{PC}$が求められます。
$C_{PC}=8 \ (\mathrm{kg}) \times 460 \ (\mathrm{J/(kg・K)}) + 4 \ (\mathrm{kg})\times 870 \ (\mathrm{J/(kg・K)}) = 7.16\times10^3 \ (\mathrm{J/K})$
ということで、空気の熱容量とパソコンの熱容量を合計して、熱量計全体の熱容量$C$は
$C=C_{空気}+C_{PC}=7.40\times10^3 \ (\mathrm{J/K})$
です。
実験依存の定数$b$と$C$が求められました。これで以下の式を使って箱から単位時間あたりに流出する熱量$L$が箱内外の温度差で表せました!
$$
L=bC(T(t)-T_外)
$$
若干寄り道です。ここまでの計算で、住宅の断熱性能を表すために使うUA値$(\mathrm{W/(m^2・K)})$(外皮平均熱貫流率)が求められます。UA値は建物内外の温度差が1℃あるときに1秒あたりに逃げる熱量を外皮面積で割ったものです。低ければ低いほど断熱性能が良い(熱を逃がしにくい)ことを表します。せっかくなので求めてみましょう。
まずこの箱(部屋?)の外皮面積を計算します。各辺の大きさが$450\times900\times600$($\mathrm{mm}$)なので、外皮面積$A=2.47$($\mathrm{m^2}$)です。
UA値を計算すると、
$\mathrm{UA値}=\frac{bC}{A}=3.73 \ (\mathrm{W/(m^2・K)})$
でした。
ここで私が住んでいる茨城県で住宅を建設する場合に指標となるUA値は…、0.87(断熱等級4)らしいです。この値が省エネの基準と言われるそうです。住宅ってすごいですね……
CPUの暖房性能を計算する!!
さて、断熱性能を求めたので、これでやっとパソコン暖房の性能を計算できます。
パソコン暖房(Core i9-13900K)を定数値$W$(単位は$\mathrm{W}$)の熱源とします。すると、
$$
\frac{\mathrm{d}}{\mathrm{d}t}(T(t)-T_外)=\frac{W-L(t)}{C}
$$
という微分方程式が立ち、これは断熱性能の実験から$L$を置換して、
$$
T(t)-T_外=\frac{1}{bC}(W-ce^{-bt})
$$
と解けます(新しく出てきた$c$は定数です)。
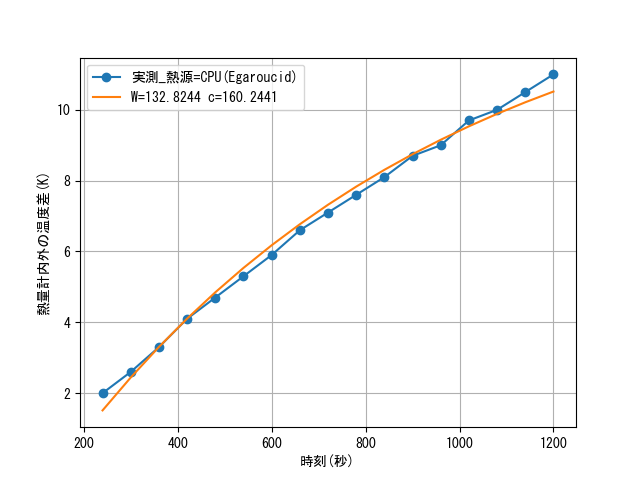
この式を満たすように実験データを近似します。
めでたく$W=133$(W)と求まりました!PCは133Wの暖房になるんですね!!
ちなみに、$t=0$のときを考えると、左辺の$T(t)-T_外$が大体0なはずなので、右辺で$W=c$の関係が期待されます。実際の計算結果は若干$c$が大きいですが、これは$t=0$の決め方が雑だったための誤差と許容できると思います。
実験中のワットモニターは概ね400W程度の値を示していたので、消費電力のうちこの実験で熱として取り出せたのは33%程度らしいです。
GPUの暖房性能も求める・CPUで負荷を変えてみる
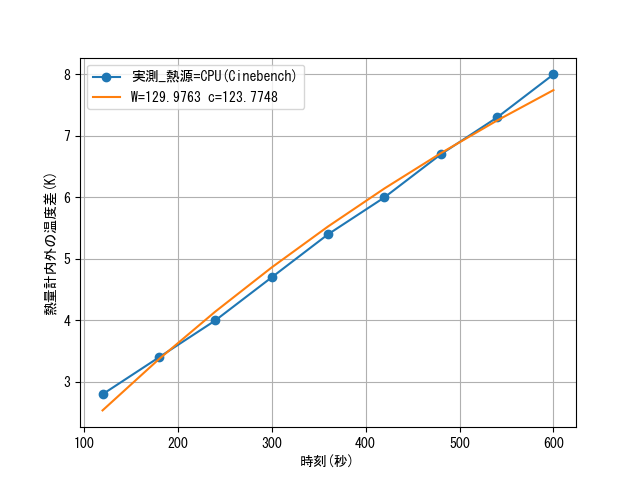
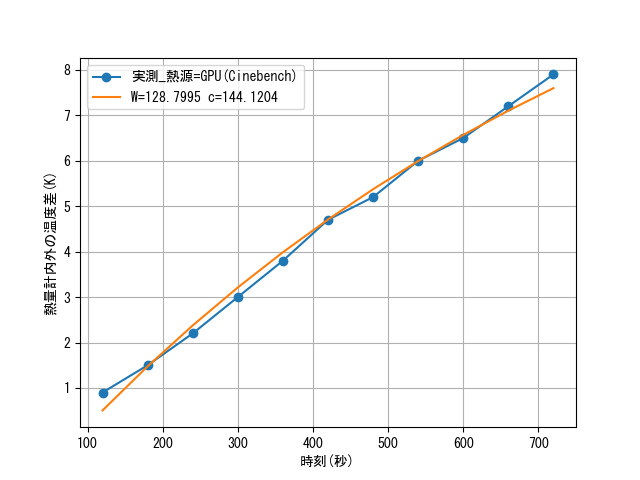
オセロAIによる実験が終わった後、ベンチマークソフトCinebenchによる測定も行ってみました。2024年版はGPUのベンチマークもあるそうで、GPUの暖房性能を見るのにも好都合でした。CPUは変わらずCore i9-13900K、そしてGPUはGeForce RTX3090です。実験方法はオセロAIと同じなので、結果だけ載せます。
CPUでは130W程度、GPUでも129W程度でした。CPUはオセロAIが133Wだったのでだいたい同じ、GPUもたまたまでしょうが、同じくらいでした。ワットモニターによる消費電力はCPUのときに480W程度、GPUのときに450W程度でした。効率はそれぞれ27%、29%程度です。
パソコン暖房の性能まとめ
今回の実験で、PC暖房の性能として以下の数値が求められました。
| 項目 | 出力 | 消費電力 | 効率 |
|---|---|---|---|
| CPU (Egaroucid) | 133W | 400W | 33% |
| CPU (Cinebench) | 130W | 480W | 27% |
| GPU (Cinebench) | 129W | 450W | 29% |
今回の実験では、パソコンを動かすとCPUでもGPUでも130W程度の"出力"が得られることがわかりました。
ということは…、 CPUとGPUの両方をフル活用したら260Wの暖房になるってこと??? とは限らないかもしれませんが、そこそこ暖かそうですね。
今回の実験で使用したCPU Core i9-13900KはTDPが125Wです。CPUを酷使すると130W程度の暖かさを得られたので、TDP程度をそのまま暖房として使えていると解釈できます。
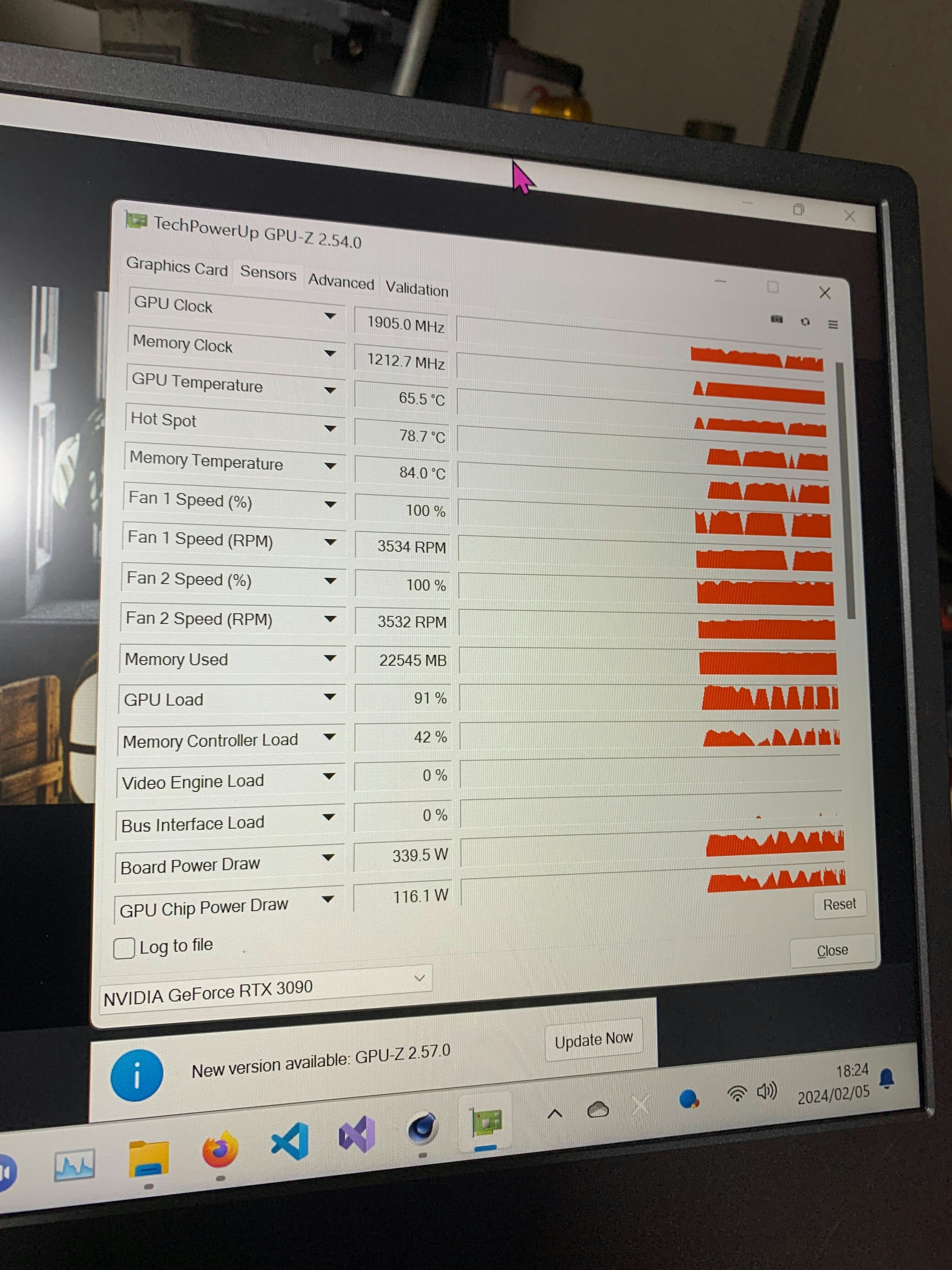
また、GPUとして使用したRTX3090はTDPが350Wですが、Cinebench実行中にGPU-Zでチップの消費電力を見ると116W程度でした。下の画像の一番下、GPU Chip Power Drawです。
GPUの排熱のうち、温風となって出ているものが主にチップの排熱であると仮定すれば、GPUを使用したときに130Wの暖房になるのは、まあ妥当な気がします。
で、普通のエアコンと比べてすごいの?
すごいわけがありません。普通のエアコンは部屋をあたためることに専念している一方、パソコン暖房は部屋をあたためる傍ら、計算をしています。実際、今回の実験ではパソコンから消費電力の30%程度しか熱として取り出せませんでした。今回の実験装置が粗末であるがために効率が悪くなった可能性はありますが、パソコンは熱以外にもファンの回転やGPUの発光(光らなくていいのに…)などにもエネルギーを使っています。それと、ここまで書いておいて言うことではないのですが、プロセッサの開発者は暖房性能を下げる努力をしているはずです(こんなおふざけ実験をしてごめんなさい)。
市販の暖房は今回の実験とは色々条件が違う定義によって性能を表記しているようで、この記事の数値と単純に比較することはできません。さらに、特にエアコンは動作原理が熱交換である関係で、入力した電力に対する暖房性能が非常に高くなるようです(これは記事を書きながら調べていたら初めて知りました。面白いです)。
それでも何か指標がほしいと思って、適当に市販の電気ストーブについて調べると、300Wから1000Wくらいの出力が得られると書いてあるものをちらほら見ました。この値が熱として受け取れる出力そのものなのかはともかく、少なくともパソコン暖房の130W程度よりは数倍暖かそうです。パソコン暖房では寒さをしのげなくなったら、大人しく計算をしない暖房をつけましょう。
値の正確さについて
今回の実験は家にあった材料で雑に一晩で行ったおふざけ実験です。値の正確さについては全く保証しません。計算を間違えている可能性もあります。ご了承ください(もし間違いを発見したら教えていただけると嬉しいです)。
現時点の実験方法の課題としては、対流の影響があります。この実験では空気をあたためることで測定を行いましたが、対流の影響を一切考慮せずに測定してしまったため、温度変化が鈍い可能性があります。実際、理論式によって実験結果を近似すると全体的にカーブがゆるやかな傾向がありました。PCのファンで撹拌されていると踏んだのですが、そうでもないかもしれません。再実験する気はありませんが、小型扇風機でも置くと変わるかもしれませんね…
さらに、今回はパソコンの温風が熱量計の壁に直撃するような構造になっています。これではモデル化した熱の逃げ方を超える勢いで熱が逃げていく可能性が高いです。このあたりもきちんと考慮したかったですね…
極論、400Wの電力を使っているのであれば(音や光に変換されるのは多分そんなに多くないので)、400Wに近い熱が得られてほしい気がします。一応考慮すべきこととして、今回はファンの回転による空気の移動にもエネルギーを使っていると思います。それはどれくらいなんでしょうね…暇だったら概算してみます。それにしても、多分もう少し頑張って精密に実験したり精密に式を立てたりすれば、もう少し熱を受け取れると思います。
余談
この2ヶ月くらい、寒いので暖房を兼ねて自作オセロAIで様々な局面の評価値(形勢)を自動でずっと計算させている(この作業自体、オセロAI開発のためにやっています)のですが、電気代が跳ね上がりました。まあ、そりゃそうですよね…
公開から少しして、計算結果が疑問であるという声をいただきました。元々、考慮する熱容量を全部空気の熱容量として概算していたのですが、改めて計算してみると、今回の実験では空気の熱容量よりもパソコンの熱容量のほうが支配的だということがわかりました。この辺は概算するときに勘が働きませんでした…。ご指摘ありがとうございました。
変更履歴
2024/02/06 公開
2024/02/06 計算部分を大幅に修正。PCの熱容量を加味して大幅に計算結果を変更